





- 2.1 等式性质与不等式性质课件PPT 课件 0 次下载
- 2.2 基本不等式课件PPT 课件 5 次下载
- 2.3 第二课时 一元二次不等式的综合问题课件PPT 课件 0 次下载
- 3.1.1 函数的概念课件PPT 课件 1 次下载
- 3.1.2 第一课时 函数的表示法课件PPT 课件 1 次下载
高中数学人教A版 (2019)必修 第一册第二章 一元二次函数、方程和不等式2.3 二次函数与一元二次方程、不等式课堂教学ppt课件
展开第一课时 一元二次不等式及其解法(一)教材梳理填空1.一元二次不等式:
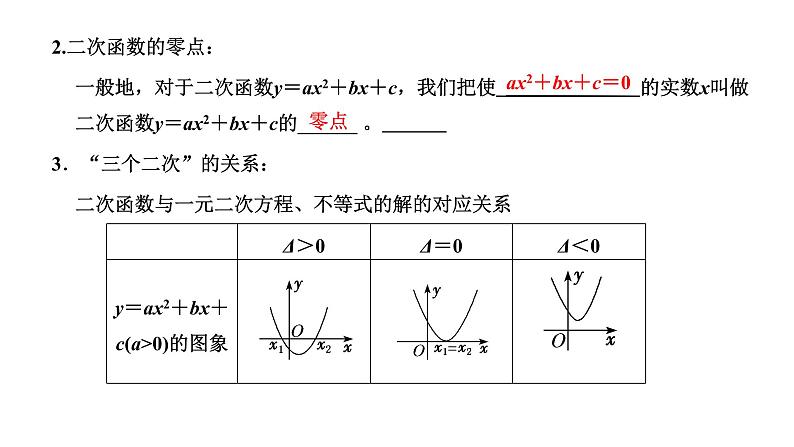
2.二次函数的零点:一般地,对于二次函数y=ax2+bx+c,我们把使 的实数x叫做二次函数y=ax2+bx+c的______ 。 3.“三个二次”的关系:二次函数与一元二次方程、不等式的解的对应关系
{x|x<x1,或x>x2}
{x|x1<x<x2}
[微思考](1)如何理解一元二次不等式中的“一元”与“二次”?提示:“一元”即只含一个未知数,其他元素均为常数(或参数).“二次”即未知数的最高次数必须为2,且其系数不能为0.(2)如何理解一元二次不等式的“解”与“解集”?提示:一元二次不等式的解与一元二次不等式的解集是部分与整体的关系,不要将二者混淆.如1是x2+x>0的一个解,但x2+x>0的解集是一个集合,解集为{x|x<-1或x>0}.
(二)基本知能小试1.判断正误:(1)mx2+5x+3<0是一元二次不等式.( )(2)若不等式ax2+bx+c<0的解集为{x|x1<x<x2}(x1<x2),则必有a>0.( )(3)函数y=ax2+bx+c的零点就是函数图象与x轴的交点.( )(4)若不等式ax2+bx+c>0的解集是{x|x<x1或x>x2}(x1<x2),则方程ax2+bx+c=0的两个根是x1和x2.( )(5)若方程ax2+bx+c=0没有实数根,则不等式ax2+bx+c>0的解集为R.( ) 答案:(1)× (2)√ (3)× (4)√ (5)×
4.若不等式ax2+5x+c>0的解集为{x|2<x<3},则a,c的值分别为________,________.答案:-1 -6
[方法技巧] 解不含参数的一元二次不等式的步骤
【对点练清】1.不等式x(x+2)<3的解集是( )A.{x|-1<x<3} B.{x|-3<x<1}C.{x|x<-1或x>3} D.{x|x<-3或x>1}解析:由题意x(x+2)<3,∴x2+2x-3<0,即(x+3)(x-1)<0,解得-3<x<1,∴该不等式的解集是{x|-3<x<1},故选B.答案:B
题型二 含参数的一元二次不等式的解法【学透用活】[典例2] 解关于x的不等式ax2-(a+1)x+1<0.
[方法技巧] 解含参数的一元二次不等式的步骤
题型三 “三个二次”之间对应关系的应用 【学透用活】“三个二次”之间的关系(1)三个“二次”中,二次函数是主体,讨论二次函数主要是将问题转化为一元二次方程和一元二次不等式的形式来研究.(2)讨论一元二次方程和一元二次不等式又要将其与相应的二次函数相联系,通过二次函数的图象及性质来解决问题,关系如下:
[典例3] 已知关于x的不等式ax2+bx+c>0的解集为{x|2
二、应用性——强调学以致用2.在一个限速40 km/h的弯道上,甲、乙两辆汽车相向而行,发现情况不对,同时刹车,但还是相碰了.事发后现场测得甲车的刹车距离略超过12 m,乙车的刹车距离略超过10 m.又知甲、乙两种车型的刹车距离s m与车速x km/h 之间分别有如下关系:s甲=0.1x+0.01x2,s乙=0.05x+0.005x2.问:超速行驶谁应负主要责任?[析题建模]
高中数学人教A版 (2019)必修 第一册2.3 二次函数与一元二次方程、不等式教课ppt课件: 这是一份高中数学人教A版 (2019)必修 第一册2.3 二次函数与一元二次方程、不等式教课ppt课件,共53页。
高中数学人教A版 (2019)必修 第一册2.3 二次函数与一元二次方程、不等式课文课件ppt: 这是一份高中数学人教A版 (2019)必修 第一册2.3 二次函数与一元二次方程、不等式课文课件ppt,共14页。PPT课件主要包含了无实根,复习引入,复习练习,典型例题,练习巩固,巩固练习等内容,欢迎下载使用。
高中数学人教A版 (2019)必修 第一册第二章 一元二次函数、方程和不等式2.3 二次函数与一元二次方程、不等式课文配套课件ppt: 这是一份高中数学人教A版 (2019)必修 第一册第二章 一元二次函数、方程和不等式2.3 二次函数与一元二次方程、不等式课文配套课件ppt,共17页。PPT课件主要包含了整理得,二次函数有两个零点,x1或6,3由图象得等内容,欢迎下载使用。













