2020-2021学年第29章 直线与圆的位置关系综合与测试同步测试题

这是一份2020-2021学年第29章 直线与圆的位置关系综合与测试同步测试题，共32页。试卷主要包含了将一把直尺等内容，欢迎下载使用。

九年级数学下册第二十九章直线与圆的位置关系定向攻克
考试时间：90分钟；命题人：数学教研组
考生注意：
1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟
2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。
第I卷（选择题 30分）
一、单选题（10小题，每小题3分，共计30分）
1、如图，已知的内接正六边形的边心距是，则阴影部分的面积是（ ）．

A． B． C． D．
2、已知⊙O的半径为3cm，在平面内有一点A，且OA=6cm，则点A与⊙O的位置关系是（ ）
A．点A在⊙O内 ； B．点A在⊙O上；
C．点A在⊙O外； D．不能确定．
3、如图，在矩形ABCD中，，，点O在对角线BD上，以OB为半径作交BC于点E，连接DE；若DE是的切线，此时的半径为（ ）

A． B． C． D．
4、如图，在矩形ABCD中，点E在CD边上，连接AE，将沿AE翻折，使点D落在BC边的点F处，连接AF，在AF上取点O，以O为圆心，线段OF的长为半径作⊙O，⊙O与AB，AE分别相切于点G，H，连接FG，GH．则下列结论错误的是（ ）

A． B．四边形EFGH是菱形
C． D．
5、如图，正六边形螺帽的边长是4cm，那么这个正六边形半径R和扳手的开口a的值分别是（　　）

A．2，2 B．4，4 C．4，2 D．4，
6、在△ABC中，，点O为AB中点．以点C为圆心，CO长为半径作⊙C，则⊙C 与AB的位置关系是（ ）

A．相交 B．相切
C．相离 D．不确定
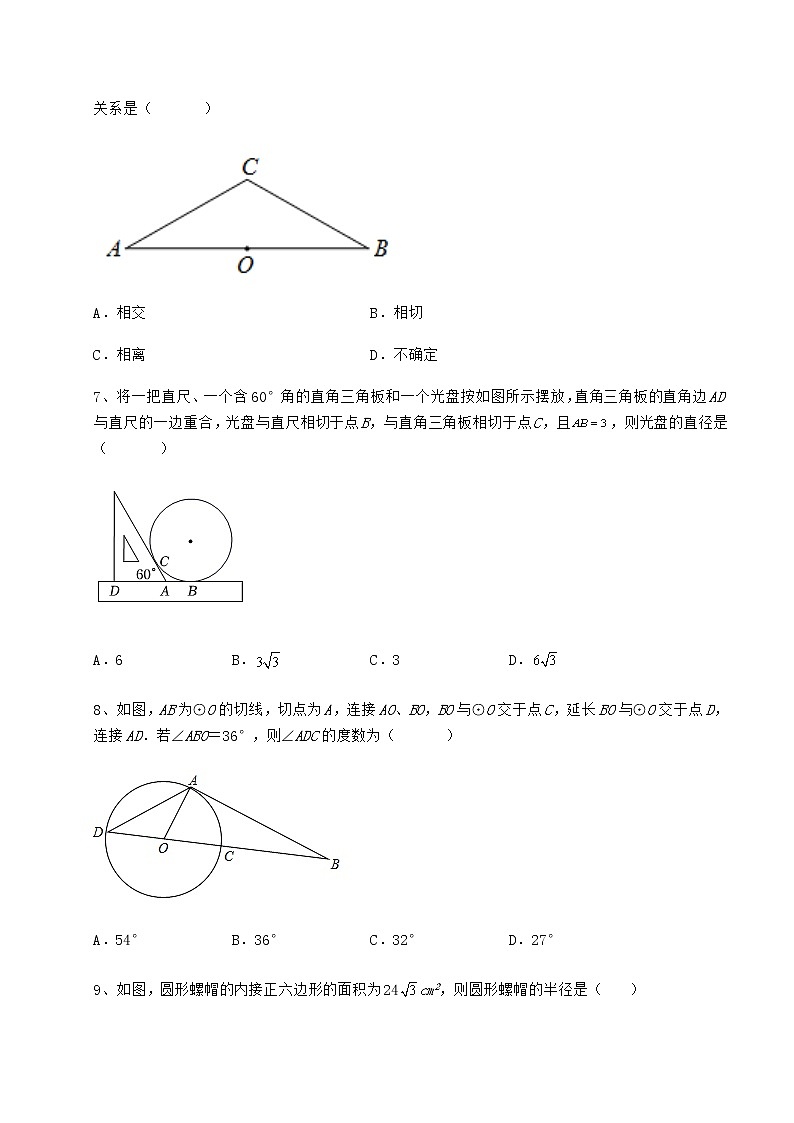
7、将一把直尺、一个含60°角的直角三角板和一个光盘按如图所示摆放，直角三角板的直角边AD与直尺的一边重合，光盘与直尺相切于点B，与直角三角板相切于点C，且，则光盘的直径是（ ）

A．6 B． C．3 D．
8、如图，AB为⊙O的切线，切点为A，连接AO、BO，BO与⊙O交于点C，延长BO与⊙O交于点D，连接AD．若∠ABO＝36°，则∠ADC的度数为（ ）

A．54° B．36° C．32° D．27°
9、如图，圆形螺帽的内接正六边形的面积为24cm2，则圆形螺帽的半径是（　　）

A．1cm B．2cm C．2cm D．4cm
10、的半径为5 ， 若直线与该圆相交， 则圆心到直线的距离可能是 （ ）
A．3 B．5 C．6 D．10
第Ⅱ卷（非选择题 70分）
二、填空题（5小题，每小题4分，共计20分）
1、如图，在⊙O中，AB是⊙O的内接正六边形的一边，BC是⊙O的内接正十边形的一边，则∠ABC＝______°．

2、如图，已知的半径为1，圆心在抛物线上运动，当与轴相切时，圆心的横坐标为______．

3、如图，AB，BC，CD分别与⊙O相切于点E、F、G三点，且AB∥CD，BO＝6，CO＝8，则BE＋GC的长为_____．

4、《九章算术》是我国古代的数学名著，书中有这样的一个问题：“今有勾八步，股十五步，问勾中容圆径几何？”．其意思是：“如图，现有直角三角形，勾（短直角边）长为 8 步，股（长直角边）长为 15 步，问该直角三角形所能容纳的最大圆的直径是多少？”答：该直角三角形所能容纳的最大圆的直径是______步．

5、如图，点O和点I分别是△ABC的外心和内心，若∠BOC＝130°，则∠BIC＝______．

三、解答题（5小题，每小题10分，共计50分）
1、如图，在中，，⊙O是的外接圆，过点C作，交⊙O于点D，连接AD交BC于点E，延长DC至点F，使，连接AF．

(1)求证：；
(2)求证：AF是⊙O的切线．
2、如图，直线MN交⊙O于A，B两点，AC是直径，AD平分∠CAM交⊙O于D，过D作DE⊥MN于E．

(1)求证：DE是⊙O的切线；
(2)若DE＝8，AE＝6，求⊙O的半径．
3、如图，在△ABC中，∠ACB＝90°，AC＝BC，O点在△ABC内部，⊙O经过B、C两点且交AB于点D，连接CO并延长交线段AB于点G，以GD、GC为邻边作平行四边形GDEC．

(1)求证：直线DE是⊙O的切线；
(2)若DE＝7，CE＝5，求⊙O的半径．
4、如图，四边形OAEC是平行四边形，以O为圆心，OC为半径的圆交CE于D，延长CO交O于B，连接AD、AB，AB是O的切线．

(1)求证：AD是O的切线．
(2)若O的半径为4，，求平行四边形OAEC的面积．
5、如图，点E是的内心，AE的延长线交BC于点F，交的外接圆点D．过D作直线．

(1)求证：DM是的切线；
(2)求证：；
(3)若，，求的半径．

-参考答案-
一、单选题
1、D
【解析】
【分析】
连接正六边形的相邻的两个顶点与圆心，构造扇形和等边三角形，则可得到弓形的面积，阴影部分的面积等于弓形的6倍．
【详解】
解：连接、，

，的内接正六边形，
，
∴△DOE是等边三角形，
∴∠DOM=30°，
设，则
，
解得：，
，
根据图可得：，
，
．
故选：D．
【点睛】
本题考查了正多边形与圆及扇形的面积的计算，解题的关键是知道阴影部分的面积等于三个弓形的面积．
2、C
【解析】
【分析】
要确定点与圆的位置关系，主要确定点与圆心的距离与半径的大小关系；利用d＞r时，点在圆外；当d=r时，点在圆上；当d＜r时，点在圆内判断出即可．
【详解】
解：∵⊙O的半径为3cm，OA=6cm，
∴d＞r，
∴点A与⊙O的位置关系是：点A在⊙O外，
故选：C．
【点睛】
本题主要考查了对点与圆的位置关系的判断．关键要记住若半径为r，点到圆心的距离为d，则有：当d＞r时，点在圆外；当d=r时，点在圆上，当d＜r时，点在圆内．
3、D
【解析】
【分析】
设半径为r，如解图，过点O作，根据等腰三角形性质，根据四边形ABCD为矩形，得出∠C=90°=∠OFB，∠OBF=∠DBC，可证．得出，根据勾股定理，代入数据，得出，根据勾股定理在中，，即，根据为的切线，利用勾股定理，解方程即可．
【详解】
解：设半径为r，如解图，过点O作，
∵OB=OE，
∴，
∵四边形ABCD为矩形，
∴∠C=90°=∠OFB，∠OBF=∠DBC，
∴．
∴，
∵，
∴，
∴，
∴，
∴．
在中，，即，
又∵为的切线，
∴，
∴，
解得或0（不合题意舍去）．
故选D．

【点睛】
本题考查矩形性质，等腰三角形性质，圆的切线，勾股定理，一元二次方程，掌握矩形性质，等腰三角形性质，圆的切线性质，勾股定理，一元二次方程，矩形性质，等腰三角形性质，圆的半径相等，勾股定理，一元二次方程，是解题关键．
4、C
【解析】
【分析】
由折叠可得∠DAE=∠FAE，∠D=∠AFE=90°，EF=ED，再根据切线长定理得到AG=AH，∠GAF=∠HAF，进而求出∠GAF=∠HAF=∠DAE=30°，据此对A作出判断；接下来延长EF与AB交于点N，得到EF是⊙O的切线，ANE是等边三角形，证明四边形EFGH是平行四边形，再结合HE=EF可对B作出判断；在RtEFC中，∠C=90°，∠FEC=60°，则EF=2CE，再结合AD=DE对C作出判断；由AG=AH，∠GAF=∠HAF，得出GH⊥AO，不难判断D．
【详解】
解：由折叠可得∠DAE=∠FAE，∠D=∠AFE=90°，EF=ED.
∵AB和AE都是⊙O的切线，点G、H分别是切点，
∴AG=AH，∠GAF=∠HAF，
∴∠GAF=∠HAF=∠DAE=30°，
∴∠BAE=2∠DAE，故A正确，不符合题意；
延长EF与AB交于点N，如图：

∵OF⊥EF，OF是⊙O的半径，
∴EF是⊙O的切线，
∴HE=EF，NF=NG，
∴△ANE是等边三角形，
∴FG//HE，FG=HE，∠AEF=60°，
∴四边形EFGH是平行四边形，∠FEC=60°，
又∵HE=EF，
∴四边形EFGH是菱形，故B正确，不符合题意；
∵AG=AH，∠GAF=∠HAF，
∴GH⊥AO，故D正确，不符合题意；
在Rt△EFC中，∠C=90°，∠FEC=60°，
∴∠EFC=30°，
∴EF=2CE，
∴DE=2CE.
∵在Rt△ADE中，∠AED=60°，
∴AD=DE，
∴AD=2CE，故C错误，符合题意.
故选C.
【点睛】
本题是一道几何综合题，考查了切线长定理及推论，切线的判定，菱形的定义，含30的直角三角形的性质，等边三角形的判定和性质，翻折变换等，正确理解翻折变换及添加辅助线是解决本题的关键．
5、B
【解析】
【分析】
根据正六边形的内角度数可得出∠BAD=30°，为等边三角形，得BC=2AB，再通过解直角三角形即可得出a的值，进而可求出a的值，此题得解．
【详解】
解：如图，

∵正六边形的任一内角为120°，
∴∠ABD=180°-120°=60°，
∴∠BAD=30°，为等边三角形，
∵
∴
∴
∴
∴这个正六边形半径R和扳手的开口a的值分别是4，4．
故选：B．
【点睛】
本题考查了正多边形以及勾股定理，牢记正多边形的内角度数是解题的关键．
6、B
【解析】
【分析】
根据等腰三角形的性质，三线合一即可得，根据三角形切线的判定即可判断是的切线，进而可得⊙C 与AB的位置关系
【详解】
解：连接,

，点O为AB中点．

CO为⊙C的半径，
是的切线，
⊙C 与AB的位置关系是相切
故选B
【点睛】
本题考查了三线合一，切线的判定，直线与圆的位置关系，掌握切线判定定理是解题的关键．
7、D
【解析】
【分析】
如图所示，设圆的圆心为O，连接OC，OB，由切线的性质可知∠OCA=∠OBA=90°，OC=OB，即可证明Rt△OCA≌Rt△OBA得到∠OAC=∠OAB，则，∠AOB=30°，推出OA=2AB=6，利用勾股定理求出，即可得到圆O的直径为．
【详解】
解：如图所示，设圆的圆心为O，连接OC，OB，
∵AC，AB都是圆O的切线，
∴∠OCA=∠OBA=90°，OC=OB，
又∵OA=OA，
∴Rt△OCA≌Rt△OBA（HL），
∴∠OAC=∠OAB，
∵∠DAC=60°，
∴，
∴∠AOB=30°，
∴OA=2AB=6，
∴，
∴圆O的直径为，
故选D．

【点睛】
本题主要考查了切线的性质，全等三角形的性质与判定，含30度角的直角三角形的性质，勾股定理，熟知切线的性质是解题的关键．
8、D
【解析】
【分析】
由切线的性质得出∠OAB=90°，由直角三角形的性质得出∠AOB=90°-∠ABO=54°，由等腰三角形的性质得出∠ADC=∠OAD，再由三角形的外角性质即可得出答案．
【详解】
解：∵AB为⊙O的切线，
∴∠OAB＝90°，
∵∠ABO＝36°，
∴∠AOB＝90°﹣∠ABO＝54°，
∵OA＝OD，
∴∠ADC＝∠OAD，
∵∠AOB＝∠ADC+∠OAD，
∴∠ADC＝∠AOB＝27°；
故选：D．
【点睛】
本题考查了切线的性质、直角三角形的性质、等腰三角形的性质以及三角形的外角性质；熟练掌握切线的性质和等腰三角形的性质是解题的关键．
9、D
【解析】
【分析】
根据圆内接正六边形的性质可得△AOB是正三角形，由面积公式可求出半径．
【详解】
解：如图，由圆内接正六边形的性质可得△AOB是正三角形，过作于

设半径为r，即OA=OB=AB=r，
OM=OA•sin∠OAB=，
∵圆O的内接正六边形的面积为（cm2），
∴△AOB的面积为（cm2），
即，
，
解得r=4，
故选：D．
【点睛】
本题考查正多边形和圆，作边心距转化为直角三角形的问题是解决问题的关键．
10、A
【解析】
【分析】
根据直线l和⊙O相交⇔d＜r，即可判断．
【详解】
解：∵⊙O的半径为5，直线l与⊙O相交，
∴圆心D到直线l的距离d的取值范围是0≤d＜5，
故选：A．
【点睛】
本题考查直线与圆的位置关系，解题的关键是记住①直线l和⊙O相交⇔d＜r②直线l和⊙O相切⇔d=r③直线l和⊙O相离⇔d＞r．
二、填空题
1、132°
【解析】
【分析】
连接AO、BO、CO，根据AB是⊙O的内接正六边形的一边，可得 ， ，从而得到∠ABO=60°，再由BC是⊙O的内接正十边形的一边，可得 ，BO=CO，从而得到，即可求解．
【详解】
解：如图，连接AO、BO、CO，

∵AB是⊙O的内接正六边形的一边，
∴ ， ，
∴ ，
∵BC是⊙O的内接正十边形的一边，
∴ ，BO=CO，
∴，
∴∠ABC=∠ABO+ ∠CBO=60°+72°=132°．
故答案为：132°
【点睛】
本题主要考查了圆的内接多边形的性质，等腰三角形的性质，熟练掌握圆的内接多边形的性质，等腰三角形的性质是解题的关键．
2、2或或0
【解析】
【分析】
当⊙P与x轴相切时，圆心P的纵坐标为1或-1，根据圆心P在抛物线上，所以当y为±1时，可以求出点P的横坐标．
【详解】
解：当y=1时，有1=-x2+1，x=0．
当y=-1时，有-1=-x2+1，x=．
故答案是：2或或0．
【点睛】
本题考查的是二次函数的综合题，利用圆与x轴相切得到点P的纵坐标，然后代入抛物线求出点P的横坐标．
3、10
【解析】
【分析】
先由切线长定理得到BF＝BE，CF＝CG，BO平分∠ABC，CO平分∠BCD，再证明∠BOC＝90°，然后利用勾股定理计算出BC即可．
【详解】
∵AB，BC，CD分别与⊙O相切于点E、F、G三点，
∴BF＝BE，CF＝CG，BO平分∠ABC，CO平分∠BCD，
∴，，
∴，
∵AB∥CD，
∴∠ABC＋∠BCD＝180°，
∴，
∴∠BOC＝90°，
在Rt△OBC中，∵BO＝6，CO＝8，
∴，
∴BE＋CG＝10．
故答案为：10．
【点睛】
此题考查了切线长定理、切线的性质、勾股定理以及直角三角形的判定与性质．此题难度适中，正确理解切线长定理是解决本题的关键．
4、6
【解析】
【分析】
依题意，直角三角形性质，结合题意能够容纳的最大为内切圆，结合内切圆半径，利用等积法求解即可；
【详解】
设直角三角形中能容纳最大圆的半径为：；
依据直角三角形的性质：可得斜边长为：
依据直角三角形面积公式：，即为；
内切圆半径面积公式：，即为；
所以，可得：，所以直径为：；
故填：6；
【点睛】
本题主要考查直角三角形及其内切圆的性质，重点在理解题意和利用内切圆半径求解面积；
5、122.5°
【解析】
【分析】
如图所示，作△ABC外接圆，利用圆周角定理得到∠A=65°，由于I是△ABC的内心，则∠BIC=180°-∠ABC-∠ACB，然后把∠BAC的度数代入计算即可．
【详解】
解：如图所示，作△ABC外接圆，
∵点O是△ABC的外心，∠BOC=130°，
∴∠A=65°，
∴∠ABC+∠ACB=115°，
∵点I是△ABC的内心，
∴∠IBC+∠ICB=×115°=57.5°，
∴∠BIC=180°﹣57.5°=122.5°．
故答案为：122.5°．

【点睛】
此题主要考查了三角形内心和外心的综合应用，根据题意得出∠IBC+∠ICB的度数是解题关键．
三、解答题
1、 (1)见解析；
(2)见解析
【解析】
【分析】
(1)由AB=AC知∠ABC=∠ACB，结合∠ACB=∠BCD，∠ABC=∠ADC得∠BCD=∠ADC，从而得证；
(2)连接OA，由∠CAF=∠CFA知∠ACD=∠CAF+∠CFA=2∠CAF，结合∠ACB=∠BCD得∠ACD=2∠ACB，∠CAF=∠ACB，据此可知AF∥BC，从而得OA⊥AF，从而得证．
(1)
解：∵，
∴，
又∵，
∴，
∴ ；
(2)
解：如图，连接OA，

∵，
∴，
∴，
∵，
∴，
∴，
∵已知，
∴，
∴，
∴，
∴，
∴AF为⊙O的切线．
【点睛】
本题考查了圆周角定理、垂径定理推论、切线的判定、平行线的判定和性质，熟练掌握切线的判定定理是解题的关键．
2、 (1)见解析
(2)
【解析】
【分析】
（1）连接OD，根据等腰三角形的性质和角平分线定义证得∠ODA＝∠DAE，可证得DO∥MN，根据平行线的性质和切线的判定即可证的结论；
（2）连接CD，先由勾股定理求得AD，连接CD，根据圆周角定理和相似三角形的判定证明△ACD∽△ADE，然后根据相似三角形的性质求解AC即可求解．
(1)
证明：连接OD，
∵OA＝OD，
∴∠OAD＝∠ODA，
∵AD平分∠CAM，∠OAD＝∠DAE，
∴∠ODA＝∠DAE，
∴DO∥MN，
∵DE⊥MN，
∴DE⊥OD，
∵D在⊙O上，
∴DE是⊙O的切线；
(2)
解：∵∠AED＝90°，DE＝8，AE＝6，
∴AD＝＝10，
连接CD，∵AC是⊙O的直径，
∴∠ADC＝∠AED＝90°，
∵∠CAD＝∠DAE，
∴△ACD∽△ADE，
∴，即，
∴AC＝，
∴⊙O的半径是．

【点睛】
本题考查等腰三角形的性质、角平分线的定义、平行线的判定与性质、切线的判定、勾股定理、圆周角定理、相似三角形的判定与性质等知识，熟练掌握相关知识的联系与运用是解答的关键．
3、 (1)见解析
(2)4
【解析】
【分析】
（1）连接OD，根据题意和平行四边形的性质可得DE∥CG，可得OD⊥DE，即可求解；
（2）设⊙O的半径为r，因为∠GOD＝90°，根据勾股定理可求解r，当r＝2时，OG＝5，此时点G在⊙O外，不合题意，舍去，可求解．
(1)
证明：连接OD，

∵∠ACB＝90°，AC＝BC，
∴∠ABC＝45°，
∴∠COD＝2∠ABC＝90°，
∵四边形GDEC是平行四边形，
∴DE∥CG，
∴∠ODE+∠COD＝180°，
∴∠ODE＝90°，即OD⊥DE，
∵OD是半径，
∴直线DE是⊙O的切线；
(2)
解：设⊙O的半径为r，
∵四边形GDEC是平行四边形，
∴CG＝DE＝7，DG＝CE＝5，
∵∠GOD＝90°，
∴OD2+OG2＝DG2，即r2+（7﹣r）2＝52，
解得：r1＝3，r2＝4，
当r＝3时，OG＝4＞3，此时点G在⊙O外，不合题意，舍去，
∴r＝4，即⊙O的半径4．
【点睛】
本题主要考查了平行四边形的性质，切线的性质和判定，勾股定理，熟练掌握切线的判定定理是解决本题的关键．
4、 (1)见解析
(2)32
【解析】
【分析】
（1）连接OD，证明，可得，根据切线的性质可得，进而可得，即可证明AD是O的切线；
（2）根据平行四边形OAEC的面积等于2倍即可求解．
(1)
证明：连接OD．

∵四边形OAEC是平行四边形，
∴，




又∵，

∴，
∵AB与相切于点B，


∴，

又∵OD是的半径，
∴AD为的切线．
(2)
∵

在Rt△AOD中，
∴平行四边形OABC的面积是
【点睛】
本题考查了切线的性质与判定，平行四边形的性质，三角形全等的性质与判定，掌握切线的性质与判定是解题的关键．
5、 (1)见解析
(2)见解析
(3)⊙O的半径为5．
【解析】
【分析】
（1）连接OD交BC于H，根据圆周角定理和切线的判定即可证明；
（2）连接BD，由点E是△ABC的内心，得到∠ABE=∠CBE，∠DBC=∠BAD，推出∠BED=∠DBE，根据等角对等边得到BD=DE；
（3）根据垂径定理和勾股定理即可求出结果．
(1)
证明：连接OD交BC于H，如图，

∵点E是△ABC的内心，
∴AD平分∠BAC，
即∠BAD=∠CAD，
∴，
∴OD⊥BC，BH=CH，
∵DM∥BC，
∴OD⊥DM，
∴DM是⊙O的切线；
(2)
证明：∵点E是△ABC的内心，

∴∠ABE=∠CBE，
∵，
∴∠DBC=∠BAD，
∴∠DEB=∠BAD+∠ABE=∠DBC+∠CBE=∠DBE，
即∠BED=∠DBE，
∴BD=DE；
(3)
解：设⊙O的半径为r，
连接OD，OB，如图，

由（1）得OD⊥BC，BH=CH，
∵BC=8，
∴BH=CH=4，
∵DE=2，BD=DE，
∴BD=2，
在Rt△BHD中，BD2=BH2+HD2，
∴（2）2=42+HD2，解得：HD=2，
在Rt△BHO中，
r2=BH2+（r-2）2，解得：r=5．
∴⊙O的半径为5．
【点睛】
本题考查了三角形的内心，切线的判定与性质，三角形的外接圆与外心，圆周角定理，垂径定理，解决本题的关键是综合运用以上知识．