初中数学冀教版九年级下册第29章 直线与圆的位置关系综合与测试课后作业题

九年级数学下册第二十九章直线与圆的位置关系同步训练

 考试时间：90分钟；命题人：数学教研组

考生注意：

1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟

2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上

3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I卷（选择题  30分）

一、单选题（10小题，每小题3分，共计30分）

1、已知⊙O的半径为5，若点P在⊙O内，则OP的长可以是（　　）

A．4 B．5 C．6 D．7

2、在△ABC中，，点O为AB中点．以点C为圆心，CO长为半径作⊙C，则⊙C 与AB的位置关系是（       ）

A．相交 B．相切

C．相离 D．不确定

3、以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形，则（       ）

A．不能构成三角形 B．这个三角形是等边三角形

C．这个三角形是直角三角形 D．这个三角形是等腰三角形

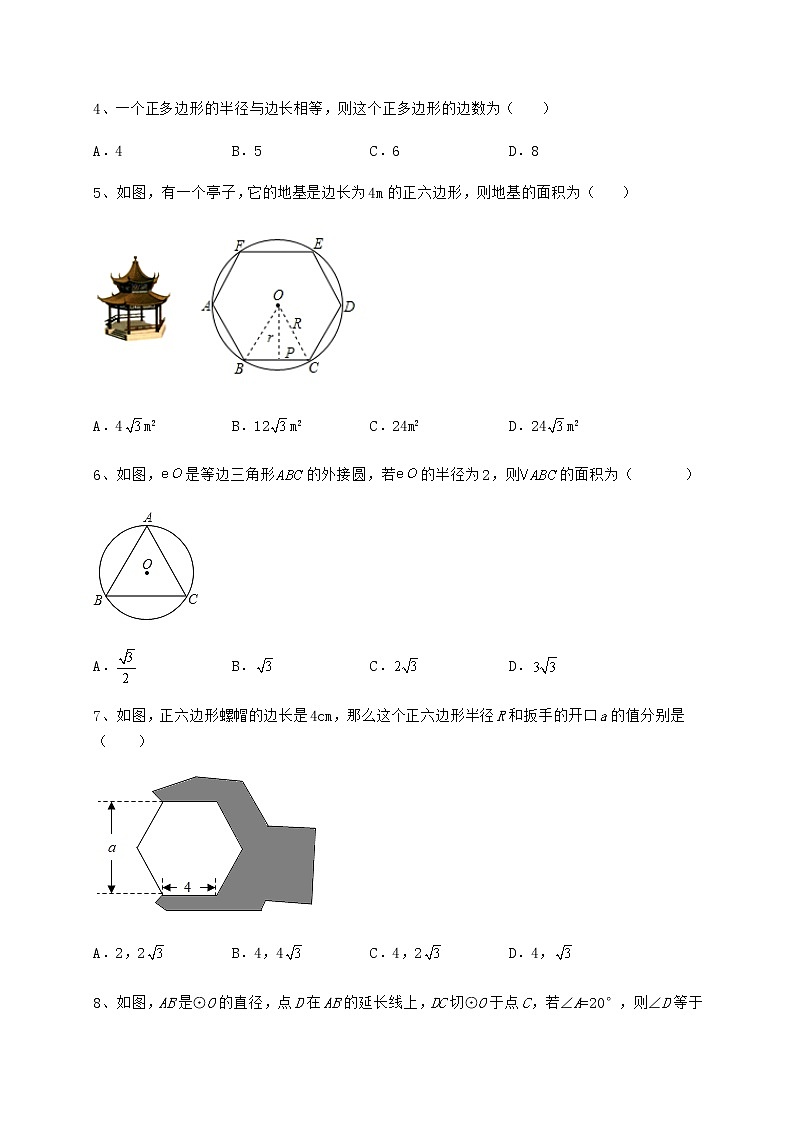
4、一个正多边形的半径与边长相等，则这个正多边形的边数为（　　）

A．4 B．5 C．6 D．8

5、如图，有一个亭子，它的地基是边长为4m的正六边形，则地基的面积为（　　）

A．4m2 B．12m2 C．24m2 D．24m2

6、如图，是等边三角形的外接圆，若的半径为2，则的面积为（       ）

A． B． C． D．

7、如图，正六边形螺帽的边长是4cm，那么这个正六边形半径R和扳手的开口a的值分别是（　　）

A．2，2 B．4，4 C．4，2 D．4，

8、如图，AB是⊙O的直径，点D在AB的延长线上，DC切⊙O于点C，若∠A=20°，则∠D等于（       ）

A．20° B．30° C．50° D．40°

9、如图，与相切于点，连接交于点，点为优弧上一点，连接，，若，的半径，则的长为（       ）

A．4 B． C． D．1

10、如图，已知的内接正六边形的边心距是，则阴影部分的面积是（       ）．

A． B． C． D．

第Ⅱ卷（非选择题  70分）

二、填空题（5小题，每小题4分，共计20分）

1、如图，已知PA、PB是⊙O的两条切线，点A、点B为切点，线段OP交⊙O于点M．下列结论：①PA＝PB；②OP⊥AB；③四边形OAPB有外接圆；④点M是△AOP外接圆的圆心．其中正确的结论是_____（填序号）．

2、如图，在矩形中，是边上的点，经过，，三点的与相切于点．若，，则的半径是__________．

3、如图，AB是⊙O的切线，A为切点，连结OA、OB．若OA＝5，AB＝6，则tan∠AOB＝______．

4、如图，、分别与相切于A、B两点，若，则的度数为________．

5、已知正三角形的边心距为，则正三角形的边长为______．

三、解答题（5小题，每小题10分，共计50分）

1、如图，已知是的直径，点在上，点在外．

(1)动手操作：作的角平分线，与圆交于点（要求：尺规作图，不写作法，保留作图痕迹）

(2)综合运用，在你所作的图中．若，求证：是的切线．

2、如图，直线MN交⊙O于A，B两点，AC是直径，AD平分∠CAM交⊙O于D，过D作DE⊥MN于E．

(1)求证：DE是⊙O的切线；

(2)若DE＝8，AE＝6，求⊙O的半径．

3、如图，△ABC内接于⊙O，AB是⊙O的直径，直线l与⊙O相切于点A，在l上取一点D使得DA=DC，线段DC，AB的延长线交于点E．

(1)求证：直线DC是⊙O的切线；

(2)若BC=4，∠CAB=30°，求图中阴影部分的面积（结果保留π）．

4、如图，在中，，平分，与交于点，，垂足为，与交于点，经过，，三点的与交于点．

(1)求证是的切线；

(2)若，，求的半径．

5、如图，在平面直角坐标系中，，的半径为1．如果将线段绕原点逆时针旋转后的对应线段所在的直线与相切，且切点在线段上，那么线段就是⊙C 的“关联线段”，其中满足题意的最小就是线段与的“关联角”．

(1)如图1，如果线段是的“关联线段”，那么它的“关联角”为______．

(2)如图2，如果、、、、、．那么的“关联线段”有______（填序号，可多选）．

①线段；②线段；③线段

(3)如图3，如果、，线段是的“关联线段”，那么的取值范围是______．

(4)如图4，如果点的横坐标为，且存在以为端点，长度为的线段是的“关联线段”，那么的取值范围是______．

-参考答案-

一、单选题

1、A

【解析】

【分析】

根据点与圆的位置关系可得，由此即可得出答案．

【详解】

解：的半径为5，点在内，

，

观察四个选项可知，只有选项A符合，

故选：A．

【点睛】

本题考查了点与圆的位置关系，熟练掌握点与圆的位置关系（圆内、圆上、圆外）是解题关键．

2、B

【解析】

【分析】

根据等腰三角形的性质，三线合一即可得，根据三角形切线的判定即可判断是的切线，进而可得⊙C 与AB的位置关系

【详解】

解：连接,

，点O为AB中点．

CO为⊙C的半径，

是的切线，

⊙C 与AB的位置关系是相切

故选B

【点睛】

本题考查了三线合一，切线的判定，直线与圆的位置关系，掌握切线判定定理是解题的关键．

3、C

【解析】

【分析】

分别计算出正三角形、正方形、正六边形的边心距,后根据勾股定理的逆定理，等腰三角形的判定，等边三角形的判定，三角形构成的条件，判断即可．

【详解】

如图，∵正三角形、正方形、正六边形都内接于半径为1的圆，边心距分别为OC，OE，OG，OA=1，∠AOC=60°，∠AOE=45°，∠AOG=30°，

∴OC=OAcos60°=，OE= OAcos45°=，OG= OAcos30°=，

∵，

∴这个三角形是直角三角形，

故选C．

【点睛】

本题考查了正多边形与圆，特殊角的三角函数，勾股定理的逆定理，熟练掌握正多边形的计算是解题的关键．

4、C

【解析】

【分析】

如图（见解析），先根据等边三角形的判定与性质可得，再根据正多边形的中心角与边数的关系即可得．

【详解】

解：如图，由题意得：，

是等边三角形，

，

则这个正多边形的边数为，

故选：C．

【点睛】

本题考查了正多边形，熟练掌握正多边形的中心角与边数的关系是解题关键．

5、D

【解析】

【分析】

先根据等边三角形的性质求出△OBC的面积，然后由地基的面积是△OBC的6倍即可得到答案

【详解】

解：如图所示，正六边形ABCDEF，连接OB，OC，过点O作OP⊥BC于P，

由题意得：BC=4cm，

∵六边形ABCD是正六边形，

∴∠BOC=360°÷6=60°，

又∵OB=OC，

∴△OBC是等边三角形，

∴，，

∴，

∴，

∴，

故选D．

【点睛】

本题主要考查了正多边形和圆，等边三角形的性质与判定，勾股定理，熟知正多边形和圆的关系是解题的关键．

6、D

【解析】

【分析】

过点O作OH⊥BC于点H，根据等边三角形的性质即可求出OH和BH的长，再根据垂径定理求出BC的长，最后运用三角形面积公式求解即可．

【详解】

解：过点O作OH⊥BC于点H，连接AO，BO，

∵△ABC是等边三角形，

∴∠ABC=60°，

∵O为三角形外心，

∴∠OAH=30°，

∴OH=OB=1，

∴BH=，AH=-AO+OH=2+1=3

∴

∴

故选：D

【点睛】

本题考查了等边三角形的性质、含30°角的直角三角形的性质，熟练掌握等边三角形的性质，并能进行推理计算是解决问题的关键．

7、B

【解析】

【分析】

根据正六边形的内角度数可得出∠BAD=30°，为等边三角形，得BC=2AB，再通过解直角三角形即可得出a的值，进而可求出a的值，此题得解．

【详解】

解：如图，

∵正六边形的任一内角为120°，

∴∠ABD=180°-120°=60°，

∴∠BAD=30°，为等边三角形，

∵

∴

∴

∴

∴这个正六边形半径R和扳手的开口a的值分别是4，4．

故选：B．

【点睛】

本题考查了正多边形以及勾股定理，牢记正多边形的内角度数是解题的关键．

8、C

【解析】

【分析】

连接CO利用切线的性质定理得出∠OCD=90°，进而求出∠DOC=40°即可得出答案．

【详解】

解：连接OC，

∵DC切⊙O于点C，

∴∠OCD=90°，

∵∠A=20°，

∴∠OCA=20°，

∴∠DOC=40°，

∴∠D=90°-40°=50°．

故选：C．

【点睛】

本题主要考查了切线的性质以及三角形外角性质等知识，根据已知得出∠OCD=90°是解题关键．

9、B

【解析】

【分析】

连接OB，根据切线性质得∠ABO=90°，再根据圆周角定理求得∠AOB=60°，进而求得∠A=30°，然后根据含30°角的直角三角形的性质解答即可．

【详解】

解：连接OB，

∵AB与相切于点B，

∴∠ABO=90°，

∵∠BDC=30°，

∴∠AOB=2∠BDC=60°，

在Rt△ABO中，∠A=90°－60°=30°，OB=OC=2，

∴OA=2OB=4，

∴，

故选：B．

【点睛】

本题考查切线的性质、圆周角定理、直角三角形的锐角互余、含30°角的直角三角形性质、勾股定理，熟练掌握相关知识的联系与运用是解答的关键．

10、D

【解析】

【分析】

连接正六边形的相邻的两个顶点与圆心，构造扇形和等边三角形，则可得到弓形的面积，阴影部分的面积等于弓形的6倍．

【详解】

解：连接、，

，的内接正六边形，

，

∴△DOE是等边三角形，

∴∠DOM=30°，

设，则

，

解得：，

，

根据图可得：，

，

．

故选：D．

【点睛】

本题考查了正多边形与圆及扇形的面积的计算，解题的关键是知道阴影部分的面积等于三个弓形的面积．

二、填空题

1、①②③

【解析】

【分析】

根据切线长定理判断①，结合等腰三角形的性质判断②，利用切线的性质与直角三角形的斜边上的中线等于斜边的一半，可判断③，利用反证法判断④．

【详解】

解：如图， 是的两条切线，

故①正确，

故②正确，

是的两条切线，

取的中点，连接，则

∴以为圆心，为半径作圆，则共圆，故③正确，

M是外接圆的圆心，

与题干提供的条件不符，故④错误，

综上：正确的说法是①②③．

故填①②③．

【点睛】

本题属于圆的综合题，主要考查的是切线长定理、三角形的外接圆、四边形的外接圆等知识点，综合运用圆的相关知识是解答本题的关键．

2、##

【解析】

【分析】

连接EO，并延长交圆于点G，在Rt△DEF中求出EF的值，再证明△DEF∽△FGE，然后根据相似三角形的性质即可求解．

【详解】

解：连接EO，并延长交圆于点G，

∵四边形是矩形，

∴CD=，∠D=90°，

∵与相切于点，

∴OE⊥CD，再结合矩形的性质可得：

∴DE=CE=3．

∵，

∴EF=．

∵与相切于点，

∴∠GED=90°．

∵GE是直径，

∴∠GFE=90°，

∴∠DEF+∠GEF=90°，∠EGF+∠GEF=90°，

∴∠DEF=∠EGF．

∵∠D=∠∠GFE=90°，

∴△DEF∽△FGE，

∴，

∴，

∴GE=，

∴的半径是，

故答案为；．

【点睛】

本题考查了矩形的性质，勾股定理，切线的性质，以及相似三角形的判定与性质，熟练掌握相似三角形的判定与性质是解答本题的关键．

3、

【解析】

【分析】

由题意易得∠OAB=90°，然后根据三角函数可进行求解．

【详解】

解：∵AB是⊙O的切线，

∴∠OAB=90°，

在Rt△OAB中，OA＝5，AB＝6，

∴，

故答案为．

【点睛】

本题主要考查三角函数与切线的性质，熟练掌握三角函数与切线的性质是解题的关键．

4、

【解析】

【分析】

根据已知条件可得出，，再利用圆周角定理得出即可．

【详解】

解：、分别与相切于、两点，

，，

，

，

．

故答案为：．

【点睛】

本题考查的知识点是切线的性质以及圆周角定理，掌握以上知识点是解此题的关键．

5、6

【解析】

【分析】

直接利用正三角形的性质得出BO=2DO=2，再由勾股定理求出BD的长即可解决问题．

【详解】

解：如图所示：连接BO，

由题意可得，OD⊥BC，OD=，∠OBD=30°，

故BO=2DO=2．BC=2BD

由勾股定理得，

∴

故答案为：6．

【点睛】

此题主要考查了正多边形和圆，正确掌握正三角形的性质是解题关键．

三、解答题

1、 (1)作图见解析

(2)证明见解析

【解析】

【分析】

（1）如图，以点C为圆心BC为半径画弧交AC于点M；以B、M为圆心，大于为半径画弧，交点为N，连接CN交于点D即可．

（2）连接AD ， ，，，，AB为直径，进而可得AE是的切线．

(1)

解：如图，以点C为圆心BC为半径画弧交AC于点M；以B、M为圆心，大于为半径画弧，交点为N，连接CN交于点D．

(2)

解：连接AD，如图

∵为直径

∴

∵

∴

∴

又∵AB为直径

∴AE是的切线．

【点睛】

本题考查了角平分线的画法，圆周角，切线的判定等知识．解题的关键在于对知识的灵活熟练的运用．

2、 (1)见解析

(2)

【解析】

【分析】

（1）连接OD，根据等腰三角形的性质和角平分线定义证得∠ODA＝∠DAE，可证得DO∥MN，根据平行线的性质和切线的判定即可证的结论；

（2）连接CD，先由勾股定理求得AD，连接CD，根据圆周角定理和相似三角形的判定证明△ACD∽△ADE，然后根据相似三角形的性质求解AC即可求解．

(1)

证明：连接OD，

∵OA＝OD，

∴∠OAD＝∠ODA，

∵AD平分∠CAM，∠OAD＝∠DAE，

∴∠ODA＝∠DAE，

∴DO∥MN，

∵DE⊥MN，

∴DE⊥OD，

∵D在⊙O上，  

∴DE是⊙O的切线；

(2)

解：∵∠AED＝90°，DE＝8，AE＝6，

∴AD＝＝10，

连接CD，∵AC是⊙O的直径，

∴∠ADC＝∠AED＝90°，

∵∠CAD＝∠DAE，

∴△ACD∽△ADE，

∴，即，

∴AC＝，

∴⊙O的半径是．

【点睛】

本题考查等腰三角形的性质、角平分线的定义、平行线的判定与性质、切线的判定、勾股定理、圆周角定理、相似三角形的判定与性质等知识，熟练掌握相关知识的联系与运用是解答的关键．

3、 (1)见解析

(2)

【解析】

【分析】

（1）连接OC，由题意得，根据等边对等角得，，即可得，则，即可得；

（2）根据三角形的外角定理得，又根据得是等边三角形，则，根据三角形内角和定理得，根据直角三角形的性质得，根据勾股定理得，用三角形OEC的面积减去扇形OCB的面积即可得．

(1)

证明：如图所示，连接OC，

∵AB是的直径，直线l与相切于点A，

∴，

∵，，

∴，，

∴，

∴，

∴直线DC是的切线．

(2)

解：∵，

∴，

又∵，

∴是等边三角形，

∴，

在中，，

∴，

∴，

∴，

∴阴影部分的面积=．

【点睛】

本题考查了切线，三角形的外角定理，等边三角形的判定与性质，直角三角形的性质，勾股定理，解题的关键是掌握这些知识点．

4、 (1)见解析

(2)

【解析】

【分析】

（1）连接，利用角平分线的定义和等腰三角形的性质可证，从而，得到，根据切线的判定方法可证是的切线；

（2）证明，利用相似三角形的性质可求的半径．

(1)

证明：连接，

∵，

∴，

∴是直径，是的中点．

∵平分，

∴，

∵，

∴，

∴，

∴．

又∵，

∴，

∴，

又∵经过半径的外端，

∴是的切线．

(2)

解：∵，

∴，

在与中，

，，

∴．

∴，

在中，，，

∴.

设半径为，则，，

即，

∴．

∴的半径为．

【点睛】

本题考查了切线的判定，等腰三角形的性质，平行线的判定与性质，以及相似三角形的判定与性质，掌握切线的判定方法是解（1）的关键，掌握相似三角形的判定与性质是解（2）的关键．

5、 (1)

(2)②，③

(3)

(4)

【解析】

【分析】

（1）作OD与相切，此时所得最小，根据切线的性质可得，再由含角的直角三角形的特殊性质可得，再由勾股定理可得OD长度，判断切点在OD上即可得

（2）根据勾股定理求出各点与原点的距离与最长切线距离比较即可得；

（3）线段BD绕点O的旋转路线的半径为1的上，当OD与相切时，由（1）可得：，根据题意即可确定t的取值范围，得出线段BD是的“关联线段”；

（4）当m取最大值时，M点运动最小半径是O到过点的直线l的距离m，根据题意可得，得出，即为m的最大值；当m取最小值时，作出相应图形，根据题意可得，再由，及点M所在位置，即可确定m的最小值，综合即可得．

(1)

解：如图所示：作OD与相切，

∴，

∵，，

∴，

∴，

∴此时的角度最小，且，

∴切点在线段OD上，

∴OA的关联角为；

(2)

解：如图所示：连接，，，，

∵，，

∴，

∴切点不在线段上，不是的“关联线段”；

∵，，

∴，，

∵，

∴是的“关联线段”；

∵，

∴是的“关联线段”；

(3)

解：，，线段BD绕点O的旋转路线的半径为1的上，

当OD与相切时，

由（1）可得：，

∴当时，线段BD是的“关联线段”，

故答案为：；

(4)

解：如图所示：当m取最大值时，

M点运动最小半径是O到过点的直线l的距离是m，

∵，，

∴，

∴，

∴m的最大值为4，

如图所示：当m取小值时，

开始时存在ME与相切，

∵，，

∴，

∵，及点M所在位置，

∴，

综上可得：，

故答案为：．

【点睛】

题目主要考查直线与圆的位置关系，线段旋转的性质，勾股定理解三角形等，理解题意，作出相应图象是解题关键．