数学九年级下册第29章 直线与圆的位置关系综合与测试课时作业

这是一份数学九年级下册第29章 直线与圆的位置关系综合与测试课时作业，共31页。试卷主要包含了将一把直尺等内容，欢迎下载使用。
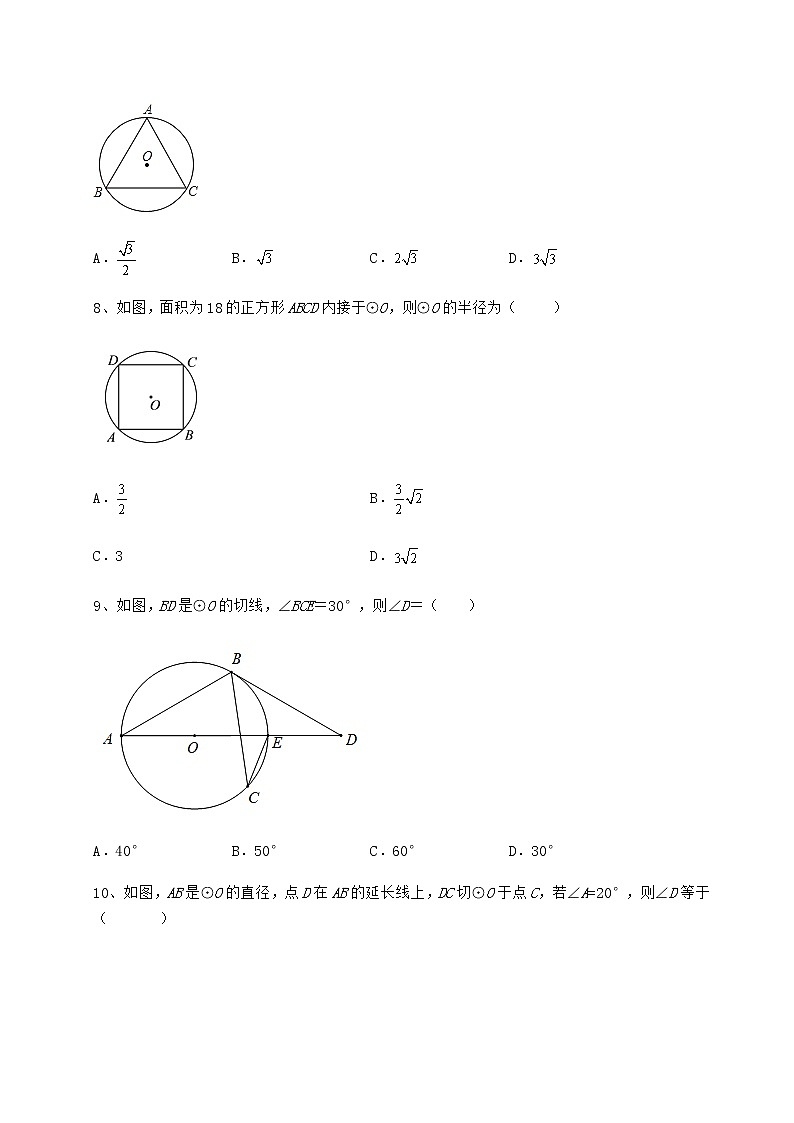
九年级数学下册第二十九章直线与圆的位置关系定向攻克 考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。第I卷（选择题  30分）一、单选题（10小题，每小题3分，共计30分）1、如图，正五边形ABCDE内接于⊙O，则∠CBD的度数是（　　）A．30° B．36° C．60° D．72°2、已知半圆O的直径AB＝8，沿弦EF折叠，当折叠后的圆弧与直径AB相切时，折痕EF的长度m（　　）A．m＝4 B．m＝4 C．4≤m≤4 D．4≤m≤43、如图，与相切于点，连接交于点，点为优弧上一点，连接，，若，的半径，则的长为（       ）A．4 B． C． D．14、已知正三角形外接圆半径为，这个正三角形的边长是（       ）A． B． C． D．5、如图，与相切于点，经过的圆心与交于，若，则（       ）A． B． C． D．6、将一把直尺、一个含60°角的直角三角板和一个光盘按如图所示摆放，直角三角板的直角边AD与直尺的一边重合，光盘与直尺相切于点B，与直角三角板相切于点C，且，则光盘的直径是（       ）A．6 B． C．3 D．7、如图，是等边三角形的外接圆，若的半径为2，则的面积为（       ）A． B． C． D．8、如图，面积为18的正方形ABCD内接于⊙O，则⊙O的半径为（     ）A． B．C．3 D．9、如图，BD是⊙O的切线，∠BCE＝30°，则∠D＝（　　）A．40° B．50° C．60° D．30°10、如图，AB是⊙O的直径，点D在AB的延长线上，DC切⊙O于点C，若∠A=20°，则∠D等于（       ）A．20° B．30° C．50° D．40°第Ⅱ卷（非选择题  70分）二、填空题（5小题，每小题4分，共计20分）1、如图，PA，PB分别与⊙O相切于A，B两点，C是优弧AB上的一个动点，若∠P = 50°，则∠ACB ＝_____________°2、如图，正方形ABCD的边长为4，点E是CD边上一点，连接AE，过点B作BG⊥AE于点G，连接CG并延长交AD于点F，则AF的最大值是_______．3、如图，Rt△ABC中，∠C＝90°，⊙O是△ABC的内切圆，切点为D，E，F，若AD＝5，BE＝12，则△ABC的周长为_____．4、已知正六边形的半径为2，则该正六边形的面积为______°．5、若的半径为5cm，点到圆心的距离为4cm，那么点与的位置关系是__．三、解答题（5小题，每小题10分，共计50分）1、如图，PA，PB是圆的切线，A，B为切点．(1)求作：这个圆的圆心O（用尺规作图，保留作图痕迹，不写作法和证明）；(2)在（1）的条件下，延长AO交射线PB于C点，若AC＝4，PA＝3，请补全图形，并求⊙O的半径．2、如图，是的切线，点在上，与相交于，是的直径，连接，若．(1)求证：平分；(2)当，时，求的半径长．3、如图，是的直径，是圆上两点，且有，连结，作的延长线于点．(1)求证：是的切线；(2)若，求阴影部分的面积．（结果保留）4、如图，已知AB是⊙P的直径，点在⊙P上，为⊙P外一点，且∠ADC＝90°，2∠B＋∠DAB＝180°     (1)试说明：直线为⊙P的切线．(2)若∠B＝30°，AD＝2，求CD的长．5、如图，在中，，⊙O是的外接圆，过点C作，交⊙O于点D，连接AD交BC于点E，延长DC至点F，使，连接AF．(1)求证：；(2)求证：AF是⊙O的切线． -参考答案-一、单选题1、B【解析】【分析】求出正五边形的一个内角的度数，再根据等腰三角形的性质和三角形的内角和定理计算即可．【详解】解：∵正五边形ABCDE中，∴∠BCD==108°，CB=CD，∴∠CBD=∠CDB=（180°-108°）=36°，故选：B．【点睛】本题考查了正多边形和圆，求出正五边形的一个内角度数是解决问题的关键．2、D【解析】【分析】根据题意作出图形，根据垂径定理可得,设，则，分情况讨论求得最大值与最小值，即可解决问题【详解】解：如图，根据题意，折叠后的弧为，为切点，设点为所在的圆心，的半径相等，即，连接，设交于点，根据折叠的性质可得，又则四边形是菱形，且设，则则当取得最大值时，取得最小值，即取得最小值，当取得最小值时，取得最大值，根据题意，当点于点重合时，四边形是正方形则此时当点与点重合时，此时最小，则即则故选D【点睛】本题考查了垂径定理，切线的性质，折叠的性质，勾股定理，分别求得的最大值与最小值是解题的关键．3、B【解析】【分析】连接OB，根据切线性质得∠ABO=90°，再根据圆周角定理求得∠AOB=60°，进而求得∠A=30°，然后根据含30°角的直角三角形的性质解答即可．【详解】解：连接OB，∵AB与相切于点B，∴∠ABO=90°，∵∠BDC=30°，∴∠AOB=2∠BDC=60°，在Rt△ABO中，∠A=90°－60°=30°，OB=OC=2，∴OA=2OB=4，∴，故选：B．【点睛】本题考查切线的性质、圆周角定理、直角三角形的锐角互余、含30°角的直角三角形性质、勾股定理，熟练掌握相关知识的联系与运用是解答的关键．4、B【解析】【分析】如图， 为正三角形ABC的外接圆，过点O作OD⊥AB于点D，连接OA， 再由等边三角形的性质，可得∠OAB=30°，，然后根据锐角三角函数，即可求解．【详解】解：如图， 为正三角形ABC的外接圆，过点O作OD⊥AB于点D，连接OA， 根据题意得：OA= ，∠OAB=30°，，在中， ，∴AB=3，即这个正三角形的边长是3．故选：B【点睛】本题主要考查了锐角三角函数，三角形的外接圆，熟练掌握锐角三角函数，三角形的外接圆性质是解题的关键．5、B【解析】【分析】连结CO，根据切线性质与相切于点，得出OC⊥BC，根据直角三角形两锐角互余∠COB=90°-∠B=90°-40°=50°，然后利用圆周角定理即可．【详解】解：连结CO，∵与相切于点，∴OC⊥BC，∴∠COB+∠B=90°，∵，∴∠COB=90°-∠B=90°-40°=50°，∴．故选B．【点睛】本题考查圆的切线性质，直角三角形两锐角互余性质，圆周角定理，掌握圆的切线性质，直角三角形两锐角互余性质，圆周角定理是解题关键．6、D【解析】【分析】如图所示，设圆的圆心为O，连接OC，OB，由切线的性质可知∠OCA=∠OBA=90°，OC=OB，即可证明Rt△OCA≌Rt△OBA得到∠OAC=∠OAB，则，∠AOB=30°，推出OA=2AB=6，利用勾股定理求出，即可得到圆O的直径为．【详解】解：如图所示，设圆的圆心为O，连接OC，OB，∵AC，AB都是圆O的切线，∴∠OCA=∠OBA=90°，OC=OB，又∵OA=OA，∴Rt△OCA≌Rt△OBA（HL），∴∠OAC=∠OAB，∵∠DAC=60°，∴，∴∠AOB=30°，∴OA=2AB=6，∴，∴圆O的直径为，故选D．【点睛】本题主要考查了切线的性质，全等三角形的性质与判定，含30度角的直角三角形的性质，勾股定理，熟知切线的性质是解题的关键．7、D【解析】【分析】过点O作OH⊥BC于点H，根据等边三角形的性质即可求出OH和BH的长，再根据垂径定理求出BC的长，最后运用三角形面积公式求解即可．【详解】解：过点O作OH⊥BC于点H，连接AO，BO，∵△ABC是等边三角形，∴∠ABC=60°，∵O为三角形外心，∴∠OAH=30°，∴OH=OB=1，∴BH=，AH=-AO+OH=2+1=3∴ ∴ 故选：D【点睛】本题考查了等边三角形的性质、含30°角的直角三角形的性质，熟练掌握等边三角形的性质，并能进行推理计算是解决问题的关键．8、C【解析】【分析】连接OA、OB，则为等腰直角三角形，由正方形面积为18，可求边长为，进而通过勾股定理，可得半径为3．【详解】解：如图，连接OA，OB，则OA=OB，∵四边形ABCD是正方形，∴，∴是等腰直角三角形，∵正方形ABCD的面积是18，∴，∴，即：∴故选C．【点睛】本题考查了正多边形和圆、正方形的性质等知识，构造等腰直角三角形是解题的关键．9、D【解析】【分析】连接，根据同弧所对的圆周角相等，等角对等边，三角形的外角性质可得，根据切线的性质可得，根据直角三角形的两个锐角互余即可求得．【详解】解：连接 BD是⊙O的切线故选D【点睛】本题考查了切线的性质，等弧所对的圆周角相等，直角三角形的两锐角互余，掌握切线的性质是解题的关键．10、C【解析】【分析】连接CO利用切线的性质定理得出∠OCD=90°，进而求出∠DOC=40°即可得出答案．【详解】解：连接OC，∵DC切⊙O于点C，∴∠OCD=90°，∵∠A=20°，∴∠OCA=20°，∴∠DOC=40°，∴∠D=90°-40°=50°．故选：C．【点睛】本题主要考查了切线的性质以及三角形外角性质等知识，根据已知得出∠OCD=90°是解题关键．二、填空题1、【解析】【分析】连接，根据切线的性质以及四边形内角和定理求得，进而根据圆周角定理即可求得∠ACB【详解】解：连接，如图，PA，PB分别与⊙O相切故答案为：【点睛】本题考查了切线的性质，圆周角定理，四边形的内角和，掌握切线的性质是解题的关键．2、1【解析】【分析】以AB为直径作圆，当CF与圆相切时，AF最大．根据切线长定理转化线段AF＋BC＝CF，在Rt△DFC利用勾股定理求解．【详解】解：以AB为直径作圆，因为∠AGB＝90°，所以G点在圆上．当CF与圆相切时，AF最大．此时FA＝FG，BC＝CG．设AF＝x，则DF＝4−x，FC＝4＋x，在Rt△DFC中，利用勾股定理可得：42＋（4−x）2＝（4＋x）2，解得x＝1．故答案为：1．【点睛】本题主要考查正方形的性质、圆中切线长定理以及勾股定理，熟练掌握相关性质定理是解本题的关键．3、40【解析】【分析】利用切线的性质以及正方形的判定方法得出四边形OECD是正方形，进而利用勾股定理得出答案．【详解】解：连接EO，DO，∵⊙O是△ABC的内切圆，切点分别为D，E，F，∴OE⊥BC，OD⊥AC，BF＝BE＝12，AD＝AF＝5，EC＝CD，又∵∠C＝90°，∴四边形ECDO是矩形，又∵EO＝DO，∴矩形OECD是正方形，设EO＝x，则EC＝CD＝x，在Rt△ABC中BC2+AC2＝AB2故（x+12）2+（x+5）2＝172，解得：x＝3(负值已舍)，∴△ABC的周长＝8+15+17＝40．故答案为：40．【点睛】本题主要考查了三角形内切圆与内心，切线长定理，勾股定理，正方形的判定和性质等知识，解题的关键是学会利用参数构建方程解决问题．4、【解析】【分析】正六边形的面积由6个全等的边长为2的等边三角形面积组成，计算一个等边三角形的面积，乘以6即可．【详解】解：设O是正六边形的中心，AB是正六边形的一边，OC是边心距，则△OAB是正三角形．∴OA=AB=2，∴AC=AB=1，∴，∴S△OAB=AB•OC=×2×=，则正六边形的面积为6×=6．故答案为：6．【点睛】本题考查了正多边形的面积，等边三角形的性质，熟练把多边形的面积转化为三角形面积的倍数计算是解题的关键．5、点在圆内【解析】【分析】比较点到圆心的距离d与半径r的大小关系；当时，点在圆外；当时，点在圆上；当时，点在圆内；求值后进行判断即可．【详解】解：的半径为，点A到圆心的距离为点A与的位置关系是：点A在圆内故答案为：点A在圆内．【点睛】本题考查了点与圆的位置关系．解题的关键在于比较点到圆心的距离d与半径r的大小关系．三、解答题1、 (1)见解析；(2)见解析，的半径为【解析】【分析】（1）过点B作BP的垂线，作∠APB的平分线，二线的交点就是圆心；（2）根据切线的性质，利用勾股定理，建立一元一次方程求解即可．(1)如图所示，点O即为所求(2)如图，∵PA是圆的切线，AO是半径，PB是圆的切线，∴∠CAP=90°，PA=PB=3，∠CBO=90°，∵AC=4，∴PC==5，BC=5-3=2，设圆的半径为x，则OC=4-x，∴，解得x=，故圆的半径为．【点睛】本题考查了垂线的画法，角的平分线的画法，切线的性质，切线长定理，勾股定理，一元一次方程的解法，熟练掌握切线的性质，切线长定理和勾股定理是解题的关键．2、 (1)见解析(2)的半径长为．【解析】【分析】（1）根据切线的性质，可得，由平行线的性质，等边对等角，等量代换即可得，进而得证；（2）连接，根据直径所对的圆周角是直角，勾股定理求得，证明列出比例式，代入数值求解可得，进而求得半径(1)证明：如图，连接，∵是的切线，∴，∵，∴，∴，∵，∴，∴，即平分；(2)解：如图，连接，在中，，，由勾股定理得：，∵是的直径，∴，∴，∵，∴，∴，即，解得：，∴的半径长为．【点睛】本题考查了切线的性质，直径所对的圆周角是直角，相似三角形的性质与判定，勾股定理，掌握圆的相关知识以及相似三角形的是解题的关键．3、 (1)见解析(2)【解析】【分析】（1）要证明DE是⊙O的切线，所以连接OD，只要求出∠ODE＝90°即可解答；（2）连接BD，利用Rt△ADB的面积加上弓形面积即可求出阴影部分的面积．(1)证明：连接OD， ∵，∴∠CAD＝∠BAD，∵OA＝OD，∴∠OAD＝∠ODA，∴∠CAD＝∠ODA，∴AE∥OD，∴∠E+∠ODE＝90°，∵DE⊥AC，∴∠E＝90°，∴∠ODE＝180°﹣∠E＝90°，∵OD是圆O的半径，∴DE是⊙O的切线；(2)连接BD， ∵AB是⊙O的直径，∴∠ADB＝90°，∵∠ADE＝60°，∠E＝90°，∴∠CAD＝90°﹣∠ADE＝30°，∴∠DAB＝∠CAD＝30°，∴AB＝2BD，∵，∴∴BD＝2，BA＝4，∴OD＝OB＝2，∴△ODB是等边三角形，∴∠DOB＝60°，∴△ADB的面积＝AD•DB＝×2×2＝2，∵OA＝OB，∴△DOB的面积＝△ADB的面积＝，∴阴影部分的面积为：△ADB的面积+扇形DOB的面积﹣△DOB的面积＝2﹣＝，∴阴影部分的面积为：．【点睛】本题考查了切线的判定与性质，圆周角定理，扇形的面积公式，勾股定理，含30°角的直角三角形，根据题目的已知条件并结合图形，添加适当的辅助线是解题的关键．4、 (1)见解析(2)【解析】【分析】（1）连接PC，则∠APC＝2∠B，可证PC∥DA，证得PC⊥CD，则结论得证；（2）连接AC，根据∠B=30°，等腰三角形外角性质∠CPA=2∠B=60°，再证△APC为等边三角形，可求∠DCA=90°-∠ACP=90°-60°=30°，AD＝2，∠ADC＝90°，利用30°直角三角形性质得出AC=2AD=4，然后根据勾股定理CD=即可．(1)连接PC，∵PC＝PB，∴∠B＝∠PCB，∴∠APC＝2∠B，∵2∠B+∠DAB＝180°，∴∠DAP+∠APC＝180°，∴PC∥DA，∵∠ADC＝90°，∴∠DCP＝90°，即DC⊥CP，∴直线CD为⊙P的切线；(2)连接AC，∵∠B=30°，∴∠CPA=2∠B=60°，∵AP=CP，∠CPA=60°，∴△APC为等边三角形，∵∠DCP=90°，∴∠DCA=90°-∠ACP=90°-60°=30°，∵AD＝2，∠ADC＝90°，∴AC=2AD=4，∴CD=．【点睛】本题考查切线的判定、平行线判定与性质，勾股定理、等腰三角形性质，外角性质，等边三角形的判定与性质等知识，解题的关键是灵活应用这些知识解决问题．5、 (1)见解析；(2)见解析【解析】【分析】(1)由AB=AC知∠ABC=∠ACB，结合∠ACB=∠BCD，∠ABC=∠ADC得∠BCD=∠ADC，从而得证；(2)连接OA，由∠CAF=∠CFA知∠ACD=∠CAF+∠CFA=2∠CAF，结合∠ACB=∠BCD得∠ACD=2∠ACB，∠CAF=∠ACB，据此可知AF∥BC，从而得OA⊥AF，从而得证．(1)解：∵，∴，又∵，∴，∴ ；(2)解：如图，连接OA， ∵，∴，∴，∵，∴，∴，∵已知，∴，∴，∴，∴，∴AF为⊙O的切线．【点睛】本题考查了圆周角定理、垂径定理推论、切线的判定、平行线的判定和性质，熟练掌握切线的判定定理是解题的关键．