初中数学湘教版八年级下册2.5.1矩形的性质教案配套ppt课件

这是一份初中数学湘教版八年级下册2.5.1矩形的性质教案配套ppt课件，共17页。PPT课件主要包含了新课导入，点击打开，矩形的定义，矩形的性质，∴ACDB，平行四边形和矩形对比，由勾股定理得，随堂练习等内容，欢迎下载使用。

在小学，我们初步认识了长方形，你能举出日常生活中有关长方形的例子吗？
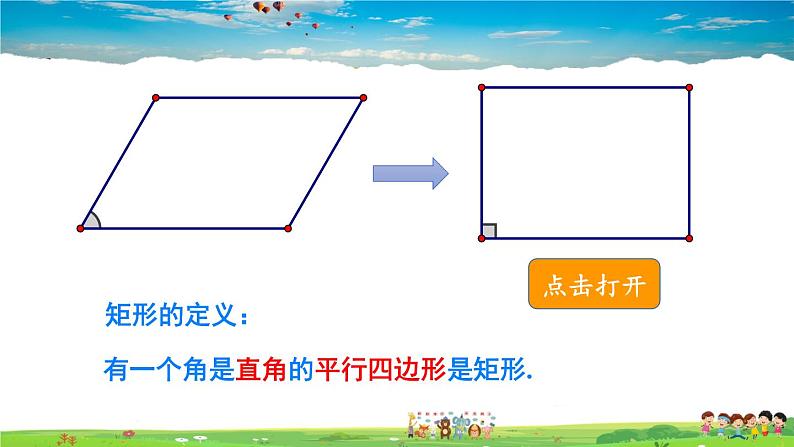
观察图中的长方形，它是平行四边形吗？它有什么特点呢？
有一个角是直角的平行四边形是矩形.
因为矩形是平行四边形，所以它具有平行四边形的所有性质. 由于它有一个角为直角，它是否具有一般平行四边形不具有的一些性质呢？
如图，四边形 ABCD 为矩形，那么对角线 AC 与 DB 相等吗？
证明：四边形 ABCD 是矩形，于是有AB = DC，∠ABC = ∠DCB = 90°，BC = CB.
∴△ABC ≌ △DCB (SAS).
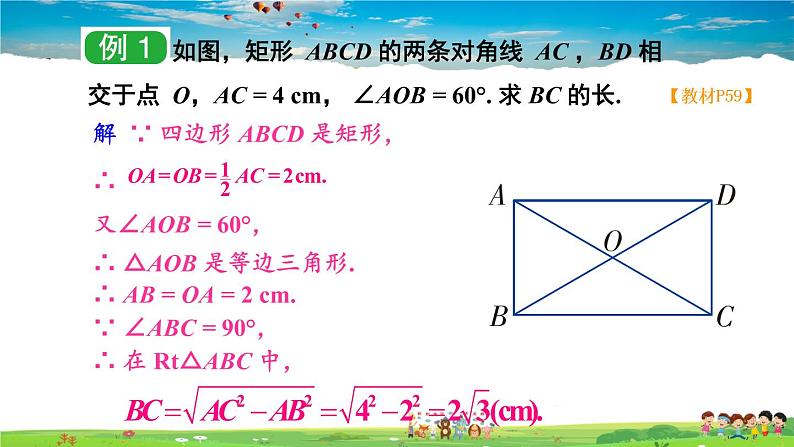
如图，矩形 ABCD 的两条对角线 AC ，BD 相交于点 O，AC = 4 cm， ∠AOB = 60°. 求 BC 的长.
∴ △AOB 是等边三角形.
∴ AB = OA = 2 cm.
又∠AOB = 60°，
∵ ∠ABC = 90°，
解 ∵ 四边形 ABCD 是矩形，
∴ 在 Rt△ABC 中，
在纸上画一个矩形 ABCD，把它剪下来，怎样折叠能使矩形在折痕两旁的部分互相重合？满足这个要求的折叠方法有几种？由此猜测：矩形是轴对称图形吗？如果是，它有几条对称轴？你的猜测正确吗？
阅读课本P60，进一步理解为什么矩形是轴对称图形.
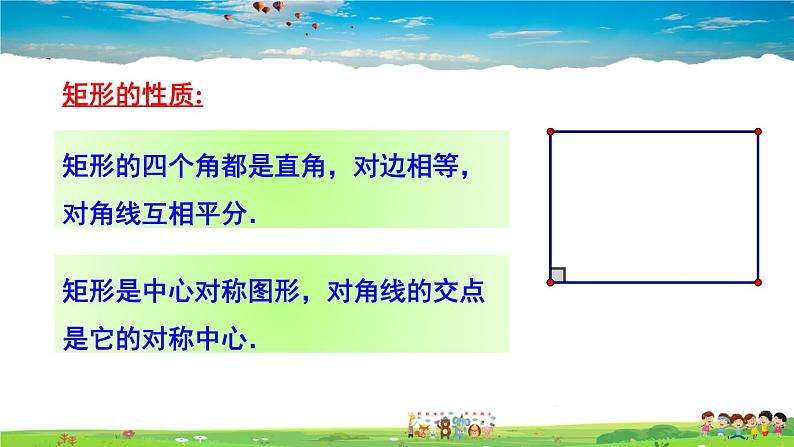
矩形是轴对称图形，过每一组对边中点的直线都是矩形的对称轴.
解：如右图所示，在矩形ABCD中，AC=BD=2cm，∠AOB=60°，
已知矩形的一条对角线的长度为 2 cm，两条对角线的一个夹角为 60°，求矩形的各边长.
∴AO= AC，BO= BD，
∴AO=BO= ×2=1(cm)，
∴△AOB是等边三角形. ∴AB=1cm.
在Rt△ABC中，∠ABC=90°，
∴AD=BC= cm，AB=DC=1cm.
∴矩形的各边长分别为1cm， cm，1cm， cm.
2. 如图，四边形 ABCD 为矩形，试利用矩形的性质说明： 直角三角形 ABC 斜边 AC 上的中线 BO 等于斜边的一半.
解：∵ BD，AC 是矩形 ABCD 的对角线，∴BD = AC. ∴ BO = BD = AC.
即直角三角形ABC斜边AC上的中线BO等于斜边的一半.
1.如图，在矩形 ABCD 中， E 是 AB 上一点，F 是 AD 上一点，EF⊥FC，且 EF = FC，DF = 4 cm，求 AE 的长.
解: ∵ EF ⊥ FC，∴ ∠AFE+∠DFC=90°.又∠DCF+∠DFC=90°，∴ ∠DCF = ∠AFE ．又∠A=∠D=90°，EF=FC，∴Rt△FAE ≌ Rt△CDF．∴AE = DF = 4 cm.
2. 如图，在矩形 ABCD 中，AB ＝ 3 cm， AD ＝ 4 cm，过对角线 BD 的中点 O 作 BD 的垂线 EF，分别交 AD，BC于点 E，F， 求 AE 的长.
解：连接 BE，易得Rt△EOB≌Rt△EOD，∴BE=DE.在Rt△AEB中，AB2+AE2=BE2=DE2，∴32+AE2=(4-AE)2，∴9+AE2=16-8AE+AE2，∴AE = cm.