江苏专用2022版高考数学总复习第一章集合与常用逻辑用语不等式第三节简单的逻辑联结词全称量词与存在量词课件

这是一份江苏专用2022版高考数学总复习第一章集合与常用逻辑用语不等式第三节简单的逻辑联结词全称量词与存在量词课件，共34页。
学习要求:1.了解逻辑联结词“或”“且”“非”的含义.2.理解全称量词与存在量词的意义.3.能正确地对含有一个量词的命题进行否定.
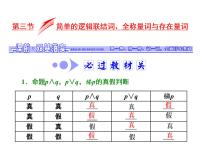
1.简单的逻辑联结词(1)命题中的①　或    、且、非叫做逻辑联结词.(2)命题p∧q、p∨q、¬p的真假判断:
▶提醒    逻辑联结词与集合的关系:“或、且、非”三个逻辑联结词对应着 集合运算中的“并、交、补”,因此,常常借助集合的“并、交、补”的意义 来解答由“或、且、非”三个逻辑联结词构成的命题问题.
2.全称量词与存在量词
3.全称命题和特称命题
4.含有一个量词的命题的否定
▶提醒    含有一个量词的命题的否定的规律是“改量词,否结论”.
知识拓展1.记忆口诀:(1)“p或q”,有真则真;(2)“p且q”,有假则假;(3)“¬p”,真假相反.2.命题p∧q的否定是(¬p)∨(¬q);命题p∨q的否定是(¬p)∧(¬q).
1.判断正误(正确的打“√”,错误的打“✕”).(1)命题“5>6或5>2”是假命题. (　　)(2)p∧q为真的充要条件是p为真或q为真. (　　)(3)“长方形的对角线相等”是特称命题. (　　)(4)命题“菱形的对角线相等”的否定是“菱形的对角线不相等”.(　　)(5)若命题p,q中至少有一个是真命题,则p∨q是真命题. (　　)(6)若命题¬(p∧q)是假命题,则命题p,q中至多有一个是真命题. (　　)
2.(人教A版必修第一册P30例4改编)命题“对任意的x∈R,3x3-2x2+40”为假命题,可知“∀x∈[-1,1],x2+3x+a≤0”为真命题,令g(x)=x2+3x+a,则∀x∈[-1,1],g(x)≤0恒成立,因为g(x)=x2+3x+a图象的对称轴为直线x=- ,所以g(x)在x∈[-1,1]上单调递增,所以只需g(1)≤0即可,即4+a≤0,解得a≤-4,即a∈(-∞,-4].
5.已知命题p:若x>y,则-x ,则xx2　　　　    B.∃x0∈R,lg x0=0C.∀x∈ ,x>sin x　　　　    D.∃x0∈R,sin x0+cs x0= 
5.下列命题为真命题的是 (　　)A.∃x0∈R, ≤x0-2B.∀x∈R,2x>2-x2C.函数f(x)= 是定义域上的减函数D.能“被2整除的整数都是偶数”的否定是“至少存在一个能被2整除的整 数不是偶数”
6.已知a>0,函数f(x)=ax2+bx+c,若x1满足关于x的方程2ax+b=0,则下列选项中的 命题为假命题的是 (　　)A.∃x0∈R, f(x0)≤f(x1)B.∃x0∈R, f(x0)≥f(x1)C.∀x∈R, f(x)≤f(x1)D.∀x∈R, f(x)≥f(x1)
7.命题p:∃x0∈R, ≤0,命题q:∀x∈(0,+∞),x>sin x,其中真命题是　　　    ;命题p的否定是　　　　　　    .
方法技巧1.对全称命题与特称命题进行否定的方法(1)改变量词:确定命题所含量词的类型,省去量词的要结合命题的含义加上 量词,再对量词进行改变.(2)否定结论:对原命题的结论进行否定.
2.全称命题与特称命题的真假判断的方法(1)要判断一个全称命题是真命题,必须对限定集合M中的每个元素x验证p(x) 成立;要判断全称命题是假命题,只要能找出集合M中的一个x=x0,使得p(x0)不 成立即可(这就是通常所说的“举出一个反例”).(2)要判断一个特称命题是真命题,只要在限定集合M中,至少能找到一个x=x0, 使p(x0)成立,否则,这一特称命题就是假命题.▶提醒　因为命题p与¬p的真假性相反.因此无论是全称命题,还是特称命题, 当其真假性不容易正面判断时,可先判断其否定的真假.
典例1　(1)已知命题p:∀x∈R,2x0;命题q:“x>1”是“x>2”的充分不必要条 件,则在下列命题中为真命题的是 (　　)A.p∧(¬q)　　　    B.(¬p)∧(¬q)C.(¬p)∧q　　　    D.p∧q
考点二　含逻辑联结词的命题的真假判断
解析　(1)容易判断当x≤0时,2x≥3x,故命题p为假命题,分别作出函数y=x3,y=1- x2的图象,易知命题q为真命题.根据真值表易判断(¬p)∧q为真命题. 　　(2)由指数函数的性质可知,命题p是真命题,则命题¬p是假命题;显然, “x>1”是“x>2”的必要不充分条件,即命题q是假命题,命题¬q是真命题.所 以命题p∧(¬q)是真命题.
规律总结1.判断含有逻辑联结词的命题的真假的关键及步骤(1)判断含有逻辑联结词的命题的真假的关键是正确理解“或”“且” “非”的含义.(2)判断命题真假的步骤:确定命题的构成形式⇨判断简单命题的真假⇨判断复合命题的真假
2.含有逻辑联结词的命题的真假的等价关系(1)p∨q真⇔p,q至少一个真⇔(¬p)∧(¬q)假.(2)p∨q假⇔p,q均假⇔(¬p)∧(¬q)真.(3)p∧q真⇔p,q均真⇔(¬p)∨(¬q)假.(4)p∧q假⇔p,q至少一个假⇔(¬p)∨(¬q)真.(5)¬p真⇔p假;¬p假⇔p真.
1.已知命题p:∀x>0,ln(x+1)>0;命题q:若a>b,则a2>b2.下列命题为真命题的是 (　　)A.p∧q　　　    B.p∧(¬q)C.(¬p)∧q　　　    D.(¬p)∧(¬q)
解析    当x>0时,x+1>1,因此ln(x+1)>0,即p为真命题;取a=1,b=-2,这时满足 a>b,但显然a2>b2不成立,因此q为假命题.由复合命题的真假性可知选B.
2.“p或q为真命题”是“p且q为真命题”的　　　　     条件.
解析    p或q为真命题⇒/ p且q为真命题,p且q为真命题⇒p或q为真命题.
考点三　由命题的真假确定参数的取值范围 典例2　(1)已知命题“∃x∈R,使2x2+(a-1)x+ ≤0”是假命题,则实数a的取值范围是 (　　)A.(-∞,-1)　　　    B.(-1,3)C.(-3,+∞)　　　    D.(-3,1)
(2)已知a>0,且a≠1,命题p:函数y=lga(x+1)在x∈(0,+∞)内单调递减,命题q:曲 线y=x2+(2a-3)x+1与x轴交于不同的两点.若“p∨q”为假,则a的取值范围是  (　　)A. 　　　    B. ∪ C. 　　　    D. ∪ 
解析　(1)因为命题“∃x∈R,使2x2+(a-1)x+ ≤0”是假命题,所以2x2+(a-1)x+ >0恒成立,所以Δ=(a-1)2-4×2×