数学八年级上册11.2 图形在 坐标中的 平移教案设计

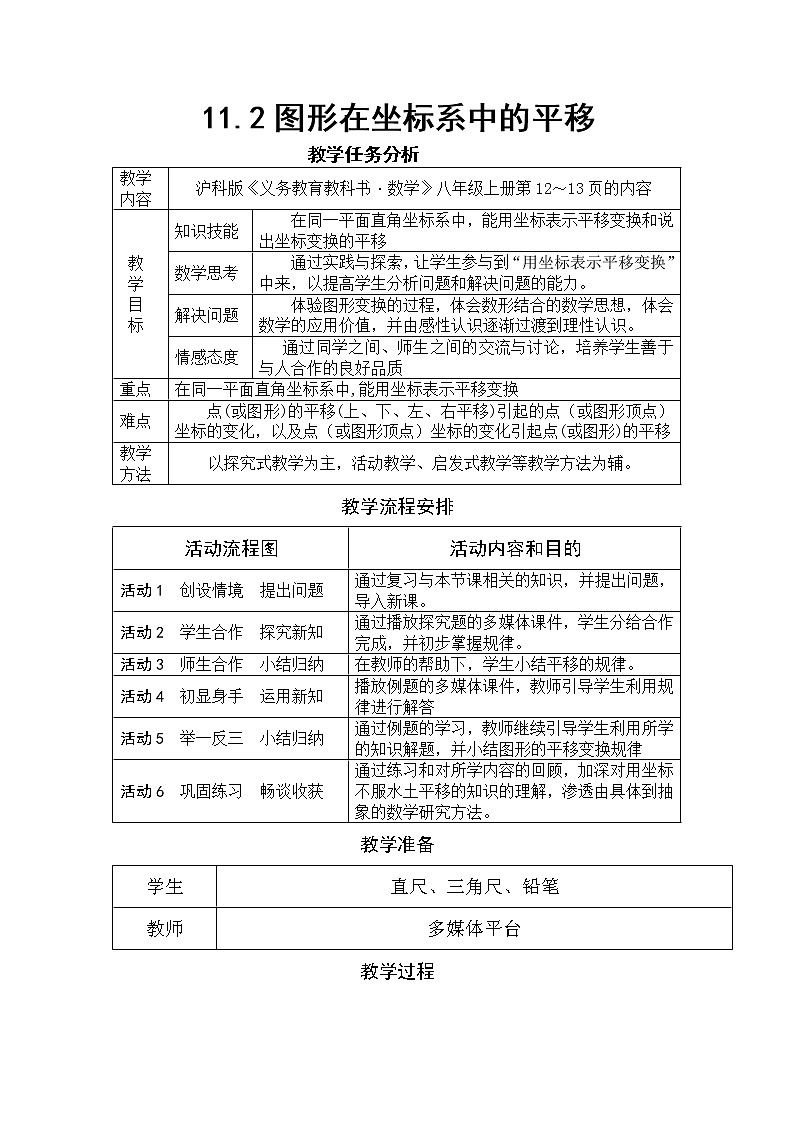
教学

内容

沪科版《义务教育教科书·数学》八年级上册第12～13页的内容

教

学

目

标

知识技能

在同一平面直角坐标系中，能用坐标表示平移变换和说出坐标变换的平移

数学思考

通过实践与探索，让学生参与到“用坐标表示平移变换”中来，以提高学生分析问题和解决问题的能力。

解决问题

体验图形变换的过程，体会数形结合的数学思想，体会数学的应用价值，并由感性认识逐渐过渡到理性认识。

情感态度

通过同学之间、师生之间的交流与讨论，培养学生善于与人合作的良好品质

重点

在同一平面直角坐标系中,能用坐标表示平移变换

难点

点(或图形)的平移(上、下、左、右平移)引起的点（或图形顶点）坐标的变化，以及点（或图形顶点）坐标的变化引起点(或图形)的平移

教学

方法

以探究式教学为主，活动教学、启发式教学等教学方法为辅。

活动流程图

活动内容和目的

活动1  创设情境  提出问题

通过复习与本节课相关的知识，并提出问题，导入新课。

活动2  学生合作  探究新知

通过播放探究题的多媒体课件，学生分给合作完成，并初步掌握规律。

活动3  师生合作  小结归纳

在教师的帮助下，学生小结平移的规律。

活动4  初显身手  运用新知

播放例题的多媒体课件，教师引导学生利用规律进行解答

活动5  举一反三  小结归纳

通过例题的学习，教师继续引导学生利用所学的知识解题，并小结图形的平移变换规律

活动6  巩固练习  畅谈收获

通过练习和对所学内容的回顾，加深对用坐标不服水土平移的知识的理解，渗透由具体到抽象的数学研究方法。

学生

直尺、三角尺、铅笔

教师

多媒体平台

问题与情境

师生行为

设计意图

一、创设情境  提出问题

１、前面我们学习了哪些与坐标有关的知识？

２、请大家组用坐标表示“第三组第二位，第三组第四位”，从而引导学生得出点的位置不同，它们的坐标也不同，因此，把一个点向左或向右平移时，点的坐标会变化吗？有什么规律？

    教师提出问题，学生畅所欲言

学生先独自完成前面的问题，接着教师引导学生进行思考

温故知新，同时也为本节课做准备。

以学生比较熟悉的例子，说明“把一个点平移时，点的坐标会发生变化的”，这样，既让学生比较容易接受，又能激发学生想探求“点的坐标变化规律”。

二、学生合作  探究新知

 根据前面问题，引导学生看教材第51页的“探究”：如图，将点Ａ（-2，-3）向右平移5 个单位长度，得到点B，在图上标出这个点，并写出它的坐标，把点A向上平移4个单位长度呢？把点A向左或向下平移，观察它们坐标的变化，你能从中发现什么规律吗？

再找几个点，对它们进行平移，观察它们的坐标是否按你发现的规律变化。（多媒体课件播放）

学生分组合作完成“探究”前半部分的内容，教师引导学生初步摸索“把一个点向左或向右平移时，点的坐标的变化规律”。然后，运用这个规律，教师要求学生同桌之间互相任意写一个坐标，然后把它向左或向右平移几个单位，看得到什么结果？老师抽查两组，并要求他们简单地说说理由

　　学生既有分工，又有合作，所以能充分地调动他们的积极性。同时，同桌之间互相举例，培养他们养成与人合作的习惯。并且通过教师的抽查，能及时便于教师掌握学生的学习情况，以便于调节教学进度。

三、师生合作  小结归纳

通过探究，我们可以得到：在平面直角坐标系中，将点（ｘ，ｙ）向左（或向右）平移ａ个单位长度，可以得到对应点（ｘ－ａ，ｙ）（或（＿，＿））；将点（ｘ，ｙ）向上（或向下））平移ｂ个单位长度，可以得到对应点（ｘ，ｙ＋ｂ）（或（＿，＿）。

为了更好记忆，可简记为：“上下ｘ不变，左右ｙ不变；右上加，左下减。”

   教师先让学生自己先独立完成填空（当然，确实有困难的，可向同学或老师求助），再与同桌说说这个“归纳”的具体意义。同时，为了更好地记忆，教师应引导学生用自己的语言来小结平规律。

    培养学生的独立解决问题的能力或是与他人合作的能力，同时也培养学生语言叙述和表达能力。

另外，“简记”只是为了学生更好地去记忆，所以教师应加以解释。

四、初显身手  运用新知

前面是探索点的平移规律，若对一个图形进行平移，又该如何呢？我们结合例题解决：

如图，ΔABC三个顶点的坐标分别是A（4，3），B（3，1），C（1，2）。

⑴将ΔABC的横坐标都减去6，纵坐标不变，分别得到点D、E、F，依次连接D、E、F各点，所得ΔDEF与ΔABC的大小、形状和位置有什么关系？

⑵将ΔABC三个顶点的纵坐标都减去5，横坐标不变，分别得到点P、Q、R，依次连接P、Q、R各点，所得ΔPQR与ΔABC的大小、形状和位置有什么关系？（多媒体课件播放）

先让学生自己试着解决问题，若一个人不能解决，可以分组讨论解决，教师让各小组派代表把本小组的解法向全班同学说说。不过，教师解释：对一个图形进行平移，实际上，也是相当于把每一个点进行相应地平移，所以重要地是找出原图形的顶点坐标，然后利用“点的平移规律”，写出新图形的顶点坐标即可

进一步培养学生的独立解决问题的能力或是与他人合作的能力，以及进一步培养学生语言叙述和表达能力，增进师生感情，活跃课堂氛围。

五、举一反三  小结归纳

    由例题引出思考：

    ⑴如果将这个问题中的“横坐标都减去6”“纵坐标都减去5”相应地变为“横坐标加上3”“纵坐标加上2”，分别能得出什么结论？画出得到的图形。

    ⑵如果将三角形ABC三个顶点的横坐标都减去6，同时纵坐标都减去5，能得到什么结论？画出得到的图形。（多媒体课件播放）

从而，归纳得出：

在平面直角坐标系内，如果把一个图形各个点的横坐标都加（或减去）一个正数a，相应的新图形就是把原图形向＿（或向＿）平移＿个单位长度；如果把它各个点的纵坐标都加（或减去）一个正数a，相应的新图形就是把原图形向＿（或向＿）平移＿个单位长度。（多媒体课件播放）

    教师通过引导，要求学生快速回答，并要求学生简单说说理由，然后，用自己的语言来描述把一个图形各个点的横（纵）坐标 都加（或减去）一个正数a的平移规律。

   学生合作完成

    对学生的解题能力、语言叙述和表达能力等等进一步提升。

六、巩固练习  畅谈收获

    1、完成教材第13～14页的练习题

    2、小结：本节课学习了什么内容？你说说看。通过本节课的学习，你有会么收获？说出来，和大家一起分享！

3、作业：教材第14～15页习题11.2的第1、2、3题

学生独立完成，教师对个别辅导

教师应重点关注：学生是否主动发表自己的见解，倾听他人的意见，让每一个学生都有收获。

学生独立完成，教师可以进行适当提醒

巩固新知识，让学生能体验到运用新知识解决问题的乐趣。

同时，鼓励学生充分发表自己的见解和对结果合理性的解释。

通过课后作业，加深对新知识的理解与运用。