广西桂林市2020-2021学年高二下学期期末考试数学（文科）试卷（含答案与解析）

这是一份广西桂林市2020-2021学年高二下学期期末考试数学（文科）试卷（含答案与解析），共13页。试卷主要包含了选择题.，填空题，解答题等内容，欢迎下载使用。
1．已知函数f（x）＝ex，则f'（x）＝（ ）
A．B．exC．lnxD．xex﹣1
2．设复数z＝2﹣i，则z的实部为（ ）
A．﹣1B．2C．﹣2D．i
3．曲线y＝3x2+1在x＝1处的切线的斜率为（ ）
A．6B．5C．4D．3
4．某产品生产厂家的市场部在对4家商场进行调研时，获得该产品的售价x（单位：元）和销售量y（单位：百个）之间的四组数据如表：
用最小二乘法求得销售量y与售价x之间的线性回归方程＝﹣1.4x+17.5，那么表中实数a的值为（ ）
A．4B．4.7C．4.6D．4.5
5．利用反证法证明“若a+b+c＝3，则a，b，c中至少有一个数不小于1”正确的假设为（ ）
A．a，b，c中至多有一个数大于1
B．a，b，c中至多有一个数小于1
C．a，b，c中至少有一个数大于1
D．a，b，c中都小于1
6．（1﹣i）（4+i）＝（ ）
A．3+5iB．3﹣5iC．5+3iD．5﹣3i
7．如果根据性别与是否爱好运动的列联表得到K2≈3.852＞3.841，所以判断性别与运动有关，那么这种判断犯错的可能性不超过（ ）
A．2.5%B．0.5%C．1%D．5%
8．因为对数函数y＝lgax（a＞0，且a≠1）是增函数，而y＝x是对数函数，所以y＝x是增函数，上面的推理错误的是（ ）
A．大前提B．小前提C．推理形式D．以上都是
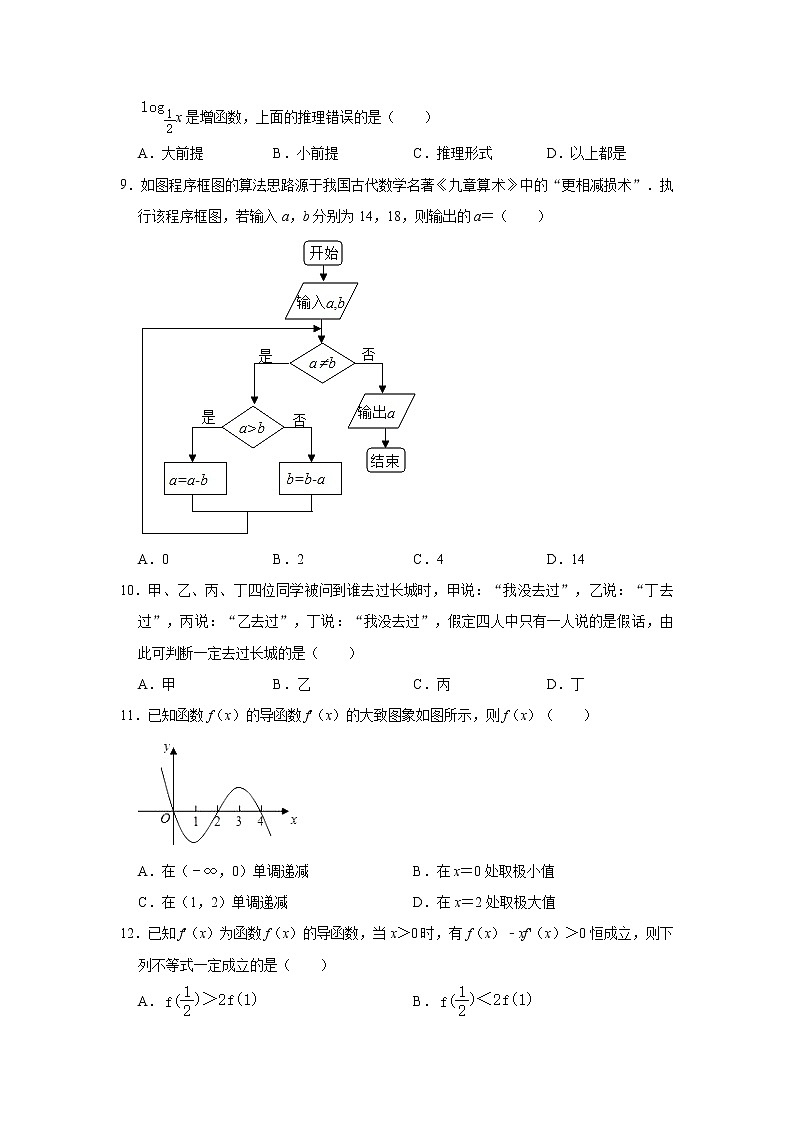
9．如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入a，b分别为14，18，则输出的a＝（ ）
A．0B．2C．4D．14
10．甲、乙、丙、丁四位同学被问到谁去过长城时，甲说：“我没去过”，乙说：“丁去过”，丙说：“乙去过”，丁说：“我没去过”，假定四人中只有一人说的是假话，由此可判断一定去过长城的是（ ）
A．甲B．乙C．丙D．丁
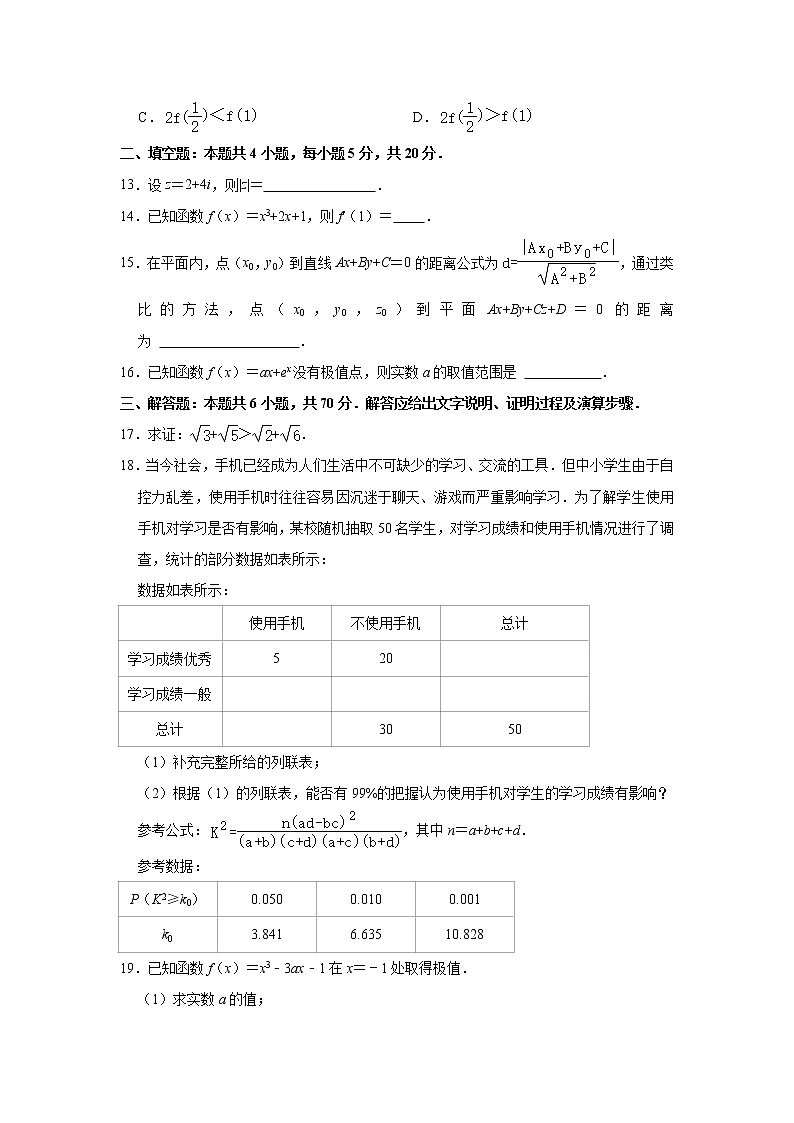
11．已知函数f（x）的导函数f'（x）的大致图象如图所示，则f（x）（ ）
A．在（﹣∞，0）单调递减B．在x＝0处取极小值
C．在（1，2）单调递减D．在x＝2处取极大值
12．已知f'（x）为函数f（x）的导函数，当x＞0时，有f（x）﹣xf'（x）＞0恒成立，则下列不等式一定成立的是（ ）
A．B．
C．D．
二、填空题：本题共4小题，每小题5分，共20分．
13．设z＝2+4i，则|z|＝ ．
14．已知函数f（x）＝x3+2x+1，则f'（1）＝ ．
15．在平面内，点（x0，y0）到直线Ax+By+C＝0的距离公式为，通过类比的方法，点（x0，y0，z0）到平面Ax+By+Cz+D＝0的距离为 ．
16．已知函数f（x）＝ax+ex没有极值点，则实数a的取值范围是 ．
三、解答题：本题共6小题，共70分．解答应给出文字说明、证明过程及演算步骤．
17．求证：+＞+．
18．当今社会，手机已经成为人们生活中不可缺少的学习、交流的工具．但中小学生由于自控力乱差，使用手机时往往容易因沉迷于聊天、游戏而严重影响学习．为了解学生使用手机对学习是否有影响，某校随机抽取50名学生，对学习成绩和使用手机情况进行了调查，统计的部分数据如表所示：
数据如表所示：
（1）补充完整所给的列联表；
（2）根据（1）的列联表，能否有99%的把握认为使用手机对学生的学习成绩有影响？
参考公式：，其中n＝a+b+c+d．
参考数据：
19．已知函数f（x）＝x3﹣3ax﹣1在x＝﹣1处取得极值．
（1）求实数a的值；
（2）当x∈[﹣2，1]时，求函数f（x）的最小值．
20．某种产品的广告费用支出x（万元）与销售额y（万元）之间有如下的对应数据：
（1）作出销售额y关于广告费用支出x的散点图；
（2）建立y关于x的线性回归方程；
（3）试估计广告费用为9万元时，销售额是多少？
参考公式：，．
21．现有一批货物由海上从A地运往B地，已知货船的最大航行速度为35海里/小时，A地至B地之间的航行距离约为500海里，每小时的运输成本由燃料费和其余费用组成，轮船每小时的燃料费用与轮船速度的平方成正比（比例系数为0.6），其余费用为每小时960元．
（1）把全程运输成本y（元）表示为速度x（海里/小时）的函数；
（2）为了使全程运输成本最小，轮船应以多大速度行驶？
22．已知函数f（x）＝aex﹣4x，a∈R．
（1）求函数f（x）的单调区间；
（2）当a＝1时，求证：f（x）+x2+1＞0．
参考答案
一、选择题（共12小题，每小题5分，共60分）.
1．已知函数f（x）＝ex，则f'（x）＝（ ）
A．B．exC．lnxD．xex﹣1
解：∵f（x）＝ex，
∴f′（x）＝ex．
故选：B．
2．设复数z＝2﹣i，则z的实部为（ ）
A．﹣1B．2C．﹣2D．i
解：∵复数z＝2﹣i，
∴z的实部为2．
故选：B．
3．曲线y＝3x2+1在x＝1处的切线的斜率为（ ）
A．6B．5C．4D．3
解：y＝3x2+1的导数为y′＝6x，
由导数的几何意义可得在x＝1处的切线的斜率为k＝6．
故选：A．
4．某产品生产厂家的市场部在对4家商场进行调研时，获得该产品的售价x（单位：元）和销售量y（单位：百个）之间的四组数据如表：
用最小二乘法求得销售量y与售价x之间的线性回归方程＝﹣1.4x+17.5，那么表中实数a的值为（ ）
A．4B．4.7C．4.6D．4.5
解：由表中数据可知，＝×（4+a+5.5+6）＝，＝×（12+11+10+9）＝10.5，
∵线性回归方程＝﹣1.4x+17.5恒过样本中心点（，），
∴10.5＝﹣1.4×+17.5，解得a＝4.5．
故选：D．
5．利用反证法证明“若a+b+c＝3，则a，b，c中至少有一个数不小于1”正确的假设为（ ）
A．a，b，c中至多有一个数大于1
B．a，b，c中至多有一个数小于1
C．a，b，c中至少有一个数大于1
D．a，b，c中都小于1
解：至少一个的否定为至多0个，即都小于1，也就是a，b，c中都小于1．
故选：D．
6．（1﹣i）（4+i）＝（ ）
A．3+5iB．3﹣5iC．5+3iD．5﹣3i
解：（1﹣i）（4+i）＝1×4+1×i﹣i×4﹣i2＝5﹣3i．
故选：D．
7．如果根据性别与是否爱好运动的列联表得到K2≈3.852＞3.841，所以判断性别与运动有关，那么这种判断犯错的可能性不超过（ ）
A．2.5%B．0.5%C．1%D．5%
解：根据性别与是否爱好运动的列联表得到K2≈3.852＞3.841，
所以有95%的把握说明性别与运动有关，
即有1﹣95%＝5%的出错可能性．
故选：D．
8．因为对数函数y＝lgax（a＞0，且a≠1）是增函数，而y＝x是对数函数，所以y＝x是增函数，上面的推理错误的是（ ）
A．大前提B．小前提C．推理形式D．以上都是
解：∵当a＞1时，函数y＝lgax（a＞0且a≠1）是一个增函数，
当0＜a＜1时，此函数是一个减函数
∴y＝lgax（a＞0且a≠1）是增函数这个大前提是错误的，
从而导致结论错．
故选：A．
9．如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入a，b分别为14，18，则输出的a＝（ ）
A．0B．2C．4D．14
解：模拟执行程序框图，可得
a＝14，b＝18
满足条件a≠b，不满足条件a＞b，b＝4
满足条件a≠b，满足条件a＞b，a＝10
满足条件a≠b，满足条件a＞b，a＝6
满足条件a≠b，满足条件a＞b，a＝2
满足条件a≠b，不满足条件a＞b，b＝2
不满足条件a≠b，输出a的值为2．
故选：B．
10．甲、乙、丙、丁四位同学被问到谁去过长城时，甲说：“我没去过”，乙说：“丁去过”，丙说：“乙去过”，丁说：“我没去过”，假定四人中只有一人说的是假话，由此可判断一定去过长城的是（ ）
A．甲B．乙C．丙D．丁
解：若甲去过长城，则甲说假话，乙说假话，丙说假话，丁说真话，不满足条件．
若乙去过长城，则甲说真话，乙说假话，丙说真话，丁说真话，满足条件．
若丙去过长城，则甲说真话，乙说假话，丙说假话，丁说真话，不满足条件．
若丁去过长城，则甲说真话，乙说真话，丙说假话，丁说假话，不满足条件．
故一定去过长城的是乙，
故选：B．
11．已知函数f（x）的导函数f'（x）的大致图象如图所示，则f（x）（ ）
A．在（﹣∞，0）单调递减B．在x＝0处取极小值
C．在（1，2）单调递减D．在x＝2处取极大值
解：由图象可得，当x∈（﹣∞，0）时，f'（x）＞0，f（x）单调递增，
当∈（0，2）时，f'（x）＜0，f（x）单调递减，
当∈（2，4）时，f'（x）＞0，f（x）单调递增，
当∈（4，+∞）时，f'（x）＜0，f（x）单调递减，
故当x＝0，x＝4时，取得极大值，当x＝2时，取得极小值．
故选：C．
12．已知f'（x）为函数f（x）的导函数，当x＞0时，有f（x）﹣xf'（x）＞0恒成立，则下列不等式一定成立的是（ ）
A．B．
C．D．
解：令，x∈（0，+∞），
则，
∵f（x）﹣xf'（x）＞0，
即xf'（x）﹣f（x）＜0，
∴F'（x）＜0，
∴F（x）在x∈（0，+∞）上单调递减，
故，即，
故选：D．
二、填空题：本题共4小题，每小题5分，共20分．
13．设z＝2+4i，则|z|＝ ．
解：因为z＝2+4i，
所以|z|＝＝2．
故答案为：2．
14．已知函数f（x）＝x3+2x+1，则f'（1）＝ 5 ．
解：∵f（x）＝x3+2x+1，∴f′（x）＝3x2+2，
∴f′（1）＝3+2＝5．
故答案为：5．
15．在平面内，点（x0，y0）到直线Ax+By+C＝0的距离公式为，通过类比的方法，点（x0，y0，z0）到平面Ax+By+Cz+D＝0的距离为 d＝ ．
解：∵直线l：Ax+By+C＝0（A，B不同时为0）的一个法向量可以写为＝（A，B），
同时平面内任意一点P（x0，y0）到直线l的距离为；
∴空间中一个平面的方程写为a：Ax+By+Cz+D＝0（A，B，C不同时为0），
则它的一个法向量是（A，B，C），
空间任意一点P（x0，y0，z0）到它的距离d＝，
故答案为：d＝．
16．已知函数f（x）＝ax+ex没有极值点，则实数a的取值范围是 [0，+∞） ．
解：∵f（x）＝ax+ex，
∴f'（x）＝a+ex，
∵函数f（x）＝ax+ex没有极值点，
∴a+ex＝0无解，即a＝﹣ex 无解，
∴a≥0．
故实数a的取值范围为[0，+∞）．
故答案为：[0，+∞）．
三、解答题：本题共6小题，共70分．解答应给出文字说明、证明过程及演算步骤．
17．求证：+＞+．
解：证明：要证明+＞+成立，
只需证明（+）2＞（+）2，…
即3+2+5＞2+2+6，…
从而只需证明2＞2，
即15＞12，这显然成立．…
∴+＞+，证毕． …（16分）
18．当今社会，手机已经成为人们生活中不可缺少的学习、交流的工具．但中小学生由于自控力乱差，使用手机时往往容易因沉迷于聊天、游戏而严重影响学习．为了解学生使用手机对学习是否有影响，某校随机抽取50名学生，对学习成绩和使用手机情况进行了调查，统计的部分数据如表所示：
数据如表所示：
（1）补充完整所给的列联表；
（2）根据（1）的列联表，能否有99%的把握认为使用手机对学生的学习成绩有影响？
参考公式：，其中n＝a+b+c+d．
参考数据：
解：（1）2×2列联表：
（2）∵
∴有99%的把握认为使用手机对学生的学习成绩有影响．
19．已知函数f（x）＝x3﹣3ax﹣1在x＝﹣1处取得极值．
（1）求实数a的值；
（2）当x∈[﹣2，1]时，求函数f（x）的最小值．
解：（1）f′（x）＝3x2﹣3a，
又函数f（x）在x＝﹣1处取得极值，则f′（﹣1）＝3﹣3a＝0；
即a＝1，此时f（x）在（﹣∞，﹣1）上单调递增，在（﹣1，1）上单调递减，在（1，+∞）上单调递增；
所以当a＝1时满足条件；
所以a＝1；
（2）由（1）可知f（x）在[﹣2，﹣1]上单调递增，[﹣1，1]单调递减；
所以 当x∈[﹣2，1]时，函数f（x）的最小值是f（﹣2），f（1）中的较小者；
f（﹣2）＝﹣3，f（1）＝﹣3；
故函数f（x）的最小值为﹣3．
20．某种产品的广告费用支出x（万元）与销售额y（万元）之间有如下的对应数据：
（1）作出销售额y关于广告费用支出x的散点图；
（2）建立y关于x的线性回归方程；
（3）试估计广告费用为9万元时，销售额是多少？
参考公式：，．
解：（1）画出坐标系，把所给的五组点的坐标描到坐标系中，作出散点图如图所示：
（2）设所求线性回归直线方程为，，，，，
，，
因此，所求线性回归方程为．
（3）当x＝9时，y的预报值为y＝6.5×9+17.5＝76（万元），
答：当广告费用为9万元时，销售收入约为76万元．
21．现有一批货物由海上从A地运往B地，已知货船的最大航行速度为35海里/小时，A地至B地之间的航行距离约为500海里，每小时的运输成本由燃料费和其余费用组成，轮船每小时的燃料费用与轮船速度的平方成正比（比例系数为0.6），其余费用为每小时960元．
（1）把全程运输成本y（元）表示为速度x（海里/小时）的函数；
（2）为了使全程运输成本最小，轮船应以多大速度行驶？
解：（1）依题意得，y＝（0＜x≤35）．
所以（0＜x≤35）；
（2）为了使全程运输成本最小，即y最小，
又＝300（），
令f（x）＝，
由对勾函数的单调性可知，f（x）在（0，35]上为减函数，
所以当x＝35时，．
所以为了使全程运输成本最小，轮船应以35海里/小时速度行驶．
22．已知函数f（x）＝aex﹣4x，a∈R．
（1）求函数f（x）的单调区间；
（2）当a＝1时，求证：f（x）+x2+1＞0．
【解答】（1）解：f′（x）＝aex﹣4，
当a≤0时，f′（x）＜0，f（x）在R上单调递减；
当a＞0时，令f′（x）＜0，可得x＜ln，令f′（x）＞0，可得x＞ln，
所以f（x）在（﹣∞，ln）上单调递减，在（ln，+∞）上单调递增．
（2）证明：当a＝1时，f（x）＝ex﹣4x，
令g（x）＝f（x）+x2+1＝ex﹣4x+x2+1，
g′（x）＝ex﹣4+2x，g″（x）＝ex+2＞0恒成立，
所以g′（x）在R上单调递增，g′（0）＝﹣3＜0，g′（1）＝e﹣2＞0，
由零点存在性定理可得存在x0∈（0，1），使得g′（x0）＝0，即﹣4+2x0＝0，
当x∈（﹣∞，x0）时，g′（x）＜0，g（x）单调递减，当x∈（x0，+∞）时，g′（x）＞0，g（x）单调递增，
所以g（x）min＝g（x0）＝﹣4x0+x02+1＝4﹣2x0﹣4x0+x02+1＝x02﹣6x0+5，x0∈（0，1），
由二次函数性质可得g（x）min＞g（1）＝0，
所以g（x）＞0，即f（x）+x2+1＞0，得证．
售价x
4
a
5.5
6
销售量y
12
11
10
9
P（K2≥k）
0.050
0.010
0.001
k
3.841
6.635
10.828
使用手机
不使用手机
总计
学习成绩优秀
5
20
学习成绩一般
总计
30
50
P（K2≥k0）
0.050
0.010
0.001
k0
3.841
6.635
10.828
x
2
4
5
6
8
y
30
40
60
50
70
售价x
4
a
5.5
6
销售量y
12
11
10
9
P（K2≥k）
0.050
0.010
0.001
k
3.841
6.635
10.828
使用手机
不使用手机
总计
学习成绩优秀
5
20
学习成绩一般
总计
30
50
P（K2≥k0）
0.050
0.010
0.001
k0
3.841
6.635
10.828
使用手机
不使用手机
总计
学习成绩优秀
5
20
25
学习成绩一般
15
10
25
总计
20
30
50
x
2
4
5
6
8
y
30
40
60
50
70