广西北海市2020-2021学年高二下学期期末考试数学（文）试题（含答案与解析）

这是一份广西北海市2020-2021学年高二下学期期末考试数学（文）试题（含答案与解析），共15页。试卷主要包含了选择题.，填空题，解答题等内容，欢迎下载使用。
2020-2021学年广西北海市高二（下）期末数学试卷（文科）
一、选择题（共12小题，每小题5分，共60分）.
1．已知集合A＝{x|x2＜2}，B＝{x|x＞0}，则A∩B＝（　　）
A．{x|0＜x＜2} B．
C． D．
2．化简z＝＝（　　）
A．1+i B．1﹣i C．﹣1+i D．﹣1﹣i
3．如表是某厂1～4月份用水量（单位：百吨）的一组数据（　　）
月份x
1
2
3
4
用水量y
4.5
4
3
2.5
用水量y与月份x之间有较好的线性相关关系，其线性回归方程是，则等于（　　）
A．﹣1 B．﹣0.9 C．﹣0.8 D．﹣0.7
4．已知a＝，b＝，c＝，则a，b，c的大小关系是（　　）
A．b＜a＜c B．a＜c＜b C．c＜b＜a D．b＜c＜a
5．用反证法证明命题：“三角形最多有一个内角是钝角”时，假设正确的是（　　）
A．假设三角形最少有两个内角是钝角
B．假设三角形三个内角都不是钝角
C．假设三角形最多有两个内角是钝角
D．假设三角形三个内角都是钝角
6．在极坐标系中，O为极点，曲线ρ2cosθ＝1与射线的交点为A，则|OA|＝（　　）
A．2 B． C． D．
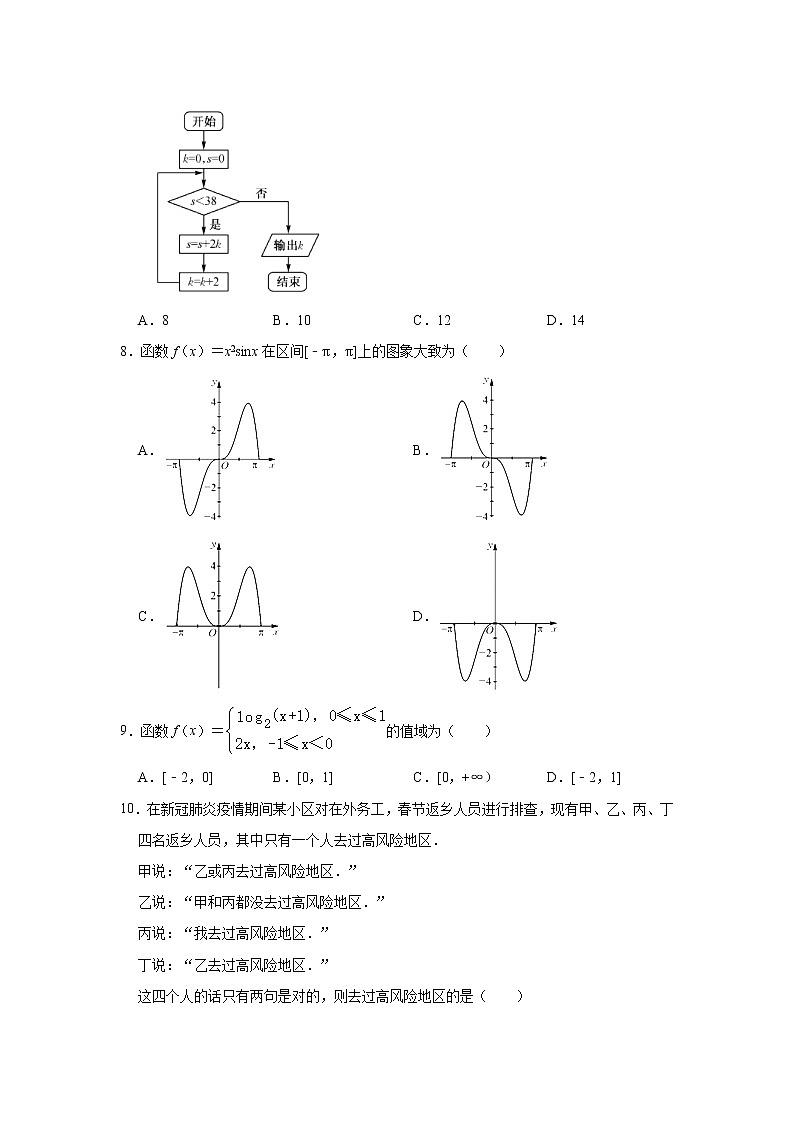
7．若执行如图所示的程序框图，则输出k的值是（　　）

A．8 B．10 C．12 D．14
8．函数f（x）＝x2sinx在区间[﹣π，π]上的图象大致为（　　）
A． B．
C． D．
9．函数f（x）＝的值域为（　　）
A．[﹣2，0] B．[0，1] C．[0，+∞） D．[﹣2，1]
10．在新冠肺炎疫情期间某小区对在外务工，春节返乡人员进行排查，现有甲、乙、丙、丁四名返乡人员，其中只有一个人去过高风险地区．
甲说：“乙或丙去过高风险地区．”
乙说：“甲和丙都没去过高风险地区．”
丙说：“我去过高风险地区．”
丁说：“乙去过高风险地区．”
这四个人的话只有两句是对的，则去过高风险地区的是（　　）
A．甲 B．乙 C．丙 D．丁
11．若函数在（﹣∞，+∞）上单调递增，则实数a的取值范围是（　　）
A．（1，2） B． C． D．（0，1）
12．已知函数，若函数g（x）＝f（x）﹣kx﹣1有且只有三个零点，则实数k的取值范围（　　）
A． B． C．（0，e） D．
二、填空题：本题共4小题，每小题5分，共20分。
13．设复数z满足z（2+i）＝2﹣i，则|z|＝　 　．
14．若函数f（x）＝x2+2bx﹣3a+1为定义在[2a﹣10，3a]上的偶函数，则aa+b＝　 　．
15．设P，Q分别为曲线C：（θ为参数）与直线l：3x﹣4y﹣6＝0上的动点，则|PQ|的最小值为 　 　．
16．某学生在上学路上要经过3个路口，在3个路口遇到红灯的概率依次是，，，假设在各路口是否遇到红灯是相互独立的，则该同学在上学路上至少遇到1个红灯的概率是 　 　．
三、解答题：共70分。解答应写出文字说明、证明过程或演算步骤。
17．已知复数z＝（m+2）（m+3）+（m+2）i（m∈R，i为虚数单位）．
（1）若z是纯虚数，求；
（2）若m＝﹣1，z•i＝a+bi（a，b∈R），求a，b的值．
18．2021年2月12日，辛丑牛年大年初一，由贾玲导演的电影《你好，李焕英》上映，截至到2月21日22点8分，票房攀升至40.25亿，反超同期上映的《唐人街探案3》，迎来了2021春节档最具戏剧性的一幕．正是因为影片中母女间的这份简单、纯粹、诚挚的情感触碰了人们内心柔软的地方，打动了万千观众，才赢得了良好的口碑，不少观众都流下了感动的泪水．影片结束后，某电影院工作人员当日随机抽查了100名观看《你好，李焕英》的观众，询问他们在观看影片的过程中是否“流泪”，得到以下表格：

男性观众
女性观众
合计
流泪
20


没有流泪

5
20
合计



（1）完成表格中的数据，并判断是否有99.9%的把握认为观众在观看影片的过程中流泪与性别有关？
（2）以分层抽样的方式，从流泪与没有流泪的观众中抽取5人，然后从这5人中再随机抽取2人，求这2人都流泪的概率．
附：
P（K2≥k0）
0.100
0.050
0.010
0.001
k0
2.706
3.841
6.635
10.828
，n＝a+b+c+d．
19．在平面直角坐标系xOy中，曲线C：（α是参数）．以O为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为ρcos＝0．
（1）求曲线C的普通方程以及直线l的直角坐标方程；
（2）设P（﹣1，0），直线l与曲线C交于A、两点，求|PA|•|PB|的值．
20．2021年初，S市出现了第一例新冠肺炎本土病例，各大媒体，微信公众号都在报道此事．某微信公众号关于S市疫情的信息发布以后，统计了网友的点击量y与发布时间x的相关数据，如表：
时间x/分钟
5
10
15
20
25
点击量y次
98
193
280
369
460
（1）已知y与x线性相关，利用表格中的数据，求点击量y与发布时间x之间的回归直线方程；
（2）在（1）的条件下，若点击量超过1000次，就达到了宣传效果，那么1小时后，该公众号是否达到了宣传效果？
参考公式：，．
21．在数列{an}中，an+1＝3an+2（n＞0且n∈N*），a1＝2．
（1）求a2，a3，a4；
（2）归纳猜想数列{an}的通项公式，并证明；
（3）求数列{an}的前n项和Sn．
22．已知定义在R上的函数f（x）＝是奇函数
（1）求a，b的值；
（2）若对任意的t∈R，不等式f（t﹣2t2）+f（﹣k）＞0恒成立，求k的取值范围．


参考答案
一、选择题（共12小题，每小题5分，共60分）.
1．已知集合A＝{x|x2＜2}，B＝{x|x＞0}，则A∩B＝（　　）
A．{x|0＜x＜2} B．
C． D．
解：∵，B＝{x|x＞0}，
∴A∩B＝．
故选：D．
2．化简z＝＝（　　）
A．1+i B．1﹣i C．﹣1+i D．﹣1﹣i
解：z＝＝．
故选：D．
3．如表是某厂1～4月份用水量（单位：百吨）的一组数据（　　）
月份x
1
2
3
4
用水量y
4.5
4
3
2.5
用水量y与月份x之间有较好的线性相关关系，其线性回归方程是，则等于（　　）
A．﹣1 B．﹣0.9 C．﹣0.8 D．﹣0.7
解：由于回归直线必经过点，而＝＝2.5，＝＝3.5，
线性回归方程是，∴3.5＝×2.5+5.25，
∴＝﹣0.7．
故选：D．
4．已知a＝，b＝，c＝，则a，b，c的大小关系是（　　）
A．b＜a＜c B．a＜c＜b C．c＜b＜a D．b＜c＜a
解：由已知可得：a＞＝1，b＜＝0，c∈（0，1），
∴b＜c＜a．
故选：D．
5．用反证法证明命题：“三角形最多有一个内角是钝角”时，假设正确的是（　　）
A．假设三角形最少有两个内角是钝角
B．假设三角形三个内角都不是钝角
C．假设三角形最多有两个内角是钝角
D．假设三角形三个内角都是钝角
解：“三角形最多有一个内角是钝角”包括：
“三角形没有一个内角是钝角”和“三角形有一个内角是钝角”两种情况，
它的反面是“三角形有两个内角是钝角”和“三角形有三个内角是钝角”，
即“三角形最少有两个内角是钝角”，
故选：A．
6．在极坐标系中，O为极点，曲线ρ2cosθ＝1与射线的交点为A，则|OA|＝（　　）
A．2 B． C． D．
解：将代入ρ2cosθ＝1得ρ2＝2，
则．
故选：B．
7．若执行如图所示的程序框图，则输出k的值是（　　）

A．8 B．10 C．12 D．14
解：模拟程序的运行，可得
k＝0，s＝0
满足条件s＜38，执行循环体，s＝0，k＝2
满足条件s＜38，执行循环体，s＝4，k＝4
满足条件s＜38，执行循环体，s＝12，k＝6
满足条件s＜38，执行循环体，s＝24，k＝8
满足条件s＜38，执行循环体，s＝40，k＝10
此时，不满足条件s＜38，退出循环，输出k的值为10．
故选：B．
8．函数f（x）＝x2sinx在区间[﹣π，π]上的图象大致为（　　）
A． B．
C． D．
解：根据题意，f（x）＝x2sinx，x∈[﹣π，π]，
f（）＝＞0，排除B、D，
而f（﹣）＝﹣＜0，排除C，
故选：A．
9．函数f（x）＝的值域为（　　）
A．[﹣2，0] B．[0，1] C．[0，+∞） D．[﹣2，1]
解：∵函数f（x）＝，
当0≤x≤1时，1≤x+1≤2，所以，0≤log2（x+1）≤1；
当﹣1≤x＜0时，﹣2≤2x＜0．
综上可得，函数的值域为[﹣2，1]，
故选：D．
10．在新冠肺炎疫情期间某小区对在外务工，春节返乡人员进行排查，现有甲、乙、丙、丁四名返乡人员，其中只有一个人去过高风险地区．
甲说：“乙或丙去过高风险地区．”
乙说：“甲和丙都没去过高风险地区．”
丙说：“我去过高风险地区．”
丁说：“乙去过高风险地区．”
这四个人的话只有两句是对的，则去过高风险地区的是（　　）
A．甲 B．乙 C．丙 D．丁
解：假设甲去过高风险地区，则四人说的都是假话，与题意不符；
假设乙去过高风险地区，则甲、乙、丁说的都是真话，与题意不符；
假设丙去过高风险地区，则甲、丙说的是真话，乙、丁说的是假话，符合题意；
假设丁去过高风险地区，则甲、丙、丁说的都是假话，与题意不符．
故选：C．
11．若函数在（﹣∞，+∞）上单调递增，则实数a的取值范围是（　　）
A．（1，2） B． C． D．（0，1）
解：∵函数在（﹣∞，+∞）上单调递增，则有 ，解得 ≤a＜2，
故选：C．
12．已知函数，若函数g（x）＝f（x）﹣kx﹣1有且只有三个零点，则实数k的取值范围（　　）
A． B． C．（0，e） D．
【解答】解：f（x）＝，如图所示：函数g（x）＝f（x）﹣kx﹣1有且只有三个零点得f（x）＝kx+1，相当于两个函数有3个交点，令h（x）＝kx+1，恒过（0，1），h（x）中k＞0与f（x）在x＜0一定有一个交点，与x＞0的f（x）相切时是两个交点，f'（x）＝，设切点（x，lnx）则又过（0，1）∴＝∴x＝e2，即k＝时与右边相切，这时是两个交点，所以3个交点时是：0．
故选：A．
二、填空题：本题共4小题，每小题5分，共20分。
13．设复数z满足z（2+i）＝2﹣i，则|z|＝　1　．
解：因为z（2+i）＝2﹣i，
所以z（2+i）（2﹣i）＝（2﹣i）（2﹣i），
所以5z＝3﹣4i，即，
所以|z|＝1，
故答案为：1．
14．若函数f（x）＝x2+2bx﹣3a+1为定义在[2a﹣10，3a]上的偶函数，则aa+b＝　4　．
解：根据题意，函数f（x）的定义域为[2a﹣10，3a]，则2a﹣10+3a＝0，解得a＝2，
所以f（x）＝x2+2bx﹣5，是二次函数，其对称轴x＝﹣b，
必有x＝﹣b＝0，即b＝0，
则aa+b＝22+0＝4，
故答案为：4．
15．设P，Q分别为曲线C：（θ为参数）与直线l：3x﹣4y﹣6＝0上的动点，则|PQ|的最小值为 　1　．
解：曲线C：（θ为参数）转换为直角坐标方程为（x﹣1）2+（y﹣3）2＝4，
所以圆心（1，3）到直线3x﹣4y﹣6＝0的距离d＝，
所以|PQ|min＝3﹣2＝1．
故答案为：1．
16．某学生在上学路上要经过3个路口，在3个路口遇到红灯的概率依次是，，，假设在各路口是否遇到红灯是相互独立的，则该同学在上学路上至少遇到1个红灯的概率是 　　．
解：记这名学生在第一个路口遇到红灯为事件A，
在第二个路口遇到红灯为事件B，
在第三个路口遇到红灯为事件C．
这名学生在三个路口都没遇到红灯的概率为，
所以这名同学在上学路上至少遇到1个红灯的概率．
故答案为：．
三、解答题：共70分。解答应写出文字说明、证明过程或演算步骤。
17．已知复数z＝（m+2）（m+3）+（m+2）i（m∈R，i为虚数单位）．
（1）若z是纯虚数，求；
（2）若m＝﹣1，z•i＝a+bi（a，b∈R），求a，b的值．
解：（1）因为z＝（m+2）（m+3）+（m+2）i是纯虚数，
所以解得m＝﹣3，
所以z＝﹣i，所以．
（2）由m＝﹣1，得z＝2+i，代入z⋅i＝a+bi中，
得（2+i）i＝﹣1+2i＝a+bi，所以a＝﹣1，b＝2．
18．2021年2月12日，辛丑牛年大年初一，由贾玲导演的电影《你好，李焕英》上映，截至到2月21日22点8分，票房攀升至40.25亿，反超同期上映的《唐人街探案3》，迎来了2021春节档最具戏剧性的一幕．正是因为影片中母女间的这份简单、纯粹、诚挚的情感触碰了人们内心柔软的地方，打动了万千观众，才赢得了良好的口碑，不少观众都流下了感动的泪水．影片结束后，某电影院工作人员当日随机抽查了100名观看《你好，李焕英》的观众，询问他们在观看影片的过程中是否“流泪”，得到以下表格：

男性观众
女性观众
合计
流泪
20


没有流泪

5
20
合计



（1）完成表格中的数据，并判断是否有99.9%的把握认为观众在观看影片的过程中流泪与性别有关？
（2）以分层抽样的方式，从流泪与没有流泪的观众中抽取5人，然后从这5人中再随机抽取2人，求这2人都流泪的概率．
附：
P（K2≥k0）
0.100
0.050
0.010
0.001
k0
2.706
3.841
6.635
10.828
，n＝a+b+c+d．
解：（1）

男性观众
女性观众
合计
流泪
20
60
80
没有流泪
15
5
20
合计
35
65
100

所以有99.9%的把握认为观众在观看影片的过程中流泪与性别有关．
（2）以分层抽样的方式，从流泪与没有流泪的观众中抽取5人，则
流泪的观众抽到人，记为a，b，c，d，没有流泪的观众抽到人，记为A
从这5人中抽2人有10种情况，分别是ab，ac，ad，aA，bc，bd，bA，cd，cA，dA．
其中这2人都流泪有6种情况，分别是ab，ac，ad，bc，bd，cd．
所以所求概率．
19．在平面直角坐标系xOy中，曲线C：（α是参数）．以O为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为ρcos＝0．
（1）求曲线C的普通方程以及直线l的直角坐标方程；
（2）设P（﹣1，0），直线l与曲线C交于A、两点，求|PA|•|PB|的值．
解：（1）曲线C：（α是参数），转换为直角坐标方程为，
直线l的极坐标方程为ρcos＝0，根据，转换为直角坐标方程为x﹣y+1＝0．
（2）设P（﹣1，0），直线的参数方程（t为参数），
把直线的参数方程，代入得到：；
所以|PA||PB|＝．
20．2021年初，S市出现了第一例新冠肺炎本土病例，各大媒体，微信公众号都在报道此事．某微信公众号关于S市疫情的信息发布以后，统计了网友的点击量y与发布时间x的相关数据，如表：
时间x/分钟
5
10
15
20
25
点击量y次
98
193
280
369
460
（1）已知y与x线性相关，利用表格中的数据，求点击量y与发布时间x之间的回归直线方程；
（2）在（1）的条件下，若点击量超过1000次，就达到了宣传效果，那么1小时后，该公众号是否达到了宣传效果？
参考公式：，．
解：（1），
，
，
，
所以，
，
所以点击量y与发布时间x之间的回归直线方程为．
（2）令x＝60，得
所以1小时后，该公众号信息的点击量约为1090次，达到了宣传效果．
21．在数列{an}中，an+1＝3an+2（n＞0且n∈N*），a1＝2．
（1）求a2，a3，a4；
（2）归纳猜想数列{an}的通项公式，并证明；
（3）求数列{an}的前n项和Sn．
解：（1）令n＝1，得a2＝3a1+2＝8；令n＝2，得a3＝3a2+2＝26；令n＝3，得a4＝3a3+2＝80，
（2）由于，，，，…，
故猜想．证明如下：
由an+1＝3an+2，得an+1+1＝3（an+1），所以，
又a1+1＝3，所以数列{an+1}是以3为首项，3为公比的等比数列．
所以，．
（2）．
22．已知定义在R上的函数f（x）＝是奇函数
（1）求a，b的值；
（2）若对任意的t∈R，不等式f（t﹣2t2）+f（﹣k）＞0恒成立，求k的取值范围．
解：（1）∵f（x）是奇函数，∴f（0）＝0，∴b＝1，
∵f（﹣1）＝﹣f（1），∴＝﹣，∴a＝1；
（2）由（1）知f（x）＝﹣1+，
∴f′（x）＝＜0
∴f（x）在（﹣∞，+∞）上为减函数，
所以（t﹣2t2）+f（﹣k）＞0等价于t﹣2t2＜k，
∴k＞t﹣2t2＝﹣2+对任意t∈R恒成立，
∴k＞．