高考数学(理数)一轮课后刷题练习：第2章　函数、导数及其应用2.9(教师版)

这是一份高考数学(理数)一轮课后刷题练习：第2章　函数、导数及其应用2.9(教师版)，共10页。
一、选择题
1．在一次数学实验中，运用计算器采集到如下一组数据：
则y关于x的函数关系与下列函数最接近的(其中a，b为待定系数)是( )
A．y＝a＋bx B．y＝a＋bx
C．y＝ax2＋b D．y＝a＋eq \f(b,x)
答案 B
解析 由x＝0时，y＝1，排除D；由f(－1.0)≠f(1.0)，排除C；由函数值增长速度不同，排除A.故选B.
2．某工厂6年来生产某种产品的情况是：前三年年产量的增长速度越来越快，后三年年产量保持不变，则该厂6年来这种产品的总产量C与时间t(年)的函数关系可用图象表示的是( )
答案 A
解析 由于开始的三年产量的增长速度越来越快，故总产量迅速增长，图中符合这个规律的只有选项A；后三年产量保持不变，总产量直线上升，故选A.
3．某杂志每本原定价2元，可发行5万本，若每本提价0.20元，则发行量减少4000本，为使销售总收入不低于9万元，需要确定杂志的最高定价是( )
A．2.4元 B．3元 C．2.8元 D．3.2元
答案 B
解析 设每本定价x元(x≥2)，销售总收入是y元，则y＝eq \b\lc\[\rc\](\a\vs4\al\c1(5×104－\f(x－2,0.2)×4×103))·x＝104·x(9－2x)≥9×104.
∴2x2－9x＋9≤0⇒eq \f(3,2)≤x≤3，故选B.
4．某公司租地建仓库，每月土地费用与仓库到车站距离成反比，而每月货物的运输费用与仓库到车站距离成正比．如果在距离车站10 km处建仓库，则土地费用和运输费用分别为2万元和8万元，那么要使两项费用之和最小，仓库应建在离车站( )
A．5 km处 B．4 km处 C．3 km处 D．2 km处
答案 A
解析 设仓库与车站距离为x，土地费用为y1，运输费用为y2，于是y1＝eq \f(k1,x)，y2＝k2x，∴eq \b\lc\{\rc\ (\a\vs4\al\c1(2＝\f(k1,10)，,8＝10k2，))解得k1＝20，k2＝eq \f(4,5).
设总费用为y，则y＝eq \f(20,x)＋eq \f(4x,5)≥2eq \r(\f(20,x)·\f(4x,5))＝8.
当且仅当eq \f(20,x)＝eq \f(4x,5)，即x＝5时取等号．故选A.
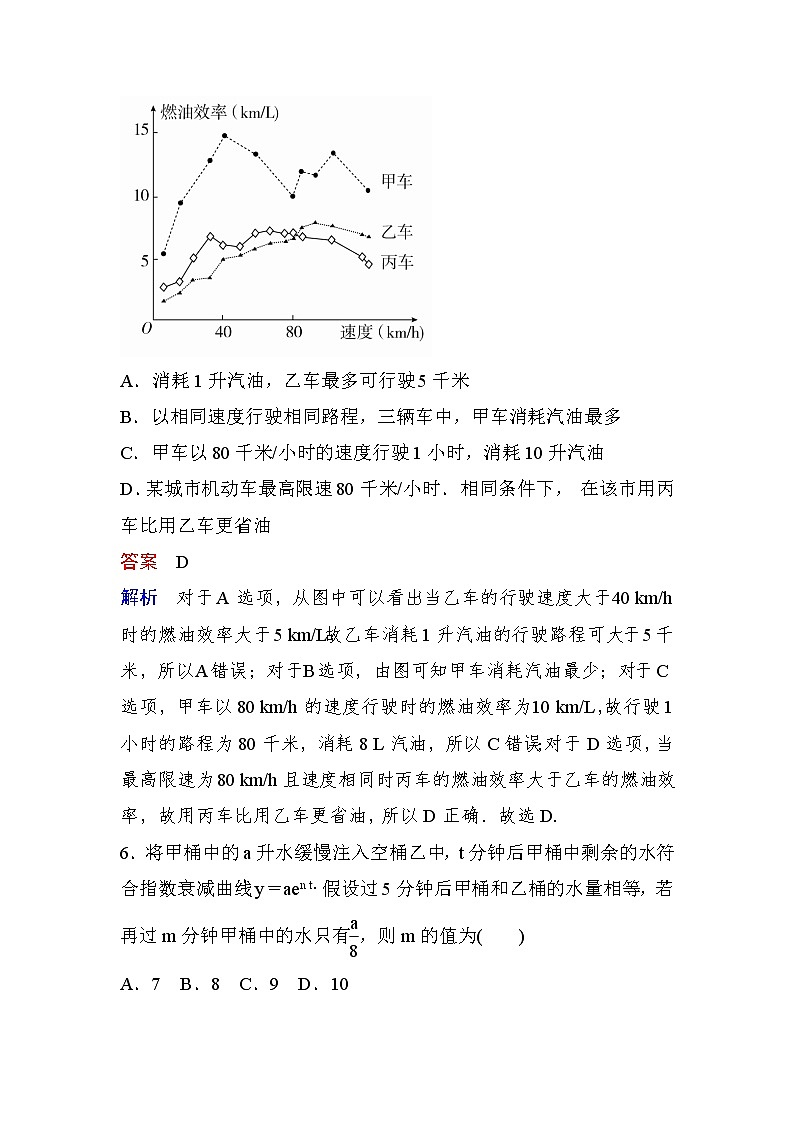
5．汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程，下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况．下列叙述中正确的是( )
A．消耗1升汽油，乙车最多可行驶5千米
B．以相同速度行驶相同路程，三辆车中，甲车消耗汽油最多
C．甲车以80千米/小时的速度行驶1小时，消耗10升汽油
D．某城市机动车最高限速80千米/小时．相同条件下， 在该市用丙车比用乙车更省油
答案 D
解析 对于A选项，从图中可以看出当乙车的行驶速度大于40 km/h时的燃油效率大于5 km/L，故乙车消耗1升汽油的行驶路程可大于5千米，所以A错误；对于B选项，由图可知甲车消耗汽油最少；对于C选项，甲车以80 km/h的速度行驶时的燃油效率为10 km/L，故行驶1小时的路程为80千米，消耗8 L汽油，所以C错误；对于D选项，当最高限速为80 km/h且速度相同时丙车的燃油效率大于乙车的燃油效率，故用丙车比用乙车更省油，所以D正确．故选D.
6．将甲桶中的a升水缓慢注入空桶乙中，t分钟后甲桶中剩余的水符合指数衰减曲线y＝aen t．假设过5分钟后甲桶和乙桶的水量相等，若再过m分钟甲桶中的水只有eq \f(a,8)，则m的值为( )
A．7 B．8 C．9 D．10
答案 D
解析 根据题意知eq \f(1,2)＝e5n，令eq \f(1,8)a＝aen t，即eq \f(1,8)＝en t，
因为eq \f(1,2)＝e5n，故eq \f(1,8)＝e15n，比较知t＝15，m＝15－5＝10.故选D.
7．国家规定某行业征税如下：年收入在280万元及以下的税率为p%，超过280万元的部分按(p＋2)%征税，有一公司的实际缴税比例为(p＋0.25)%，则该公司的年收入是( )
A．560万元 B．420万元 C．350万元 D．320万元
答案 D
解析 设该公司的年收入为x万元，纳税额为y万元，则由题意得
y＝eq \b\lc\{\rc\ (\a\vs4\al\c1(x×p%，x≤280，,280×p%＋x－280×p＋2%，x>280，))
依题有eq \f(280×p%＋x－280×p＋2%,x)＝(p＋0.25)%，解得x＝320.故选D.
8．假设你有一笔资金用于投资，现有三种投资方案供你选择，这三种方案每天的回报如图所示．
横轴为投资时间，纵轴为每天的回报，根据以上信息，若使回报最多，下列说法错误的是( )
A．投资3天以内(含3天)，采用方案一
B．投资4天，不采用方案三
C．投资6天，采用方案一
D．投资12天，采用方案二
答案 D
解析 由图可知，投资3天以内(含3天)，方案一的回报最高，A正确；投资4天，方案一的回报约为40×4＝160(元)，方案二的回报约为10＋20＋30＋40＝100(元)，都高于方案三的回报，B正确；投资6天，方案一的回报约为40×6＝240(元)，方案二的回报约为10＋20＋30＋40＋50＋60＝210(元)，都高于方案三的回报，C正确；投资12天，明显方案三的回报最高，所以此时采用方案三，D错误．故选D.
9．当生物死亡后，其体内原有的碳14的含量大约每经过5730年衰减为原来的一半，这个时间称为“半衰期”．当死亡生物体内的碳14含量不足死亡前的千分之一时，用一般的放射性探测器就测不到了．若某死亡生物体内的碳14用一般的放射性探测器探测不到，则它经过的“半衰期”个数至少是( )
A．8 B．9 C．10 D．11
答案 C
解析 设死亡生物体内原有的碳14含量为1，则经过n(n∈N*)个“半衰期”后的含量为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))n，由eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))n0.1)) (2)0.6
解析 (1)设y＝kt，由图象知y＝kt过点(0.1,1)，
则1＝k×0.1，k＝10，∴y＝10t(0≤t≤0.1)．
由y＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,16)))t－a过点(0.1,1)，得1＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,16)))0.1－a，解得a＝0.1，∴y＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,16)))t－0.1(t>0.1)．
(2)由eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,16)))t－0.1≤0.25＝eq \f(1,4)，得t≥0.6.
故至少需经过0.6小时学生才能回到教室．
三、解答题
15．已知某商品的进货单价为1元/件，商户甲往年以单价2元/件销售该商品时，年销量为1万件，今年拟下调销售单价以提高销量增加收益．据估算，若今年的实际销售单价为x元/件(1≤x≤2)，则新增的年销量P＝4(2－x)2(万件)．
(1)写出今年商户甲的收益f(x)(单位：万元)与x的函数关系式；
(2)商户甲今年采取降低单价提高销量的营销策略，是否能获得比往年更大的收益(即比往年收益更多)？请说明理由．
解 (1)由题意可得：f(x)＝[1＋4(2－x)2](x－1)，1≤x≤2.
(2)甲往年以单价2元/件销售该商品时，年销量为1万件，可得收益为1万元．
f′(x)＝8(x－2)(x－1)＋1＋4(2－x)2＝12x2－40x＋33＝(2x－3)(6x－11)，
可得当x∈eq \b\lc\[\rc\)(\a\vs4\al\c1(1，\f(3,2)))时，函数f(x)单调递增；
当x∈eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3,2)，\f(11,6)))时，函数f(x)单调递减；
当x∈eq \b\lc\(\rc\](\a\vs4\al\c1(\f(11,6)，2))时，函数f(x)单调递增．
∴x＝eq \f(3,2)时，函数f(x)取得极大值，feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3,2)))＝1；又f(2)＝1.
∴当x＝eq \f(3,2)或x＝2时，函数f(x)取得最大值1(万元)．
因此商户甲今年采取降低单价提高销量的营销策略，不能获得比往年更大的收益．
16．已知甲、乙两个工厂在今年的1月份的利润都是6万元，且乙厂在2月份的利润是8万元．若甲、乙两个工厂的利润(万元)与月份x之间的函数关系式分别符合下列函数模型：f(x)＝a1x2－4x＋6，g(x)＝a2·3x＋b2(a1，a2，b2∈R)．
(1)求函数f(x)与g(x)的解析式；
(2)求甲、乙两个工厂今年5月份的利润；
(3)在同一直角坐标系下画出函数f(x)与g(x)的草图，并根据草图比较今年1～10月份甲、乙两个工厂的利润的大小情况．
解 (1)依题意：由f(1)＝6，解得a1＝4，
所以f(x)＝4x2－4x＋6.
由eq \b\lc\{\rc\ (\a\vs4\al\c1(g1＝6，,g2＝8，))得eq \b\lc\{\rc\ (\a\vs4\al\c1(3a2＋b2＝6，,9a2＋b2＝8，))
解得a2＝eq \f(1,3)，b2＝5，
所以g(x)＝eq \f(1,3)×3x＋5＝3x－1＋5.
(2)由(1)知甲厂在今年5月份的利润为f(5)＝86万元，乙厂在今年5月份的利润为g(5)＝86万元，故有f(5)＝g(5)，即甲、乙两个工厂今年5月份的利润相等．
(3)作函数图象如下：
从图中可以看出今年1～10月份甲、乙两个工厂的利润：
当x＝1或x＝5时，有f(x)＝g(x)；
当x＝2,3,4时，有f(x)>g(x)；
当x＝6,7,8,9,10时，有f(x)