高考数学(理数)一轮课后刷题练习：第7章　立体几何7.1(教师版)

这是一份高考数学(理数)一轮课后刷题练习：第7章　立体几何7.1(教师版)，共15页。
一、选择题
1．一个几何体的三视图如图所示，则该几何体的直观图可以是( )
答案 D
解析 由俯视图是圆环可排除A，B，C，进一步将已知三视图还原为几何体，故选D.
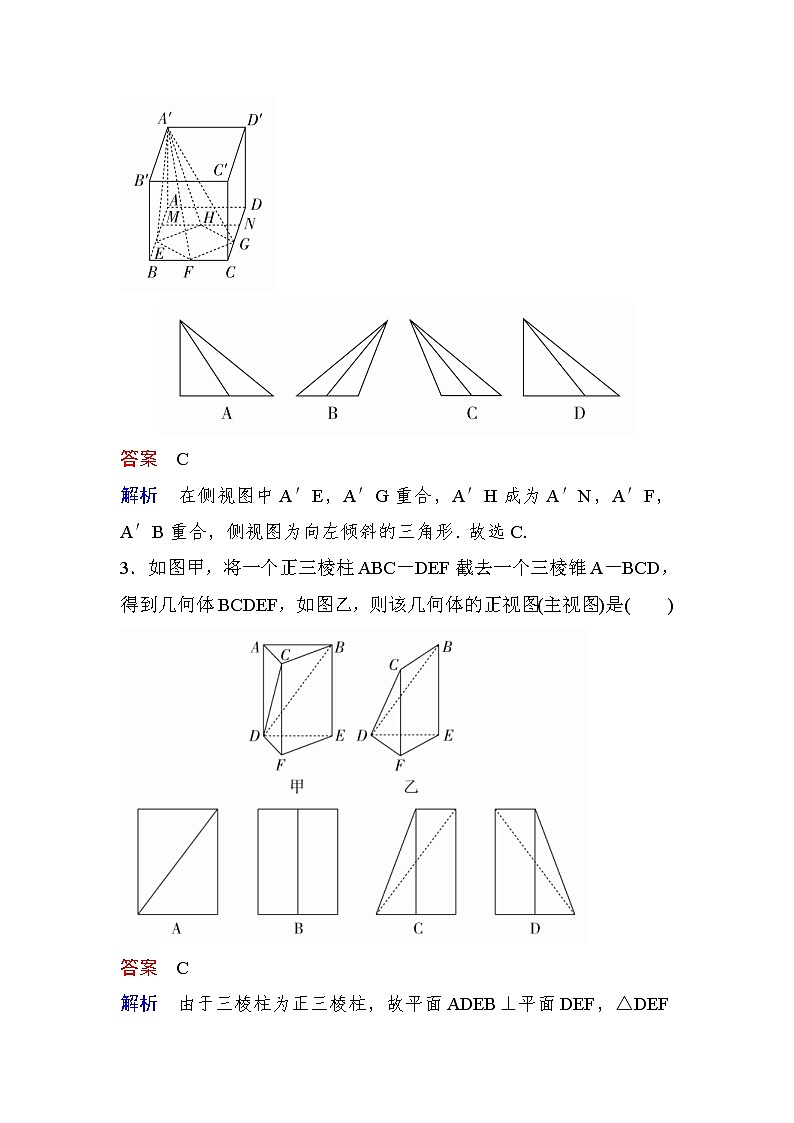
2．如图所示，在正方体ABCD－A′B′C′D′中，M，E是AB的三等分点，G，N是CD的三等分点，F，H分别是BC，MN的中点，则四棱锥A′－EFGH的侧视图为 ( )
答案 C
解析 在侧视图中A′E，A′G重合，A′H成为A′N，A′F，A′B重合，侧视图为向左倾斜的三角形．故选C.
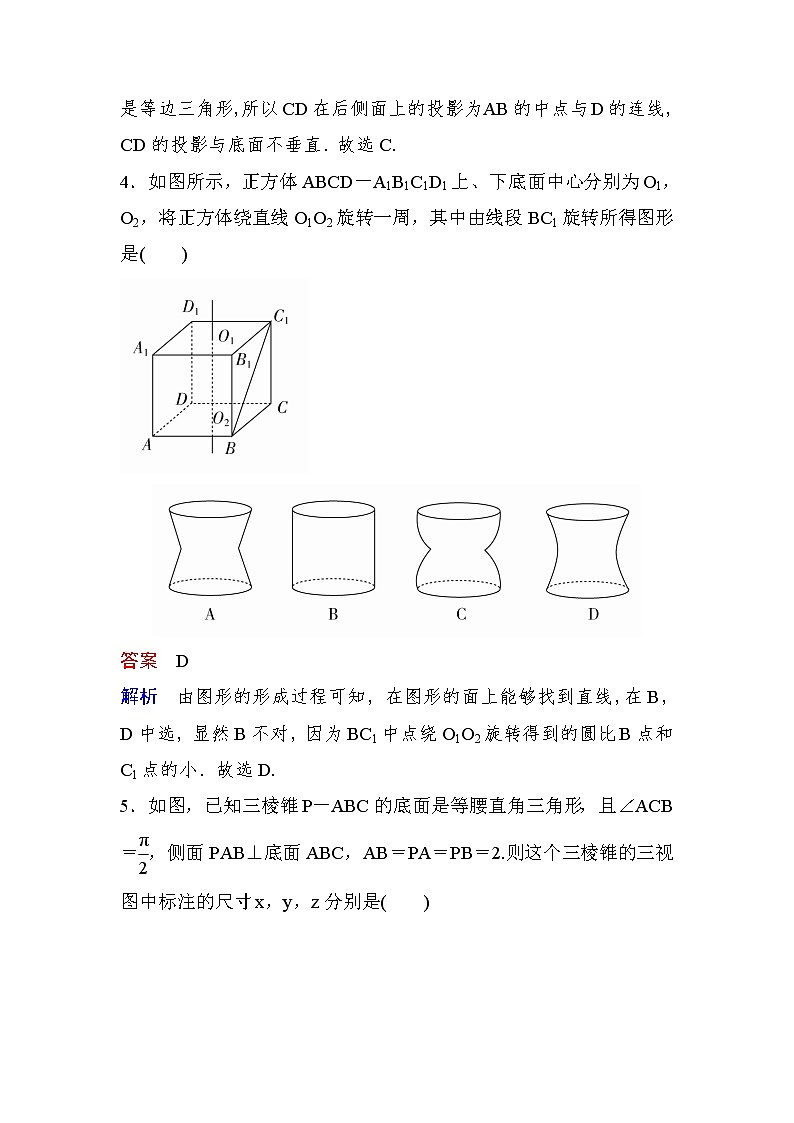
3．如图甲，将一个正三棱柱ABC－DEF截去一个三棱锥A－BCD，得到几何体BCDEF，如图乙，则该几何体的正视图(主视图)是( )
答案 C
解析 由于三棱柱为正三棱柱，故平面ADEB⊥平面DEF，△DEF是等边三角形，所以CD在后侧面上的投影为AB的中点与D的连线，CD的投影与底面不垂直．故选C.
4．如图所示，正方体ABCD－A1B1C1D1上、下底面中心分别为O1，O2，将正方体绕直线O1O2旋转一周，其中由线段BC1旋转所得图形是( )
答案 D
解析 由图形的形成过程可知，在图形的面上能够找到直线，在B，D中选，显然B不对，因为BC1中点绕O1O2旋转得到的圆比B点和C1点的小．故选D.
5．如图，已知三棱锥P－ABC的底面是等腰直角三角形，且∠ACB＝eq \f(π,2)，侧面PAB⊥底面ABC，AB＝PA＝PB＝2.则这个三棱锥的三视图中标注的尺寸x，y，z分别是( )
A.eq \r(3)，1，eq \r(2) B.eq \r(3)，1,1
C．2,1，eq \r(2) D．2,1,1
答案 B
解析 ∵三棱锥P－ABC的底面是等腰直角三角形，且∠ACB＝eq \f(π,2)，侧面PAB⊥底面ABC，AB＝PA＝PB＝2；
∴x是等边△PAB边AB上的高，x＝2sin60°＝eq \r(3)，
y是边AB的一半，y＝eq \f(1,2)AB＝1，z是等腰直角△ABC斜边AB上的中线，z＝eq \f(1,2)AB＝1；
∴x，y，z分别是eq \r(3)，1,1.故选B.
6．一个四面体的顶点在空间直角坐标系Oxyz中的坐标分别是(0,0,0)，(1,0,1)，(0,1,1)，eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)，1，0))，绘制该四面体三视图时，按照如图所示的方向画正视图，则得到侧(左)视图可以为( )
答案 B
解析 满足条件的四面体如下图，
依题意投影到yOz平面为正投影，所以侧(左)视方向如图所示，所以得到侧(左)视图效果如上图．故选B.
7．一只蚂蚁从正方体ABCD－A1B1C1D1的顶点A出发，经正方体的表面，按最短路线爬行到顶点C1的位置，则下列图形中可以表示正方体及蚂蚁最短爬行路线的正视图的是( )
A．①② B．①③
C．③④ D．②④
答案 D
解析 由点A经正方体的表面，按最短路线爬行到达顶点C1的位置，共有6种路线(对应6种不同的展开方式)，若把平面ABB1A1和平面BCC1B1展到同一个平面内，连接AC1，则AC1是最短路线，且AC1会经过BB1的中点，此时对应的正视图为②；若把平面ABCD和平面CDD1C1展到同一个平面内，连接AC1，则AC1是最短路线，且AC1会经过CD的中点，此时对应的正视图为④.而其他几种展开方式对应的正视图在题中没有出现．故选D.
8．某几何体的正视图和侧视图如图1，它的俯视图的直观图是矩形O1A1B1C1，如图2，其中O1A1＝6，O1C1＝2，则该几何体的侧面积为( )
A．48 B．64
C．96 D．128
答案 C
解析 由题图2及斜二测画法可知原俯视图为如图所示的平行四边形OABC，设CB与y轴的交点为D，则易知CD＝2，OD＝2×2eq \r(2)＝4eq \r(2)，∴CO＝eq \r(CD2＋OD2)＝6＝OA，∴俯视图是以6为边长的菱形，由三视图知几何体为一个直四棱柱，其高为4，所以该几何体的侧面积为4×6×4＝96.故选C.
9．早在公元前三百多年我国已经运用“以度审容”的科学方法，其中商鞅铜方升是公元前344年商鞅督造的一种标准量器，其三视图如图所示(单位：寸)，若π取3，其体积为12.6(立方寸)，则图中的x为( )
A．1.2 B．1.6
C．1.8 D．2.4
答案 B
解析 由三视图知，商鞅铜方升是由一个圆柱和一个长方体组合而成的，利用体积及已知线段长度即可求出x.故其体积为(5.4－x)×3×1＋π×eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)))2×x＝16.2－3x＋eq \f(1,4)πx＝12.6，又π＝3，故x＝1.6.故选B.
10．如图所示是某一容器的三视图，现向容器中匀速注水，容器中水面的高度h随时间t变化的可能图象是( )
答案 B
解析 根据所给的三视图可知原几何体是倒放的圆锥，设圆锥的底面半径为R，高为H，水流的速度是v，则由题意得vt＝eq \f(1,3)πeq \b\lc\(\rc\)(\a\vs4\al\c1(\f(h,H)))2R2h.当vt>0时，解得h＝eq \r(3,\f(3vH2t,πR2))，这是一个幂型函数，所以容器中水面的高度h随时间t变化的图象类似于幂函数y＝eq \r(3,x)的图象，故选B.
二、填空题
11．如图所示，正方形O′A′B′C′的边长为1 cm，它是水平放置的一个平面图形的直观图，则原图形的周长是________cm.
答案 8
解析 根据直观图的画法可知，在原几何图形中，OABC为平行四边形，且有OB⊥OA，OB＝2eq \r(2)，OA＝1，所以AB＝3.从而原图的周长为8 cm.
12．如图，点O为正方体ABCD－A′B′C′D′的中心，点E为平面B′BCC′的中心，点F为B′C′的中点，则空间四边形D′OEF在该正方体的各个面上的投影可能是 (填出所有可能的序号)．
答案 ①②③
解析 空间四边形D′OEF在正方体的平面DCC′D′上的投影是①；在平面BCC′B′上的投影是②；在平面ABCD上的投影是③，而不可能出现的投影为④的情况．
13．一四面体的三视图如图所示，则该四面体四个面中最大的面积是________．
答案 2eq \r(3)
解析 由三视图可知该四面体为D－BD1C1，由直观图可知面积最大的面为△BDC1.在正三角形BDC1中，BD＝2eq \r(2)，所以面积S＝eq \f(1,2)×(2eq \r(2))2×eq \f(\r(3),2)＝2eq \r(3).
14．某四面体的三视图如图所示．该四面体的六条棱的长度中，最大的是________．
答案 2eq \r(7)
解析
由三视图可知该四面体为V－ABC，如图所示．其中AE⊥BE，VC⊥平面ABE.EC＝CB＝2，AE＝2eq \r(3)，VC＝2，所以VB2＝VC2＋CB2＝8，VB＝2eq \r(2)，AC2＝AE2＋EC2＝(2eq \r(3))2＋22＝16，所以VA2＝AC2＋VC2＝16＋22＝20，VA＝eq \r(20)＝2eq \r(5).AB2＝AE2＋EB2＝(2eq \r(3))2＋42＝28，所以AB＝eq \r(28)＝2eq \r(7)>2eq \r(5)>2eq \r(2)，所以该四面体的六条棱的长度中，最大的为2eq \r(7).
三、解答题
15．已知正三棱锥V－ABC的正视图、侧视图和俯视图如图所示．
(1)画出该三棱锥的直观图；
(2)求出侧视图的面积．
解 (1)如右图所示．
(2)根据三视图间的关系可得BC＝2eq \r(3)，
∴侧视图中VA＝eq \r(42－\b\lc\(\rc\)(\a\vs4\al\c1(\f(2,3)×\f(\r(3),2)×2\r(3)))2)＝2eq \r(3).
∴S△VBC＝eq \f(1,2)×2eq \r(3)×2eq \r(3)＝6.
16．已知某几何体的俯视图是如图所示的矩形，正视图(或称主视图)是一个底边长为8，高为4的等腰三角形，侧视图(或称左视图)是一个底边长为6，高为4的等腰三角形．
(1)求该几何体的体积V；
(2)求该几何体的侧面积S.
解 由正视图和侧视图的三角形结合俯视图可知该几何体是一个底面为矩形，高为4，顶点在底面的射影是矩形中心的四棱锥，如图．
(1)V＝eq \f(1,3)×(8×6)×4＝64.
(2)四棱锥的两个侧面VAD，VBC是全等的等腰三角形，取BC的中点E，连接OE，VE，则△VOE为直角三角形，VE为△VBC边上的高，VE＝ eq \r(VO2＋OE2)＝4eq \r(2).
同理侧面VAB、VCD也是全等的等腰三角形，
AB边上的高h＝ eq \r(42＋\b\lc\(\rc\)(\a\vs4\al\c1(\f(6,2)))2)＝5.
∴S侧＝2×eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)×6×4\r(2)＋\f(1,2)×8×5))＝40＋24eq \r(2).