2022届高考数学理一轮复习新人教版课件：第二章函数导数及其应用第五节指数函数

这是一份2022届高考数学理一轮复习新人教版课件：第二章函数导数及其应用第五节指数函数，共60页。PPT课件主要包含了xn＝a，无意义，ar＋s，ars，arbr，0＋∞，y＝1，y＞1，＜y＜1，答案a＞c＞b等内容，欢迎下载使用。
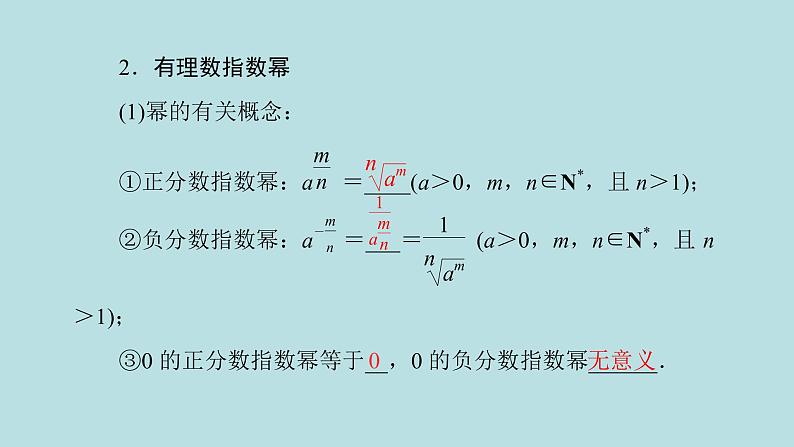
(2)有理数指数幂的运算性质：①aras＝____(a＞0，r，s∈Q)；②(ar)s＝____(a＞0，r，s∈Q)；③(ab)r＝_____(a＞0，b＞0，r∈Q).
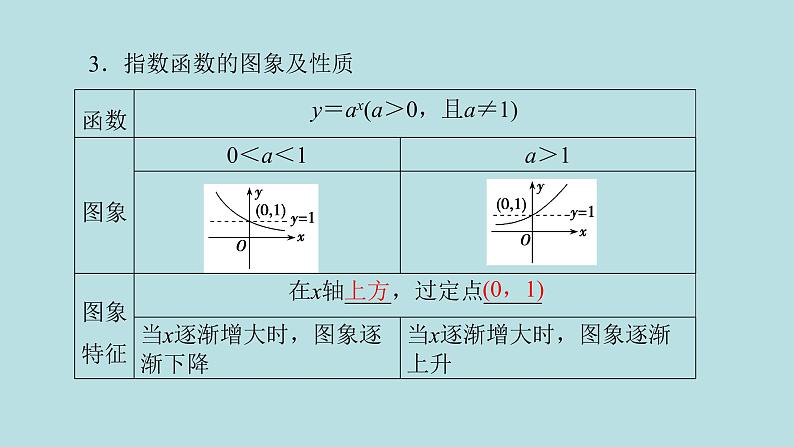
3．指数函数的图象及性质
3．指数函数的图象与底数大小的比较下图是指数函数(1)y＝ax，(2)y＝bx，(3)y＝cx，(4)y＝dx的图象，底数a，b，c，d与1之间的大小关系为c＞d＞1＞a＞b.规律：在y轴右(左)侧图象越高(低)，其底数越大．
4．指数函数图象的对称规律函数y＝ax的图象与y＝a－x的图象关于y轴对称，y＝ax的图象与y＝－ax的图象关于x轴对称，y＝ax的图象与y＝－a－x的图象关于坐标原点对称．
2．(基本方法：作指数函数图象)函数f(x)＝1－ex的图象大致是(　　)
3．(基本能力：研究函数性质)函数y＝(ax＋1)ex过定点________．答案：(0，1)
方法总结 1．这种循环根式型的化简，一般由里向外，将根式化为分数指数幂进行运算．2．指数幂运算的一般原则：(1)有括号的先算括号里的，无括号的先做指数运算．(2)先乘除后加减，负指数幂化成正指数幂的倒数．(3)底数是负数，先确定符号；底数是小数，先化成分数；底数是带分数的，先化成假分数．(4)若是根式，应化为分数指数幂，尽可能用幂的形式来表示，运用指数幂的运算性质来解答．　　
　　[典例剖析][典例]　(1)(2021·河北武邑中学调研)函数y＝e－|x－1|的大致图象是(　　)解析：当x＝1时，y＝1，排除选项CD.当x＞1时，y＝e－(x－1)为减函数，排除选项A.
(2)函数f(x)＝ax－b的图象如图所示，其中a，b为常数，则下列结论正确的是(　　)A．a＞1，b1，b>0C．0