初中数学冀教版九年级下册第29章 直线与圆的位置关系综合与测试优秀课后复习题

这是一份初中数学冀教版九年级下册第29章 直线与圆的位置关系综合与测试优秀课后复习题，共32页。试卷主要包含了下列说法正确的是，下列四个命题中，真命题是等内容，欢迎下载使用。
九年级数学下册第二十九章直线与圆的位置关系必考点解析
考试时间：90分钟；命题人：数学教研组
考生注意：
1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟
2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。
第I卷（选择题 30分）
一、单选题（10小题，每小题3分，共计30分）
1、如图，PA，PB是⊙O的切线，A，B是切点，点C为⊙O上一点，若∠ACB＝70°，则∠P的度数为（ ）

A．70° B．50° C．20° D．40°
2、已知⊙O的半径为4，，则点A在（ ）
A．⊙O内 B．⊙O上 C．⊙O外 D．无法确定
3、一个正多边形的半径与边长相等，则这个正多边形的边数为（　　）
A．4 B．5 C．6 D．8
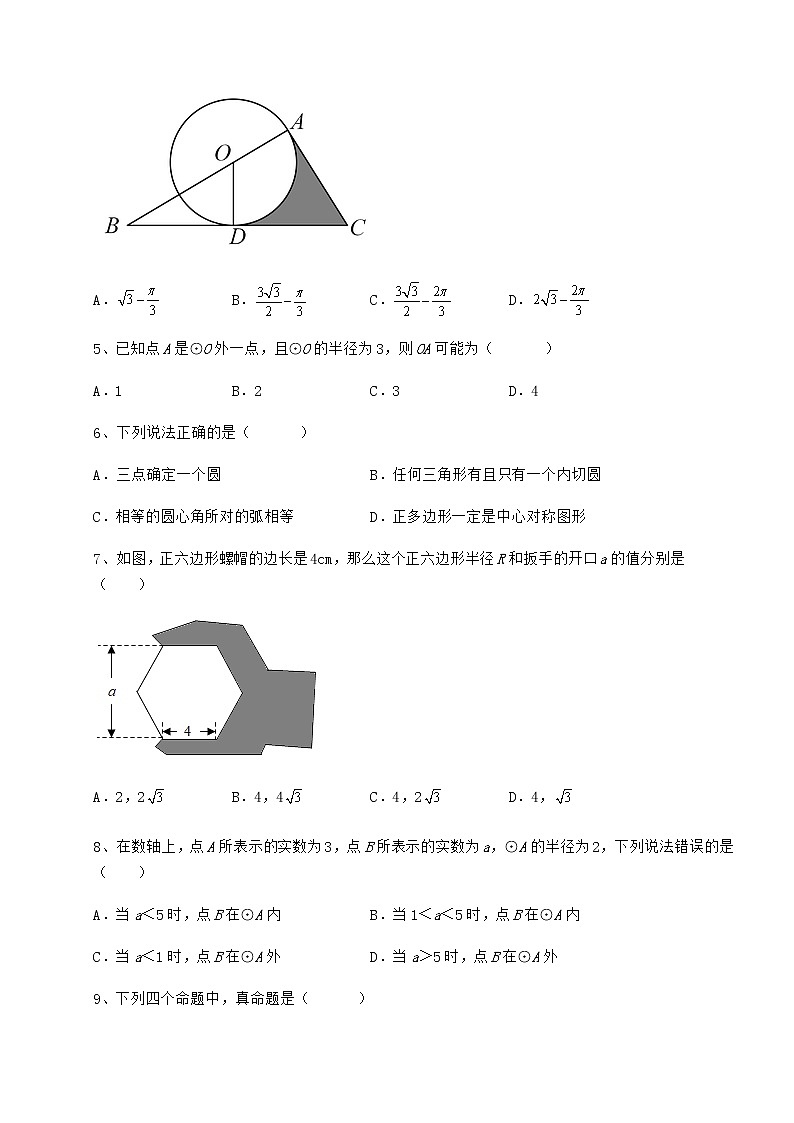
4、如图，在Rt△ABC中，，，，以边上一点为圆心作，恰与边，分别相切于点，，则阴影部分的面积为（ ）

A． B． C． D．
5、已知点A是⊙O外一点，且⊙O的半径为3，则OA可能为（ ）
A．1 B．2 C．3 D．4
6、下列说法正确的是（ ）
A．三点确定一个圆 B．任何三角形有且只有一个内切圆
C．相等的圆心角所对的弧相等 D．正多边形一定是中心对称图形
7、如图，正六边形螺帽的边长是4cm，那么这个正六边形半径R和扳手的开口a的值分别是（　　）

A．2，2 B．4，4 C．4，2 D．4，
8、在数轴上，点A所表示的实数为3，点B所表示的实数为a，⊙A的半径为2，下列说法错误的是（　　）
A．当a＜5时，点B在⊙A内 B．当1＜a＜5时，点B在⊙A内
C．当a＜1时，点B在⊙A外 D．当a＞5时，点B在⊙A外
9、下列四个命题中，真命题是（ ）
A．相等的圆心角所对的两条弦相等 B．三角形的内心是到三角形三边距离相等的点
C．平分弦的直径一定垂直于这条弦 D．等弧就是长度相等的弧
10、如图，正方形ABCD的边长为8，若经过C，D两点的⊙O与直线AB相切，则⊙O的半径为（ ）

A．4.8 B．5 C．4 D．4
第Ⅱ卷（非选择题 70分）
二、填空题（5小题，每小题4分，共计20分）
1、如图，在△ABC中，AC＝BC，点O在AB上，以OA为半径的圆O与BC相切于点C，∠B＝_________．

2、如图，为的直径，、为上的点，连接、、、，为延长线上一点，连接，且，．若的半径为，则点到的距离为________．

3、是的内接正六边形一边，点是优弧上的一点（点不与点，重合）且，与交于点，则的度数为_______．

4、如图，在△ABC中，∠ACB＝90°，CD＝2，以CD为直径的⊙与AB相切于点E．若弧DE的长为为π，则阴影部分的面积为 _____．（保留π）

5、如图，正方形ABCD的边长为1，⊙O经过点C，CM为⊙O的直径，且CM＝1．过点M作⊙O的切线分别交边AB，AD于点G，H．BD与CG，CH分别交于点E，F，⊙O绕点C在平面内旋转（始终保持圆心O在正方形ABCD内部）．给出下列四个结论：
①HD＝2BG；②∠GCH＝45°；③H，F，E，G四点在同一个圆上；④四边形CGAH面积的最大值为2．其中正确的结论有 _____（填写所有正确结论的序号）．

三、解答题（5小题，每小题10分，共计50分）
1、如图，在△ABC中，∠ACB＝90°，AC＝BC，O点在△ABC内部，⊙O经过B、C两点且交AB于点D，连接CO并延长交线段AB于点G，以GD、GC为邻边作平行四边形GDEC．

(1)求证：直线DE是⊙O的切线；
(2)若DE＝7，CE＝5，求⊙O的半径．
2、如图，已知是的直径，点在上，点在外．

(1)动手操作：作的角平分线，与圆交于点（要求：尺规作图，不写作法，保留作图痕迹）
(2)综合运用，在你所作的图中．若，求证：是的切线．
3、如图，四边形OAEC是平行四边形，以O为圆心，OC为半径的圆交CE于D，延长CO交O于B，连接AD、AB，AB是O的切线．

(1)求证：AD是O的切线．
(2)若O的半径为4，，求平行四边形OAEC的面积．
4、如图，直线MN交⊙O于A，B两点，AC是直径，AD平分∠CAM交⊙O于D，过D作DE⊥MN于E．

(1)求证：DE是⊙O的切线；
(2)若DE＝8，AE＝6，求⊙O的半径．
5、如图，在平面直角坐标系xOy中，点A与点B的坐标分别是（1，0），（7，0）．

(1)对于坐标平面内的一点P，给出如下定义：如果∠APB＝45°，那么称点P为线段AB的“完美点”．
①设A、B、P三点所在圆的圆心为C，则点C的坐标是 　 　，⊙C的半径是 　 　；
②y轴正半轴上是否有线段AB的“完美点”？如果有，求出“完美点”的坐标；如果没有，请说明理由；
(2)若点P在y轴负半轴上运动，则当∠APB的度数最大时，点P的坐标为 　 　．

-参考答案-
一、单选题
1、D
【解析】
【分析】
首先连接OA，OB，由PA，PB为⊙O的切线，根据切线的性质，即可得∠OAP=∠OBP=90°，又由圆周角定理，可求得∠AOB的度数，继而可求得答案．
【详解】
解：连接OA，OB，

∵PA，PB为⊙O的切线，
∴∠OAP=∠OBP=90°，
∵∠ACB=70°，
∴∠AOB=2∠P=140°，
∴∠P=360°-∠OAP-∠OBP-∠AOB=40°．
故选：D．
【点睛】
此题考查了切线的性质与圆周角定理，注意掌握辅助线的作法和数形结合思想的应用．
2、C
【解析】
【分析】
根据⊙O的半径r=4，且点A到圆心O的距离d=5知d>r，据此可得答案．
【详解】
解：∵⊙O的半径r=4，且点A到圆心O的距离d=5，
∴d>r，
∴点A在⊙O外，
故选：C．
【点睛】
本题主要考查点与圆的位置关系，点与圆的位置关系有3种．设⊙O的半径为r，点P到圆心的距离OP=d，则有：①点P在圆外⇔d＞r；②点P在圆上⇔d=r；③点P在圆内⇔d＜r．
3、C
【解析】
【分析】
如图（见解析），先根据等边三角形的判定与性质可得，再根据正多边形的中心角与边数的关系即可得．
【详解】
解：如图，由题意得：，
是等边三角形，
，
则这个正多边形的边数为，
故选：C．

【点睛】
本题考查了正多边形，熟练掌握正多边形的中心角与边数的关系是解题关键．
4、A
【解析】
【分析】
连结OC，根据切线长性质DC=AC，OC平分∠ACD，求出∠OCD=∠OCA==30°，利用在Rt△ABC中，AC=ABtanB=3×，在Rt△AOC中，∠ACO=30°，AO=ACtan30°=，利用三角形面积公式求出，，再求出扇形面积，利用割补法求即可．
【详解】
解：连结OC，
∵以边上一点为圆心作，恰与边，分别相切于点A, ，
∴DC=AC，OC平分∠ACD，
∵，，
∴∠ACD=90°-∠B=60°，
∴∠OCD=∠OCA==30°，
在Rt△ABC中，AC=ABtanB=3×，
在Rt△AOC中，∠ACO=30°，AO=ACtan30°=，
∴OD=OA=1，DC=AC=，
∴，，
∵∠DOC=360°-∠OAC-∠ACD-∠ODC=360°-90°-90°-60°=120°，
∴，
S阴影=．
故选择A．

【点睛】
本题考查切线长性质，锐角三角形函数，扇形面积，三角形面积，角的和差计算，割补法求阴影面积，掌握切线长性质，锐角三角形函数，扇形面积，三角形面积，角的和差计算，割补法求阴影面积是解题关键．
5、D
【解析】
【分析】
根据点到圆心的距离和圆的半径之间的数量关系，即可判断点和圆的位置关系．点到圆心的距离小于圆的半径，则点在圆内；点到圆心的距离等于圆的半径，则点在圆上；点到圆心的距离大于圆的半径，则点在圆外．
【详解】
解：∵点A为⊙O外的一点，且⊙O的半径为3，
∴线段OA的长度＞3．
故选：D．
【点睛】
此题考查了点和圆的位置关系与数量之间的联系：点到圆心的距离大于圆的半径，则点在圆外．
6、B
【解析】
【分析】
根据确定圆的条件、三角形的内切圆、圆心角化和弧的关系、中心对称图形的概念判断．
【详解】
解：A、不在同一直线上的三点确定一个圆，故错误；
B、任何三角形有且只有一个内切圆，正确；
C、在同圆或等圆中，相等的圆心角所对的弧相等，故错误；
D、边数是偶数的正多边形一定是中心对称图形，故错误；
故选：B．
【点睛】
本题考查的是命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题．判断命题的真假关键是要熟悉课本中的性质定理．
7、B
【解析】
【分析】
根据正六边形的内角度数可得出∠BAD=30°，为等边三角形，得BC=2AB，再通过解直角三角形即可得出a的值，进而可求出a的值，此题得解．
【详解】
解：如图，

∵正六边形的任一内角为120°，
∴∠ABD=180°-120°=60°，
∴∠BAD=30°，为等边三角形，
∵
∴
∴
∴
∴这个正六边形半径R和扳手的开口a的值分别是4，4．
故选：B．
【点睛】
本题考查了正多边形以及勾股定理，牢记正多边形的内角度数是解题的关键．
8、A
【解析】
【分析】
根据数轴以及圆的半径可得当d=r时，⊙A与数轴交于两点：1、5，进而根据点到圆心的距离与半径比较即可求得点与圆的位置关系，进而逐项分析判断即可
【详解】
解：∵圆心A在数轴上的坐标为3，圆的半径为2，
∴当d=r时，⊙A与数轴交于两点：1、5，
故当a=1、5时点B在⊙A上；
当d＜r即当1＜a＜5时，点B在⊙A内；
当d＞r即当a＜1或a＞5时，点B在⊙A外．
由以上结论可知选项B、C、D正确，选项A错误．
故选A．
【点睛】
本题考查了数轴，点与圆的位置关系，掌握点与圆的位置关系是解题的关键．
9、B
【解析】
【分析】
利用圆的有关性质及定理、三角形的内心的性质、垂径定理等知识分别判断后即可确定正确的选项．
【详解】
解：A、同圆或等圆中，相等的圆心角所对的两条弦相等，则原命题是假命题，故本选项不符合题意；
B、三角形的内心是到三角形三边距离相等的点，是真命题，故本选项符合题意；
C、平分弦（不是直径）的直径一定垂直于这条弦，则原命题是假命题，故本选项不符合题意；
D、等弧是能够完全重合的弧，长度相等的弧不一定是等弧，则原命题是假命题，故本选项不符合题意；
故选：B
【点睛】
本题主要考查了命题与定理的知识，解题的关键是了解圆的有关性质及定理、三角形的内心的性质、垂径定理等知识，难度不大．
10、B
【解析】
【分析】
连接EO，延长EO交CD于F，连接DO，设半径为x．构建方程即可解决问题．
【详解】
解：设⊙O与AB相切于点E．连接EO，延长EO交CD于F，连接DO，
再设⊙O的半径为x．

∵AB切⊙O于E，
∴EF⊥AB，
∵AB∥CD，
∴EF⊥CD，
∴∠OFD=90°，
在Rt△DOF中，∵∠OFD=90°，OF2+DF2=OD2，
∴（8-x）2+42= x2，
∴x=5，
∴⊙O的半径为5．
故选：B．
【点睛】
本题考查了切线的性质、正方形的性质、垂径定理、勾股定理等知识，解题的关键是灵活运用这些知识解决问题，学会添加常用辅助线，构造直角三角形解决问题．
二、填空题
1、30°##30度
【解析】
【分析】
连接OC，如图，利用切线的性质得到∠BCO=90°，再由CA=CB得到∠B=∠A，利用圆周角定理得到∠BOC=2∠A，则可根据三角形内角和计算出∠B=30°．
【详解】
解：连接OC，如图，

∵⊙O与BC相切于点C，
∴OC⊥BC，
∴∠BCO=90°，
∵CA=CB，
∴∠B=∠A，
∵∠BOC=2∠A，
而∠B+∠BOC=90°，
∴∠B+2∠B=90°，解得∠B=30°，
故答案为：30°．
【点睛】
本题考查了切线的性质：圆的切线垂直于经过切点的半径．也考查了等腰三角形的性质和圆周角定理．
2、##
【解析】
【分析】
连接OC，证明CD⊥OC；运用勾股定理求出OD=10，过点A作AF⊥DC，交DC延长线于点F，过点C作CG⊥AD于点G，在Rt△OCD中运用等积关系求出CD，同理，在△ACD中运用等积关系可求出AF
【详解】
解：连接OC，

∵AB是圆的直径，
∴
∴
∵
∴
∵
∴
∴
∴，即OC⊥CD
∵的半径为
∴

在Rt△OCD中，
∴
∴
过点A作AF⊥DC，交DC延长线于点F，过点C作CG⊥AD于点G，
∵
∴，解得，
同理：
∴
∴
故答案为：
【点睛】
本题考查了切线的判定、三角形面积、勾股定理等知识，解题的关键是作辅助线，构造直角三角形．
3、90°
【解析】
【分析】
先根据是的内接正六边形一边得，再根据圆周角性质得，再根据平行线的性质得,最后由三角形外角性质可得结论．
【详解】
解：∵是的内接正六边形一边
∴
∴
∵
∴
∴
故答案为90°
【点睛】
本题主要考查了正多边形与圆，圆周角定理等知识，熟练掌握相关定理是解答本题的关键
4、
【解析】
【分析】
连接OE，首先由弧长公式求得∠EOD＝60°；然后利用△BEO的性质得到线段OB的长度，易得AC与BC的长度；最后根据S阴影＝S△ABC﹣S扇形OCE﹣S△OBE解答．
【详解】
解：如图，连接OE，
∵以CD为直径的⊙与AB相切于点E，
∴OE⊥BE．
设∠EOD＝n°，
∵OD＝ CD＝1，弧DE的长为π，
∴＝π．
∴∠EOD＝60°．
∴∠B＝30°，∠COE＝120°．
∴OB＝2OE＝2，BE＝，AB＝2AC，
∵AC＝AE，
∴AC＝BE＝．
∴S阴影＝S△ABC﹣S扇形OCE﹣S△OBE
＝××3﹣﹣×1×＝﹣．
故答案是：﹣．

【点睛】
考查了切线的性质，弧长的计算和扇形面积的计算，若出现圆的切线，必连过切点的半径，构造定理图，得出垂直关系．简记作：见切点，连半径，见垂直．
5、②③④
【解析】
【分析】
根据切线的性质，正方形的性质，通过三角形全等，证明HD=HM，∠HCM=∠HCD，GM=GB，∠GCB=∠GCM，可判断前两个结论；运用对角互补的四边形内接于圆，证明∠GHF+∠GEF=180°，取GH的中点P，连接PA，则PA+PC≥AC，当PC最大时，PA最小，根据直径是圆中最大的弦，故PC=1时，PA最小，计算即可．
【详解】
∵GH是⊙O的切线，M为切点，且CM是⊙O的直径，
∴∠CMH=90°，
∵四边形ABCD是正方形，
∴∠CMH=∠CDH=90°，
∵CM=CD，CH=CH，
∴△CMH≌△CDH，
∴HD=HM，∠HCM=∠HCD，
同理可证，∴GM=GB，∠GCB=∠GCM，
∴GB+DH=GH，无法确定HD＝2BG，
故①错误；
∵∠HCM+∠HCD+∠GCB+∠GCM=90°，
∴2∠HCM+2∠GCM=90°，
∴∠HCM+∠GCM=45°，
即∠GCH＝45°，
故②正确；

∵△CMH≌△CDH，BD是正方形的对角线，
∴∠GHF=∠DHF，∠GCH=∠HDF=45°，
∴∠GHF+∠GEF=∠DHF +∠GCH+∠EFC
=∠DHF +∠HDF+∠HFD
=180°，
根据对角互补的四边形内接于圆，
∴H，F，E，G四点在同一个圆上，
故③正确；
∵正方形ABCD的边长为1，
∴
=1
=，∠GAH=90°，AC=
取GH的中点P，连接PA，
∴GH=2PA，
∴=，
∴当PA取最小值时，有最大值，
连接PC，AC，
则PA+PC≥AC，
∴PA≥AC- PC，
∴当PC最大时，PA最小，
∵直径是圆中最大的弦，
∴PC=1时，PA最小，
∴当A，P，C三点共线时，且PC最大时，PA最小，
∴PA=-1，
∴最大值为：1-（-1）=2-，
∴四边形CGAH面积的最大值为2，
∴④正确；
故答案为: ②③④．
【点睛】
本题考查了切线的性质，直径是最大的弦，三角形的全等，直角三角形斜边上的中线，四点共圆，正方形的性质，熟练掌握圆的性质，灵活运用直角三角形的性质，线段最短原理是解题的关键．
三、解答题
1、 (1)见解析
(2)4
【解析】
【分析】
（1）连接OD，根据题意和平行四边形的性质可得DE∥CG，可得OD⊥DE，即可求解；
（2）设⊙O的半径为r，因为∠GOD＝90°，根据勾股定理可求解r，当r＝2时，OG＝5，此时点G在⊙O外，不合题意，舍去，可求解．
(1)
证明：连接OD，

∵∠ACB＝90°，AC＝BC，
∴∠ABC＝45°，
∴∠COD＝2∠ABC＝90°，
∵四边形GDEC是平行四边形，
∴DE∥CG，
∴∠ODE+∠COD＝180°，
∴∠ODE＝90°，即OD⊥DE，
∵OD是半径，
∴直线DE是⊙O的切线；
(2)
解：设⊙O的半径为r，
∵四边形GDEC是平行四边形，
∴CG＝DE＝7，DG＝CE＝5，
∵∠GOD＝90°，
∴OD2+OG2＝DG2，即r2+（7﹣r）2＝52，
解得：r1＝3，r2＝4，
当r＝3时，OG＝4＞3，此时点G在⊙O外，不合题意，舍去，
∴r＝4，即⊙O的半径4．
【点睛】
本题主要考查了平行四边形的性质，切线的性质和判定，勾股定理，熟练掌握切线的判定定理是解决本题的关键．
2、 (1)作图见解析
(2)证明见解析
【解析】
【分析】
（1）如图，以点C为圆心BC为半径画弧交AC于点M；以B、M为圆心，大于为半径画弧，交点为N，连接CN交于点D即可．
（2）连接AD ， ，，，，AB为直径，进而可得AE是的切线．
(1)
解：如图，以点C为圆心BC为半径画弧交AC于点M；以B、M为圆心，大于为半径画弧，交点为N，连接CN交于点D．

(2)
解：连接AD，如图

∵为直径
∴
∵
∴
∴
又∵AB为直径
∴AE是的切线．
【点睛】
本题考查了角平分线的画法，圆周角，切线的判定等知识．解题的关键在于对知识的灵活熟练的运用．
3、 (1)见解析
(2)32
【解析】
【分析】
（1）连接OD，证明，可得，根据切线的性质可得，进而可得，即可证明AD是O的切线；
（2）根据平行四边形OAEC的面积等于2倍即可求解．
(1)
证明：连接OD．

∵四边形OAEC是平行四边形，
∴，




又∵，

∴，
∵AB与相切于点B，


∴，

又∵OD是的半径，
∴AD为的切线．
(2)
∵

在Rt△AOD中，
∴平行四边形OABC的面积是
【点睛】
本题考查了切线的性质与判定，平行四边形的性质，三角形全等的性质与判定，掌握切线的性质与判定是解题的关键．
4、 (1)见解析
(2)
【解析】
【分析】
（1）连接OD，根据等腰三角形的性质和角平分线定义证得∠ODA＝∠DAE，可证得DO∥MN，根据平行线的性质和切线的判定即可证的结论；
（2）连接CD，先由勾股定理求得AD，连接CD，根据圆周角定理和相似三角形的判定证明△ACD∽△ADE，然后根据相似三角形的性质求解AC即可求解．
(1)
证明：连接OD，
∵OA＝OD，
∴∠OAD＝∠ODA，
∵AD平分∠CAM，∠OAD＝∠DAE，
∴∠ODA＝∠DAE，
∴DO∥MN，
∵DE⊥MN，
∴DE⊥OD，
∵D在⊙O上，
∴DE是⊙O的切线；
(2)
解：∵∠AED＝90°，DE＝8，AE＝6，
∴AD＝＝10，
连接CD，∵AC是⊙O的直径，
∴∠ADC＝∠AED＝90°，
∵∠CAD＝∠DAE，
∴△ACD∽△ADE，
∴，即，
∴AC＝，
∴⊙O的半径是．

【点睛】
本题考查等腰三角形的性质、角平分线的定义、平行线的判定与性质、切线的判定、勾股定理、圆周角定理、相似三角形的判定与性质等知识，熟练掌握相关知识的联系与运用是解答的关键．
5、 (1)①(4,3)或C(4，−3)，，②，
(2)
【解析】
【分析】
（1）①在x轴的上方，作以AB为斜边的等腰直角三角形△ACB，易知A，B，P三点在⊙C上，圆心C的坐标为(4,3)，半径为3，根据对称性可知点C(4，−3)也满足条件；②当圆心为C（4，3）时，过点C作CD⊥y轴于D，则D（0，3），CD=4，根据⊙C的半径得⊙C与y轴相交，设交点为，，此时，在y轴的正半轴上，连接、、CA，则==CA =r=3，得，即可得；
（2）如果点P在y轴的负半轴上，设此时圆心为E，则E在第四象限，在y轴的负半轴上任取一点M(不与点P重合)，连接MA，MB，PA，PB，设MB交于⊙E于点N，连接NA，则∠APB=∠ANB，∠ANB是△MAN的外角，∠ANB>∠AMB，即∠APB>∠AMB，过点E作EF⊥x轴于F，连接EA，EP，则AF=AB=3，OF=4，四边形OPEF是矩形，OP=EF，PE=OF=4，得，则，即可得．
(1)
①如图1中，

在x轴的上方，作以AB为斜边的等腰直角三角形△ACB，易知A，B，P三点在⊙C上，
圆心C的坐标为(4,3)，半径为3，
根据对称性可知点C(4,−3)也满足条件，
故答案是：(4,3)或C(4，−3)，，
②y轴的正半轴上存在线段AB的“等角点”。
如图2所示，当圆心为C（4，3）时，过点C作CD⊥y轴于D，则D（0，3），CD=4，

∵⊙C的半径，
∴⊙C与y轴相交，
设交点为，，此时，在y轴的正半轴上，
连接、、CA，则==CA =r=3，
∵CD⊥y轴，CD=4，，
∴，
∴，；
当圆心为C（4，-3）时，点P在y轴的负半轴上，不符合题意；
故答案为：，
(2)
当过点A，B的圆与y轴负半轴相切于点P时，∠APB最大，理由如下：
如果点P在y轴的负半轴上，设此时圆心为E，则E在第四象限，
如图3所示，在y轴的负半轴上任取一点M(不与点P重合)，
连接MA，MB，PA，PB，设MB交于⊙E于点N，连接NA，

∵点P，点N在⊙E上，
∴∠APB=∠ANB，
∵∠ANB是△MAN的外角，
∴∠ANB>∠AMB，
即∠APB>∠AMB，
此时，过点E作EF⊥x轴于F，连接EA，EP，则AF=AB=3，OF=4，
∵⊙E与y轴相切于点P，则EP⊥y轴，
∴四边形OPEF是矩形，OP=EF，PE=OF=4，
∴⊙E的半径为4，即EA=4，
∴在Rt△AEF中，，
∴，
即 ．
故答案为：
【点睛】
本题考查了圆与三角形，勾股定理，三角形的外角，矩形的性质，解题的关键是掌握这些知识点．