数学九年级下册第29章 直线与圆的位置关系综合与测试精品练习题

这是一份数学九年级下册第29章 直线与圆的位置关系综合与测试精品练习题，共35页。

九年级数学下册第二十九章直线与圆的位置关系定向测评
考试时间：90分钟；命题人：数学教研组
考生注意：
1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟
2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。
第I卷（选择题 30分）
一、单选题（10小题，每小题3分，共计30分）
1、如图，PA、PB是的切线，A、B为切点，连接OB、AB，若，则的度数为（ ）

A．50° B．55° C．65° D．70°
2、如图，正五边形ABCDE内接于⊙O，则∠CBD的度数是（　　）

A．30° B．36° C．60° D．72°
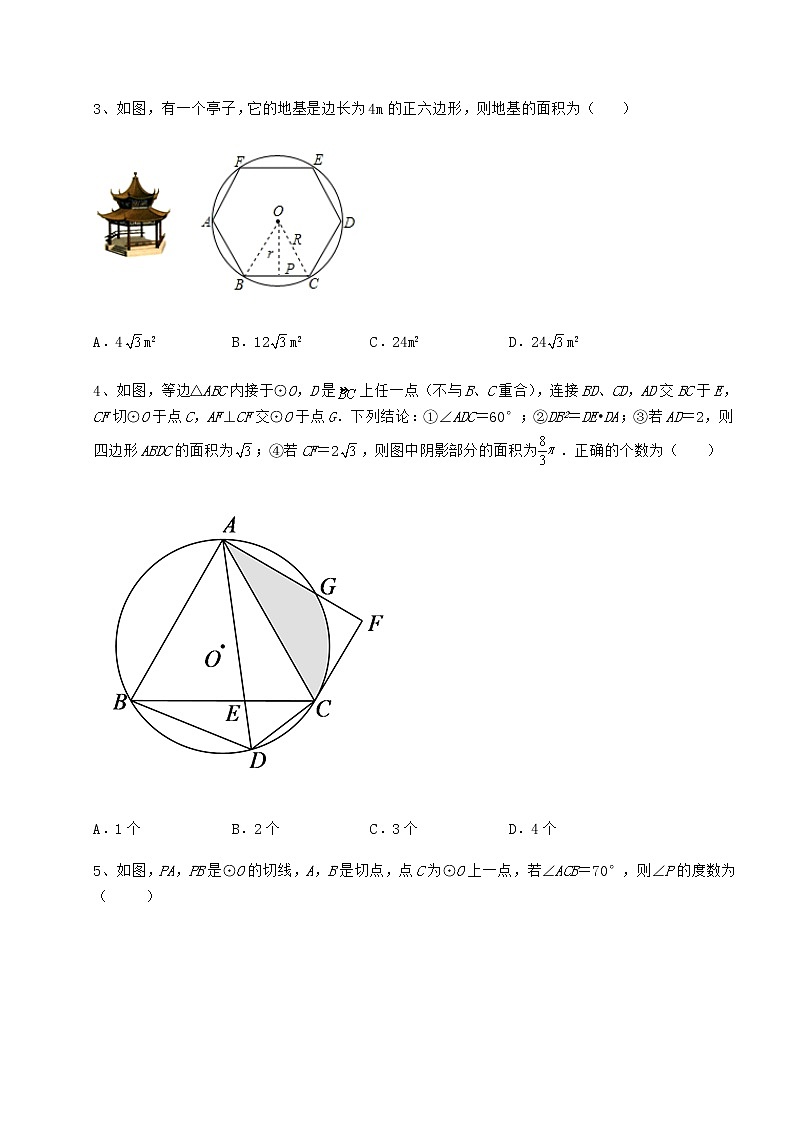
3、如图，有一个亭子，它的地基是边长为4m的正六边形，则地基的面积为（　　）

A．4m2 B．12m2 C．24m2 D．24m2
4、如图，等边△ABC内接于⊙O，D是上任一点（不与B、C重合），连接BD、CD，AD交BC于E，CF切⊙O于点C，AF⊥CF交⊙O于点G．下列结论：①∠ADC＝60°；②DB2＝DE•DA；③若AD＝2，则四边形ABDC的面积为；④若CF＝2，则图中阴影部分的面积为．正确的个数为（　　）

A．1个 B．2个 C．3个 D．4个
5、如图，PA，PB是⊙O的切线，A，B是切点，点C为⊙O上一点，若∠ACB＝70°，则∠P的度数为（ ）

A．70° B．50° C．20° D．40°
6、已知正三角形外接圆半径为，这个正三角形的边长是（ ）
A． B． C． D．
7、已知的半径为5cm，点P到圆心的距离为4cm，则点P和圆的位置关系（ ）
A．点在圆内 B．点在圆外 C．点在圆上 D．无法判断
8、如图，AB是⊙O的直径，点M在BA的延长线上，MA＝AO，MD与⊙O相切于点D，BC⊥AB交MD的延长线于点C，若⊙O的半径为2，则BC的长是（　　）

A．4 B． C． D．3
9、在同一平面内，有一半径为6的⊙O和直线m，直线m上有一点P，且OP=4；则直线m与⊙O的位置关系是 （ ）
A．相交 B．相离 C．相切 D．不能确定
10、已知半径为5的圆，直线l上一点到圆心的距离是5，则直线和圆的位置关系为（ ）
A．相切 B．相离 C．相切或相交 D．相切或相离
第Ⅱ卷（非选择题 70分）
二、填空题（5小题，每小题4分，共计20分）
1、《九章算术》是我国古代的数学名著，书中有这样的一个问题：“今有勾八步，股十五步，问勾中容圆径几何？”．其意思是：“如图，现有直角三角形，勾（短直角边）长为 8 步，股（长直角边）长为 15 步，问该直角三角形所能容纳的最大圆的直径是多少？”答：该直角三角形所能容纳的最大圆的直径是______步．

2、如图，点，，均在的正方形网格格点上，过，，三点的外接圆除经过，，三点外还能经过的格点数为_________．

3、如图，AB是⊙O的直径，AC是⊙O的弦，过点C的切线交AB的延长线于点D．若∠A=30°，则∠D的度数为______°．

4、如图，PA，PB是的切线，切点分别为A，B．若，，则AB的长为______．

5、如图，、是的切线，其中、为切点，点在上，，则______．

三、解答题（5小题，每小题10分，共计50分）
1、如图，中，．

(1)用直尺和圆规作，使圆心在边上，且与、所在直线相切（不写作法，保留作图痕迹）；
(2)在（1）的条件下，再从以下两个条件①“，的周长为12cm；②，”中选择一个作为条件，并求的半径．
2、苏科版教材八年级下册第94页第19题，小明在学过圆之后，对该题进行重新探究，请你和他一起完成问题探究．
【问题探究】小明把原问题转化为动点问题，如图1，在边长为6cm的正方形ABCD中，点E从点A出发，沿边AD向点D运动，同时，点F从点B出发，沿边BA向点A运动，它们的运动速度都是2cm/s，当点E运动到点D时，两点同时停止运动，连接CF、BE交于点M，设点E， F运动时问为t秒．

(1)【问题提出】如图1，点E，F分别在方形ABCD中的边AD、AB上，且，连接BE、CF交于点M，求证：．请你先帮小明加以证明．
(2)如图1，在点E、F的运动过程中，点M也随之运动，请直接写出点M的运动路径长 cm．
(3)如图2，连接CE，在点E、F的运动过程中．
①试说明点D在△CME的外接圆O上；
②若①中的O与正方形的各边共有6个交点，请直接写出t的取值范围．
3、如图，AB是ΘO的直径，弦AD平分∠BAC，过点D作DE⊥AC，垂足为E．

(1)判断DE所在直线与ΘO的位置关系，并说明理由；
(2)若AE＝4，ED＝2，求ΘO的半径．
4、如图，是的切线，点在上，与相交于，是的直径，连接，若．

(1)求证：平分；
(2)当，时，求的半径长．
5、如图，在中，，平分，与交于点，，垂足为，与交于点，经过，，三点的与交于点．

(1)求证是的切线；
(2)若，，求的半径．

-参考答案-
一、单选题
1、A
【解析】
【分析】
根据切线的性质得出PA=PB，∠PBO=90°，再根据三角形内角和定理求解即可．
【详解】
∵PA、PB是⊙O的切线，
∴PA=PB，∠OBP=90°，
又∵∠ABO=25°，
∴∠PBA=90°-25°=65°=∠PAB，
∴∠P=180°-65°-65°=50°，
故选：A．
【点睛】
本题考查切线的性质，三角形内角和定理，掌握切线的性质和等腰三角形的性质，三角形内角和为180°是解题的关键．
2、B
【解析】
【分析】
求出正五边形的一个内角的度数，再根据等腰三角形的性质和三角形的内角和定理计算即可．
【详解】
解：∵正五边形ABCDE中，
∴∠BCD==108°，CB=CD，
∴∠CBD=∠CDB=（180°-108°）=36°，
故选：B．
【点睛】
本题考查了正多边形和圆，求出正五边形的一个内角度数是解决问题的关键．
3、D
【解析】
【分析】
先根据等边三角形的性质求出△OBC的面积，然后由地基的面积是△OBC的6倍即可得到答案
【详解】
解：如图所示，正六边形ABCDEF，连接OB，OC，过点O作OP⊥BC于P，
由题意得：BC=4cm，
∵六边形ABCD是正六边形，
∴∠BOC=360°÷6=60°，
又∵OB=OC，
∴△OBC是等边三角形，
∴，，
∴，
∴，
∴，
故选D．

【点睛】
本题主要考查了正多边形和圆，等边三角形的性质与判定，勾股定理，熟知正多边形和圆的关系是解题的关键．
4、C
【解析】
【分析】
如图1，△ABC是等边三角形，则∠ABC＝60°，根据同弧所对的圆周角相等∠ADC＝∠ABC＝60°，所以判断①正确；如图1，可证明△DBE∽△DAC，则，所以DB•DC＝DE•DA，而DB与DC不一定相等，所以判断②错误；如图2，作AH⊥BD于点H，延长DB到点K，使BK＝CD，连接AK，先证明△ABK≌△ACD，可证明S四边形ABDC＝S△ADK，可以求得S△ADK＝，所以判断③正确；如图3，连接OA、OG、OC、GC，由CF切⊙O于点C得CF⊥OC，而AF⊥CF，所以AF∥OC，由圆周角定理可得∠AOC＝120°，则∠OAC＝∠OCA＝30°，于是∠CAG＝∠OCA＝30°，则∠COG＝2∠CAG＝60°，可证明△AOG和△COG都是等边三角形，则四边形OABC是菱形，因此OA∥CG，推导出S阴影＝S扇形COG，在Rt△CFG中根据勾股定理求出CG的长为4，则⊙O的半径为4，可求得S阴影＝S扇形COG＝＝，所以判断④正确，所以①③④这3个结论正确．
【详解】
解：如图1，∵△ABC是等边三角形，
∴∠ABC＝60°，
∵等边△ABC内接于⊙O，
∴∠ADC＝∠ABC＝60°，
故①正确；
∵∠BDE＝∠ACB＝60°，∠ADC＝∠ABC＝60°，
∴∠BDE＝∠ADC，
又∠DBE＝∠DAC，
∴△DBE∽△DAC，
∴,
∴DB•DC＝DE•DA，
∵D是上任一点，
∴DB与DC不一定相等，
∴DB•DC与DB2也不一定相等，
∴DB2与DE•DA也不一定相等，
故②错误；

如图2，作AH⊥BD于点H，延长DB到点K，使BK＝CD，连接AK，
∵∠ABK+∠ABD＝180°，∠ACD+∠ABD＝180°，
∴∠ABK＝∠ACD，
∴AB＝AC，
∴△ABK≌△ACD（SAS），
∴AK＝AD，S△ABK＝S△ACD，
∴DH＝KH＝DK，

∵∠AHD＝90°，∠ADH＝60°，
∴∠DAH＝30°，
∵AD＝2，
∴DH＝AD＝1，
∴DK＝2DH＝2，，
∴S△ADK＝，
∴S四边形ABDC＝S△ABD+S△ACD＝S△ABD+S△ABK＝S△ADK＝，
故③正确；
如图3，连接OA、OG、OC、GC，则OA＝OG＝OC，
∵CF切⊙O于点C，
∴CF⊥OC，
∵AF⊥CF，
∴AF∥OC，
∵∠AOC＝2∠ABC＝120°，
∴∠OAC＝∠OCA＝×（180°﹣120°）＝30°，
∴∠CAG＝∠OCA＝30°，
∴∠COG＝2∠CAG＝60°，
∴∠AOG＝60°，
∴△AOG和△COG都是等边三角形，
∴OA＝OC＝AG＝CG＝OG，
∴四边形OABC是菱形，
∴OA∥CG，
∴S△CAG＝S△COG，
∴S阴影＝S扇形COG，
∵∠OCF＝90°，∠OCG＝60°，
∴∠FCG＝30°，
∵∠F＝90°，
∴FG＝CG，
∵FG2+CF2＝CG2，CF＝，
∴（CG）2+（）2＝CG2，
∴CG＝4，
∴OC＝CG＝4，
∴S阴影＝S扇形COG＝＝，
故④正确，
∴①③④这3个结论正确，
故选C．

【点睛】
本题主要考查了等边三角形的性质与判定，圆切线的性质，圆周角定理，全等三角形的性质与判定，菱形的性质与判定，勾股定理，含30度角的直角三角形的性质等等，解题的关键在于能够熟练掌握相关知识进行求解．
5、D
【解析】
【分析】
首先连接OA，OB，由PA，PB为⊙O的切线，根据切线的性质，即可得∠OAP=∠OBP=90°，又由圆周角定理，可求得∠AOB的度数，继而可求得答案．
【详解】
解：连接OA，OB，

∵PA，PB为⊙O的切线，
∴∠OAP=∠OBP=90°，
∵∠ACB=70°，
∴∠AOB=2∠P=140°，
∴∠P=360°-∠OAP-∠OBP-∠AOB=40°．
故选：D．
【点睛】
此题考查了切线的性质与圆周角定理，注意掌握辅助线的作法和数形结合思想的应用．
6、B
【解析】
【分析】
如图， 为正三角形ABC的外接圆，过点O作OD⊥AB于点D，连接OA， 再由等边三角形的性质，可得∠OAB=30°，，然后根据锐角三角函数，即可求解．
【详解】
解：如图， 为正三角形ABC的外接圆，过点O作OD⊥AB于点D，连接OA，

根据题意得：OA= ，∠OAB=30°，，
在中，
，
∴AB=3，即这个正三角形的边长是3．
故选：B
【点睛】
本题主要考查了锐角三角函数，三角形的外接圆，熟练掌握锐角三角函数，三角形的外接圆性质是解题的关键．
7、A
【解析】
【分析】
直接根据点与圆的位置关系进行解答即可．
【详解】
解：∵⊙O的半径为5cm，点P与圆心O的距离为4cm，5cm＞4cm，
∴点P在圆内．
故选：A．
【点睛】
本题考查了点与圆的位置关系，当点到圆心的距离小于半径的长时，点在圆内；当点到圆心的距离等于半径的长时，点在圆上；当点到圆心的距离大于半径的长时，点在圆外．
8、B
【解析】
【分析】
连接OD，求出BC是⊙O的切线，根据切线长定理得出CD＝BC，根据切线的性质求出∠ODM＝90°，根据勾股定理求出MD，再根据勾股定理求出BC即可．
【详解】
解：连接OD，

∵MD切⊙O于D，
∴∠ODM＝90°，
∵⊙O的半径为2，MA＝AO，AB是⊙O的直径，
∴MO＝2+2＝4，MB＝4+2＝6，OD＝2，
由勾股定理得：MD＝＝＝2，
∵BC⊥AB，
∴BC切⊙O于B，
∵DC切⊙O于D，
∴CD＝BC，
设CD＝CB＝x，
在Rt△MBC中，由勾股定理得：MC2＝MB2+BC2，
即（2+x）2＝62+x2，
解得：x＝2，
即BC＝2，
故选：B．
【点睛】
本题考查了切线的性质和判定，圆周角定理，勾股定理等知识点，能综合运用定理进行推理是解此题的关键．
9、A
【解析】
【分析】
直接根据直线与圆的位置关系即可得出结论．
【详解】
解：∵⊙O的半径为6，直线m上有一动点P，OP=4，
∴直线与⊙O相交．
故选：A．
【点睛】
本题考查的是直线与圆的位置关系，熟知⊙O的半径为r，圆心O到直线l的距离为d，当d=r时，直线l和⊙O相切是解答此题的关键．
10、C
【解析】
【分析】
根据若直线上一点到圆心的距离等于圆的半径，则圆心到直线的距离等于或小于圆的半径，此时直线和圆相交或相切．
【详解】
解：∵半径为5的圆，直线l上一点到圆心的距离是5，
∴圆心到直线的距离等于或小于5，
∴直线和圆的位置关系为相交或相切，
故选：C．
【点睛】
本题考查了直线和圆的位置关系，判断的依据是半径和直线到圆心的距离的大小关系：设⊙O的半径为r，圆心O到直线l的距离为d，①直线l和⊙O相交⇔d＜r；②直线l和⊙O相切⇔d＝r；③直线l和⊙O相离⇔d＞r．
二、填空题
1、6
【解析】
【分析】
依题意，直角三角形性质，结合题意能够容纳的最大为内切圆，结合内切圆半径，利用等积法求解即可；
【详解】
设直角三角形中能容纳最大圆的半径为：；
依据直角三角形的性质：可得斜边长为：
依据直角三角形面积公式：，即为；
内切圆半径面积公式：，即为；
所以，可得：，所以直径为：；
故填：6；
【点睛】
本题主要考查直角三角形及其内切圆的性质，重点在理解题意和利用内切圆半径求解面积；
2、5
【解析】
【分析】
根据圆的确定方法做出过A，B，C三点的外接圆，从而得出答案．
【详解】
如图，分别作AB、BC的中垂线，两直线的交点为O，

以O为圆心、OA为半径作圆，则⊙O即为过A，B，C三点的外接圆，
由图可知，⊙O还经过点D、E、F、G、H这5个格点，
故答案为5．
【点睛】
此题考查了确定圆的方法，三角形的外接圆，解题的关键是根据题意确定三角形ABC外接圆的圆心．
3、30
【解析】
【分析】
连接OC，根据切线的性质定理得到∠OCD=90°，根据三角形内角和定理求出∠D．
【详解】
解：连接OC，

∵CD为⊙O的切线，
∴∠OCD=90°，
由圆周角定理得，∠COD=2∠A=60°，
∴∠D=90°-60°=30°，
故答案为：30．
【点睛】
本题考查的是切线的性质，圆周角定理，掌握圆的切线垂直于经过切点的半径是解题的关键．
4、3
【解析】
【分析】
由切线长定理和，可得为等边三角形，则．
【详解】
解：连接，如下图：

，分别为的切线，
，
为等腰三角形，
，
，
为等边三角形，
，
，
．
故答案为：3．
【点睛】
本题考查了等边三角形的判定和切线长定理，解题的关键是作出相应辅助线．
5、76
【解析】
【分析】
连接OA、OB，根据圆周角定理求得∠AOB，由切线的性质求出∠OAP=∠OBP=90°，再由四边形的内角和等于360°，即可得出答案
【详解】
解：连接OA、OB，，

∴∠AOB=104°
∵PA、PB是⊙O的两条切线，点A、B为切点，
∴∠OAP=∠OBP=90°
∵∠APB+∠OAP+∠AOB+∠OBP=360°
∴∠APB=180°-(∠OAP+∠AOB+∠OBP)=76°
故答案为：76
【点睛】
本题考查了切线的性质、四边形的内角和定理以及圆周角定理，利用切线性质和圆周角定理求出角的度数是解题的关键
三、解答题
1、 (1)见解析
(2)cm
【解析】
【分析】
（1）作∠ABC的平分线，交AC于点O，再以点O为圆心、OC为半径作圆；
（2）记⊙O与AB的切点为E，连接OE，则OC=OE，BC=BE，设OC=OE=r，则AO=AC-r，在Rt△AOE中，由AO2=AE2+OE2列出关于r的方程求解即可．
①设AC=3x，AB=5x，用勾股定理表示出BC的长，根据的周长为12cm，列方程求出x，从而可求出三边的长；
②设AC=3x，AB=5x，用勾股定理表示出BC的长，根据，列方程求出x，从而可求出三边的长；
(1)
解：如图，

(2)
解：如图，设与相切于点．连接OE，则OC=OE，BC=BE，设OC=OE=r，则AO=AC-r．
①∵，∴设AC=3x，AB=5x，
∴BC==4x，
∵的周长为12cm，
∴3x+4x+5x=12，
∴x=1，
∴AC=3，AB=5，
∵⊙O 与 AB 、 BC 所在直线相切
∴BE=BC=4，
∴AE=AB-BE=5-4=1，AO=3-r，
在Rt△AOE中，
∵AO2=AE2+OE2，
∴(3-r)2=12+r2，
∴r=；

②∵，∴设AC=3x，AB=5x，
∴BC==4x，
∵，
∴4x=12，
∴x=1，
∴AC=3，AB=5，
∵⊙O 与 AB 、 BC 所在直线相切
∴BE=BC=4，
∴AE=AB-BE=5-4=1，AO=3-r，
在Rt△AOE中，
∵AO2=AE2+OE2，
∴(3-r)2=12+r2，
∴r=；
即⊙O的半径为cm．
【点睛】
本题考查了作图—复杂作图，勾股定理，切线的性质，以及切线长定理，解题的关键是掌握角平分线的尺规作图和性质、切线的性质和切线长定理及勾股定理．
2、 (1)见解析
(2)
(3)①见解析；②
【解析】
【分析】
（1）根据正方形的性质以及动点的路程相等，证明，根据同角的余角相等，即可证明，即；
（2）当t＝0时，点M与点B重合，当时，点随之停止，求得运动轨迹为圆，根据弧长公式进行计算即可；
（3）①根据（2）可得△CME的外接圆的圆心O是斜边CE的中点，继而判断点D、C、M、E在同一个圆（）上；②当与AB相切时，与正方形的各边共有5个交点，如图5则有6个交点，所以“当与AB相切时”是临界情况．如图4，当与AB相切（切点为G），连接OG，并延长GO交CD于点H，在Rt△CHO中求得半径,进而勾股定理求得，即可求得当时，与正方形的各边共有6个交点．
(1)
四边形是正方形，
，
又的运动速度都是2cm/s，






即

(2)
∵．
∴点M在以CB为直径的圆上，如图1，当t＝0时，点M与点B重合；
如图2，当t＝3时，点M为正方形对角线的交点．点M的运动路径为圆，其路径长．
故答案为：
(3)
①如图3．由前面结论可知：
∴△CME的外接圆的圆心O是斜边CE的中点，
则
在Rt△CDE中，，O是CE的中点．
∴，
∴
∴点D、C、M、E在同一个圆（）上，
即点D在△CME的外接圆上；．
②．
如图4，当与AB相切时，与正方形的各边共有5个交点，如图5则有6个交点，所以“当与AB相切时”是临界情况．
如图4，当与AB相切（切点为G），连接OG，并延长GO交CD于点H．
∵AB与相切，
∴，
又∵，
∴，

设的半径为R．由题意得：
在Rt△CHO中，，解得
∴
∴，即
∴如图5，当时，与正方形的各边共有6个交点．

【点睛】
本题考查了求弧长，切线的性质，直径所对的圆周角是直角，三角形的外心，正方形的性质，全等三角形的性质与判定，分类讨论是解题的关键．
3、 (1)相切，理由见解析
(2)
【解析】
【分析】
（1）连接OD，根据角平分线的性质与角的等量代换易得∠ODE＝90°，而D是圆上的一点；故可得直线DE与⊙O相切；
（2）连接BD，根据勾股定理得到AD＝＝2，根据圆周角定理得到∠ADB＝90°，根据相似三角形的性质列方程得到AB＝5，即可求解．
(1)
解：所在直线与相切．
理由：连接．

∵，
∴．
∵平分，
∴．
∴．
∴．
∴．
∵，
∴．
∴．
∴．
∵是半径，
∴所在直线与相切．
(2)
解：连接．
∵是的直径，
∴．
∴．
又∵，
∴．
∴．
∵，，，
∴．
∴．
∴的半径为．
【点睛】
本题考查的是直线与圆的位置关系，相似三角形的判定和性质及勾股定理，正确的作出辅助线是解题的关键．
4、 (1)见解析
(2)的半径长为．
【解析】
【分析】
（1）根据切线的性质，可得，由平行线的性质，等边对等角，等量代换即可得，进而得证；
（2）连接，根据直径所对的圆周角是直角，勾股定理求得，证明列出比例式，代入数值求解可得，进而求得半径
(1)
证明：如图，连接，
∵是的切线，
∴，
∵，
∴，
∴，
∵，
∴，
∴，即平分；

(2)
解：如图，连接，
在中，，，
由勾股定理得：，
∵是的直径，
∴，
∴，
∵，
∴，
∴，即，
解得：，
∴的半径长为．

【点睛】
本题考查了切线的性质，直径所对的圆周角是直角，相似三角形的性质与判定，勾股定理，掌握圆的相关知识以及相似三角形的是解题的关键．
5、 (1)见解析
(2)
【解析】
【分析】
（1）连接，利用角平分线的定义和等腰三角形的性质可证，从而，得到，根据切线的判定方法可证是的切线；
（2）证明，利用相似三角形的性质可求的半径．
(1)
证明：连接，
∵，
∴，
∴是直径，是的中点．
∵平分，
∴，
∵，
∴，
∴，
∴．
又∵，
∴，
∴，
又∵经过半径的外端，
∴是的切线．

(2)
解：∵，
∴，
在与中，
，，
∴．
∴，
在中，，，
∴.
设半径为，则，，
即，
∴．
∴的半径为．
【点睛】
本题考查了切线的判定，等腰三角形的性质，平行线的判定与性质，以及相似三角形的判定与性质，掌握切线的判定方法是解（1）的关键，掌握相似三角形的判定与性质是解（2）的关键．