冀教版九年级下册第29章 直线与圆的位置关系综合与测试优秀一课一练

这是一份冀教版九年级下册第29章 直线与圆的位置关系综合与测试优秀一课一练，共34页。试卷主要包含了在平面直角坐标系中，以点，下列说法正确的是等内容，欢迎下载使用。

九年级数学下册第二十九章直线与圆的位置关系专题攻克
考试时间：90分钟；命题人：数学教研组
考生注意：
1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟
2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。
第I卷（选择题 30分）
一、单选题（10小题，每小题3分，共计30分）
1、如图所示，⊙O的半径为5，点O到直线l的距离为7，P是直线l上的一个动点，PQ与⊙O相切于点Q．则PQ的最小值为（ ）

A． B． C．2 D．2
2、如图，是的切线，B为切点，连接，与交于点C，D为上一动点（点D不与点C、点B重合），连接．若，则的度数为（ ）

A． B． C． D．
3、如图，在平面直角坐标系xOy中，点A（0，3），点B（2，1），点C（2，－3）．则经画图操作可知：△ABC的外接圆的圆心坐标是（ ）

A．（－2，－1） B．（－1，0） C．（－1，－1） D．（0，－1）
4、如图是一个含有3个正方形的相框，其中∠BCD＝∠DEF＝90°，AB＝2，CD＝3，EF＝5，将它镶嵌在一个圆形的金属框上，使A，G， H三点刚好在金属框上，则该金属框的半径是（ ）

A． B． C． D．
5、圆O的半径为5cm，点A到圆心O的距离OA＝4cm，则点A与圆O的位置关系为（　　）
A．点A在圆上 B．点A在圆内 C．点A在圆外 D．无法确定
6、在平面直角坐标系中，以点（2，3）为圆心，3为半径的圆，一定（ ）
A．与x轴相切，与y轴相切 B．与x轴相切，与y轴相交
C．与x轴相交，与y轴相切 D．与x轴相交，与y轴相交
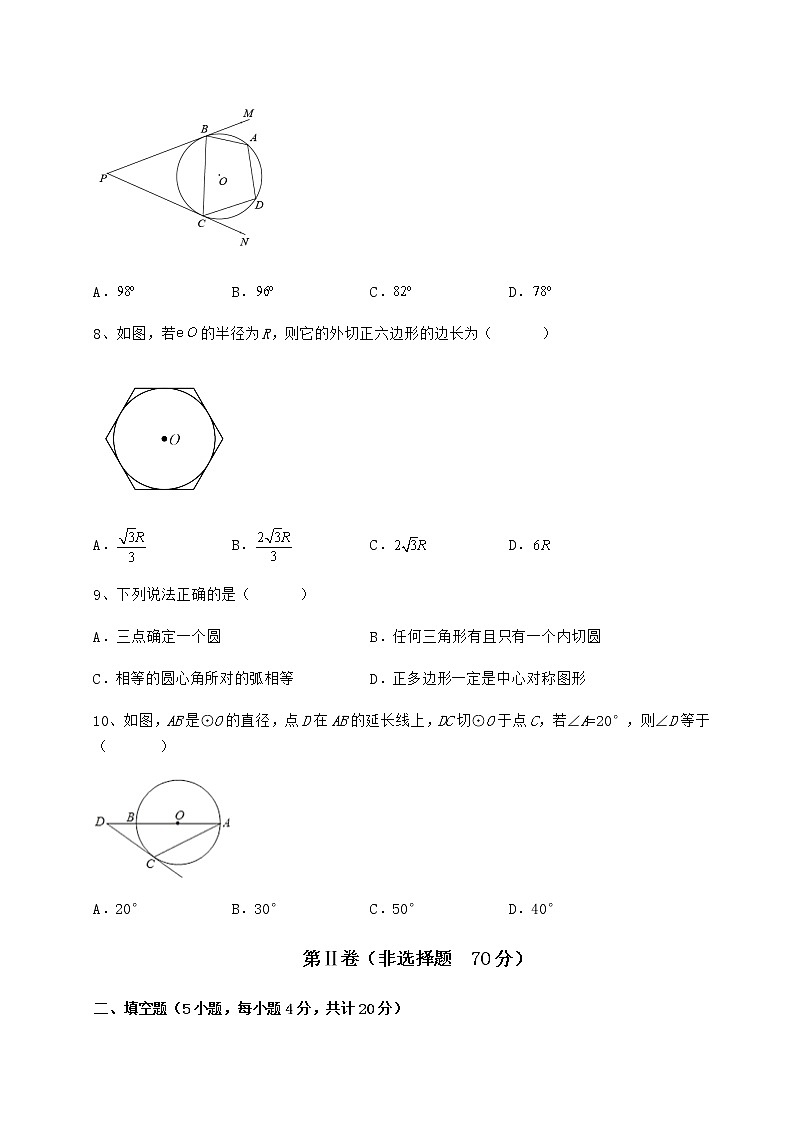
7、如图，，是的切线，，是切点，，是上的点，若，，则的度数为（ ）

A． B． C． D．
8、如图，若的半径为R，则它的外切正六边形的边长为（ ）

A． B． C． D．
9、下列说法正确的是（ ）
A．三点确定一个圆 B．任何三角形有且只有一个内切圆
C．相等的圆心角所对的弧相等 D．正多边形一定是中心对称图形
10、如图，AB是⊙O的直径，点D在AB的延长线上，DC切⊙O于点C，若∠A=20°，则∠D等于（ ）

A．20° B．30° C．50° D．40°
第Ⅱ卷（非选择题 70分）
二、填空题（5小题，每小题4分，共计20分）
1、在Rt△ABC中，∠ACB=90°，BC=3，AC=4，直线l经过△ABC的内心O，过点C作CD⊥l，垂足为D，连接AD，则AD的最小值是=____．

2、若的半径为5cm，点到圆心的距离为4cm，那么点与的位置关系是__．
3、已知的半径为5，点A到点O的距离为7，则点A在圆______．（填“内”或“上”或“外”）
4、如图，直线AB与x轴、y轴分别相交于A、B两点，点A（－3，0），点 B（0，），圆心P的坐标为（1，0），圆P与y轴相切与点O．若将圆P沿x轴向左移动，当圆P与该直线相交时，令圆心P的横坐标为m，则m的取值范围是________．

5、如图，⊙O的半径为5cm，正六边形ABCDEF内接于⊙O，则图中阴影部分的面积为 ___．

三、解答题（5小题，每小题10分，共计50分）
1、如图，中，．

(1)用直尺和圆规作，使圆心在边上，且与、所在直线相切（不写作法，保留作图痕迹）；
(2)在（1）的条件下，再从以下两个条件①“，的周长为12cm；②，”中选择一个作为条件，并求的半径．
2、如图，点在轴正半轴上，，点是第一象限内的一点，以为直径的圆交轴于，两点，，两点的横坐标是方程的两个根，，连接．

(1)如图（1），连接．
①求的正切值；
②求点的坐标．
(2)如图（2），若点是的中点，作于点，连接，，，求证：．
3、苏科版教材八年级下册第94页第19题，小明在学过圆之后，对该题进行重新探究，请你和他一起完成问题探究．
【问题探究】小明把原问题转化为动点问题，如图1，在边长为6cm的正方形ABCD中，点E从点A出发，沿边AD向点D运动，同时，点F从点B出发，沿边BA向点A运动，它们的运动速度都是2cm/s，当点E运动到点D时，两点同时停止运动，连接CF、BE交于点M，设点E， F运动时问为t秒．

(1)【问题提出】如图1，点E，F分别在方形ABCD中的边AD、AB上，且，连接BE、CF交于点M，求证：．请你先帮小明加以证明．
(2)如图1，在点E、F的运动过程中，点M也随之运动，请直接写出点M的运动路径长 cm．
(3)如图2，连接CE，在点E、F的运动过程中．
①试说明点D在△CME的外接圆O上；
②若①中的O与正方形的各边共有6个交点，请直接写出t的取值范围．
4、如图，在中，，平分，与交于点，，垂足为，与交于点，经过，，三点的与交于点．

(1)求证是的切线；
(2)若，，求的半径．
5、如图，PA，PB是圆的切线，A，B为切点．

(1)求作：这个圆的圆心O（用尺规作图，保留作图痕迹，不写作法和证明）；
(2)在（1）的条件下，延长AO交射线PB于C点，若AC＝4，PA＝3，请补全图形，并求⊙O的半径．

-参考答案-
一、单选题
1、C
【解析】
【分析】
由切线的性质可知OQ⊥PQ，在Rt△OPQ中，OQ=5，则可知当OP最小时，PQ有最小值，当OP⊥l时，OP最小，利用勾股定理可求得PQ的最小值．
【详解】
∵PQ与⊙O相切于点Q，
∴OQ⊥PQ，
∴PQ2=OP2-OQ2=OP2-52=OP2-25，
∴当OP最小时，PQ有最小值，
∵点O到直线l的距离为7，
∴OP的最小值为7，
∴PQ的最小值=，
故选：C．
【点睛】
本题主要考查切线的性质，掌握过切点的半径与切线垂直是解题的关键．
2、B
【解析】
【分析】
如图：连接OB，由切线的性质可得∠OBA=90°，再根据直角三角形两锐角互余求得∠COB，然后再根据圆周角定理解答即可．
【详解】
解：如图：连接OB，

∵是的切线，B为切点
∴∠OBA=90°
∵
∴∠COB=90°-42°=48°
∴=∠COB=24°．
故选B．
【点睛】
本题主要考查了切线的性质、圆周角定理等知识点，掌握圆周角等于对应圆心角的一半成为解答本题的关键．
3、A
【解析】
【分析】
首先由△ABC的外心即是三角形三边垂直平分线的交点，所以在平面直角坐标系中作AB与BC的垂线，两垂线的交点即为△ABC的外心．
【详解】
解：∵△ABC的外心即是三角形三边垂直平分线的交点，
如图所示：EF与MN的交点O′即为所求的△ABC的外心，
∴△ABC的外心坐标是（﹣2，﹣1）．
故选：A

【点睛】
此题考查了三角形外心的知识．注意三角形的外心即是三角形三边垂直平分线的交点．解此题的关键是数形结合思想的应用．
4、A
【解析】
【分析】
如图，记过A，G， H三点的圆为则是，的垂直平分线的交点， 记的交点为 的交点为 延长交于为的垂直平分线，结合正方形的性质可得：再设利用勾股定理建立方程，再解方程即可得到答案.
【详解】
解：如图，记过A，G， H三点的圆为则是，的垂直平分线的交点，
记的交点为 的交点为 延长交于为的垂直平分线，结合正方形的性质可得：

四边形为正方形，则

设 而AB＝2，CD＝3，EF＝5，结合正方形的性质可得：

而


又 而


解得：

故选A
【点睛】
本题考查的是正方形的性质，三角形外接圆圆心的确定，圆的基本性质，勾股定理的应用，二次根式的化简，确定过A，G， H三点的圆的圆心是解本题的关键.
5、B
【解析】
【分析】
根据点与圆的位置关系的判定方法进行判断．
【详解】
解：∵⊙O的半径为5cm，点A到圆心O的距离为4cm，
即点A到圆心O的距离小于圆的半径，
∴点A在⊙O内．
故选：B．
【点睛】
本题考查了点与圆的位置关系：设⊙O的半径为r，点P到圆心的距离OP=d，则有点P在圆外⇔d＞r；点P在圆上⇔d=r；点P在圆内⇔d＜r．
6、B
【解析】
【分析】
由已知点(2,3)可求该点到x轴，y轴的距离，再与半径比较，确定圆与坐标轴的位置关系．设d为直线与圆的距离，r为圆的半径，则有若dr，则直线与圆相离．
【详解】
解：∵点(2,3)到x轴的距离是3，等于半径，
到y轴的距离是2，小于半径，
∴圆与y轴相交，与x轴相切．
故选B．
【点睛】
本题考查的是直线与圆的位置关系，解决此类问题可通过比较圆心到直线距离d与圆半径大小关系完成判定．
7、A
【解析】
【分析】
如图，连接先求解 再利用圆周角定理可得，从而可得答案.
【详解】
解：如图，连接
，是的切线，







故选A
【点睛】
本题考查的是三角形的内角和定理，四边形的内角和定理，圆周角定理的应用，圆的切线的性质的应用，理解是解本题的关键.
8、B
【解析】
【分析】
如图连结OA，OB，OG，根据六边形ABCDEF为圆外切正六边形，得出∠AOB=60°△AOB为等边三角形，根据点G为切点，可得OG⊥AB，可得OG平分∠AOB，得出∠AOC=，根据锐角三角函数求解即可．
【详解】
解：如图连结OA，OB，OG，
∵六边形ABCDEF为圆外切正六边形，
∴∠AOB=360°÷6=60°，△AOB为等边三角形，
∵点G为切点，
∴OG⊥AB，
∴OG平分∠AOB，
∴∠AOC=，
∴cos30°=，
∴．
故选择B．

【点睛】
本题考查圆与外切正六边形性质，等边三角形性质，锐角三角形函数，掌握圆与外切正六边形性质，等边三角形性质，锐角三角形函数是解题关键．
9、B
【解析】
【分析】
根据确定圆的条件、三角形的内切圆、圆心角化和弧的关系、中心对称图形的概念判断．
【详解】
解：A、不在同一直线上的三点确定一个圆，故错误；
B、任何三角形有且只有一个内切圆，正确；
C、在同圆或等圆中，相等的圆心角所对的弧相等，故错误；
D、边数是偶数的正多边形一定是中心对称图形，故错误；
故选：B．
【点睛】
本题考查的是命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题．判断命题的真假关键是要熟悉课本中的性质定理．
10、C
【解析】
【分析】
连接CO利用切线的性质定理得出∠OCD=90°，进而求出∠DOC=40°即可得出答案．
【详解】
解：连接OC，

∵DC切⊙O于点C，
∴∠OCD=90°，
∵∠A=20°，
∴∠OCA=20°，
∴∠DOC=40°，
∴∠D=90°-40°=50°．
故选：C．
【点睛】
本题主要考查了切线的性质以及三角形外角性质等知识，根据已知得出∠OCD=90°是解题关键．
二、填空题
1、
【解析】
【分析】
先利用切线长定理求得OC=，再判断出当点D运动到线段QA上时，AD取得最小值，
然后利用勾股定理求解即可．
【详解】
解：⊙O 与Rt△ABC三边的切点分别为E、F、G，连接OE、OF、OG、OC，

∵⊙O是Rt△ABC内切圆，∠ACB=90°，BC=3，AC=4，
∴CE=CF，BE=BG，AF=AG，则四边形OECF是正方形，AB==5，
设正方形OECF的边长为x，则BE=BG=3-x，AF=AG=4-x，
依题意得：3-x+4-x=5，
解得：x=1，
∴OC=，
∵CD⊥l，即∠CDO=90°，
∴点D在以OC为直径的⊙Q上，

连接QA，过点Q作QP⊥AC于点P，
当点D运动到线段QA上时，AD取得最小值，
∴CP=QP=，AP=AC-CP=，⊙Q的半径为QD=，
∴QA=，
∴AD的最小值为AQ-QD=，
故答案为：．
【点睛】
本题考查了内心的性质，切线长定理，圆周角定理，勾股定理，解答本题的关键是明确题意，找出所求问题需要的条件．
2、点在圆内
【解析】
【分析】
比较点到圆心的距离d与半径r的大小关系；当时，点在圆外；当时，点在圆上；当时，点在圆内；求值后进行判断即可．
【详解】
解：的半径为，点A到圆心的距离为

点A与的位置关系是：点A在圆内
故答案为：点A在圆内．
【点睛】
本题考查了点与圆的位置关系．解题的关键在于比较点到圆心的距离d与半径r的大小关系．
3、外
【解析】
【分析】
直接根据点与圆的位置关系的判定方法进行判断．
【详解】
解：∵⊙O的半径是5，点A到圆心O的距离是7，
即点A到圆心O的距离大于圆的半径，
∴点A在⊙O外．
故答案为：外．
【点睛】
本题考查了点与圆的位置关系：设⊙O的半径为r，点P到圆心的距离OP=d，则有点P在圆外⇔d＞r；点P在圆上⇔d=r；点P在圆内⇔d＜r．
4、
【解析】
【分析】
当⊙P在直线AB下方与直线AB相切时，可求得此时m的值；当⊙P在直线AB上方与直线AB相切时，可求得此时m的值，从而可确定符合题意的m的取值范围．
【详解】
∵圆心P的坐标为（1，0），⊙P与y轴相切与点O
∴⊙P的半径为1
∵点A（－3，0），点 B（0，）
∴OA=3，
∴
∴∠BAO=30°
当⊙P在直线AB下方与直线AB相切时，如图，设切点为C，连接PC

则PC⊥AB，且PC=1
∴AP=2PC=2
∴OP=OA−AP=3−2=1
∴P点坐标为(−1，0)
即m=−1
当⊙P在直线AB上方与直线AB相切时，如图，设切点为C，连接PD

则PD⊥AB，且PD=1
∴AP=2PD=2
∴OP=OA+AP=3+2=5
∴P点坐标为(−5，0)
即m=−5
∴⊙P沿x轴向左移动，当⊙P与直线AB相交时，m的取值范围为
故答案为：
【点睛】
本题考查了直线与圆相交的位置关系，切线的性质定理等知识，这里通过讨论直线与圆相切的情况来解决直线与圆相交的情况，体现了转化思想，注意相切有两种情况，不要出现遗漏的情况．
5、
【解析】
【分析】
根据图形分析可得求阴影部分面积实为求扇形面积，将原图阴影部分面积转化为扇形面积求解即可．
【详解】

如图，连接BO，OC，OA，
由题意得：△BOC，△AOB都是等边三角形，
∴∠AOB＝∠OBC＝60°，
∴OA∥BC，
∴，
．
故答案为：．
【点睛】
本题考查正多边形与圆、扇形的面积公式、平行线的性质等知识，解题的关键是得出．
三、解答题
1、 (1)见解析
(2)cm
【解析】
【分析】
（1）作∠ABC的平分线，交AC于点O，再以点O为圆心、OC为半径作圆；
（2）记⊙O与AB的切点为E，连接OE，则OC=OE，BC=BE，设OC=OE=r，则AO=AC-r，在Rt△AOE中，由AO2=AE2+OE2列出关于r的方程求解即可．
①设AC=3x，AB=5x，用勾股定理表示出BC的长，根据的周长为12cm，列方程求出x，从而可求出三边的长；
②设AC=3x，AB=5x，用勾股定理表示出BC的长，根据，列方程求出x，从而可求出三边的长；
(1)
解：如图，

(2)
解：如图，设与相切于点．连接OE，则OC=OE，BC=BE，设OC=OE=r，则AO=AC-r．
①∵，∴设AC=3x，AB=5x，
∴BC==4x，
∵的周长为12cm，
∴3x+4x+5x=12，
∴x=1，
∴AC=3，AB=5，
∵⊙O 与 AB 、 BC 所在直线相切
∴BE=BC=4，
∴AE=AB-BE=5-4=1，AO=3-r，
在Rt△AOE中，
∵AO2=AE2+OE2，
∴(3-r)2=12+r2，
∴r=；

②∵，∴设AC=3x，AB=5x，
∴BC==4x，
∵，
∴4x=12，
∴x=1，
∴AC=3，AB=5，
∵⊙O 与 AB 、 BC 所在直线相切
∴BE=BC=4，
∴AE=AB-BE=5-4=1，AO=3-r，
在Rt△AOE中，
∵AO2=AE2+OE2，
∴(3-r)2=12+r2，
∴r=；
即⊙O的半径为cm．
【点睛】
本题考查了作图—复杂作图，勾股定理，切线的性质，以及切线长定理，解题的关键是掌握角平分线的尺规作图和性质、切线的性质和切线长定理及勾股定理．
2、 (1)①，②（4，3）
(2)见解析
【解析】
【分析】
（1）①过点P作PH⊥DC于H，作AF⊥PH于F，连接PD、AD，利用因式分解法解出一元二次方程，求出OD、OC，根据垂径定理求出DH，根据勾股定理计算求出半径，根据圆周角定理得到∠ADB＝90°，根据正切的定义计算即可；②过点B作BE⊥x轴于点E，作AG⊥BE于G，根据平行线分线段成比例定理定理分别求出OE、BE，得到点B的坐标；
（2）过点E作EH⊥x轴于H，证明△EHD≌△EFB，得到EH＝EF，DH＝BF，再证明Rt△EHC≌Rt△EFC，得到CH＝CF，结合图形计算，证明结论．
(1)
解：①以AB为直径的圆的圆心为P，
过点P作PH⊥DC于H，作AF⊥PH于F，连接PD、AD，
则DH＝HC＝DC，四边形AOHF为矩形，
∴AF＝OH，FH＝OA＝1，
解方程x2﹣4x+3＝0，得x1＝1，x2＝3，
∵OC＞OD，
∴OD＝1，OC＝3，
∴DC＝2，
∴DH＝1，
∴AF＝OH＝2，
设圆的半径为r，则PH2＝，
∴PF＝PH﹣FH，
在Rt△APF中，AP2＝AF2+PF2，即r2＝22+（PH﹣1）2，
解得：r＝，PH＝2，PF＝PH﹣FH＝1，
∵∠AOD＝90°，OA＝OD＝1，
∴AD＝，
∵AB为直径，
∴∠ADB＝90°，
∴BD＝=＝3，
∴tan∠ABD＝＝＝；
②过点B作BE⊥x轴于点E，交圆于点G，连接AG，
∴∠BEO＝90°，
∵AB为直径，
∴∠AGB＝90°，
∵∠AOE＝90°，
∴四边形AOEG是矩形，
∴OE＝AG，OA＝EG＝1，
∵AF＝2，
∵PH⊥DC，
∴PH⊥AG，
∴AF＝FG＝2，
∴AG＝OE＝4，BG＝2PF＝2，
∴BE＝3，
∴点B的坐标为（4，3）；

(2)
证明：过点E作EH⊥x轴于H，
∵点E是的中点，
∴＝，
∴ED＝EB，
∵四边形EDCB为圆P的内接四边形，
∴∠EDH＝∠EBF，
在△EHD和△EFB中，
，
∴△EHD≌△EFB（AAS），
∴EH＝EF，DH＝BF，
在Rt△EHC和Rt△EFC中，
，
∴Rt△EHC≌Rt△EFC（HL），
∴CH＝CF，
∴2CF＝CH+CF＝CD+DH+BC﹣BF＝BC+CD．

【点睛】
本题考查的是圆周角定理、全等三角形的判定和性质、垂径定理、勾股定理的应用，正确作出辅助线、求出圆的半径是解题的关键．
3、 (1)见解析
(2)
(3)①见解析；②
【解析】
【分析】
（1）根据正方形的性质以及动点的路程相等，证明，根据同角的余角相等，即可证明，即；
（2）当t＝0时，点M与点B重合，当时，点随之停止，求得运动轨迹为圆，根据弧长公式进行计算即可；
（3）①根据（2）可得△CME的外接圆的圆心O是斜边CE的中点，继而判断点D、C、M、E在同一个圆（）上；②当与AB相切时，与正方形的各边共有5个交点，如图5则有6个交点，所以“当与AB相切时”是临界情况．如图4，当与AB相切（切点为G），连接OG，并延长GO交CD于点H，在Rt△CHO中求得半径,进而勾股定理求得，即可求得当时，与正方形的各边共有6个交点．
(1)
四边形是正方形，
，
又的运动速度都是2cm/s，






即

(2)
∵．
∴点M在以CB为直径的圆上，如图1，当t＝0时，点M与点B重合；
如图2，当t＝3时，点M为正方形对角线的交点．点M的运动路径为圆，其路径长．
故答案为：
(3)
①如图3．由前面结论可知：
∴△CME的外接圆的圆心O是斜边CE的中点，
则
在Rt△CDE中，，O是CE的中点．
∴，
∴
∴点D、C、M、E在同一个圆（）上，
即点D在△CME的外接圆上；．
②．
如图4，当与AB相切时，与正方形的各边共有5个交点，如图5则有6个交点，所以“当与AB相切时”是临界情况．
如图4，当与AB相切（切点为G），连接OG，并延长GO交CD于点H．
∵AB与相切，
∴，
又∵，
∴，

设的半径为R．由题意得：
在Rt△CHO中，，解得
∴
∴，即
∴如图5，当时，与正方形的各边共有6个交点．

【点睛】
本题考查了求弧长，切线的性质，直径所对的圆周角是直角，三角形的外心，正方形的性质，全等三角形的性质与判定，分类讨论是解题的关键．
4、 (1)见解析
(2)
【解析】
【分析】
（1）连接，利用角平分线的定义和等腰三角形的性质可证，从而，得到，根据切线的判定方法可证是的切线；
（2）证明，利用相似三角形的性质可求的半径．
(1)
证明：连接，
∵，
∴，
∴是直径，是的中点．
∵平分，
∴，
∵，
∴，
∴，
∴．
又∵，
∴，
∴，
又∵经过半径的外端，
∴是的切线．

(2)
解：∵，
∴，
在与中，
，，
∴．
∴，
在中，，，
∴.
设半径为，则，，
即，
∴．
∴的半径为．
【点睛】
本题考查了切线的判定，等腰三角形的性质，平行线的判定与性质，以及相似三角形的判定与性质，掌握切线的判定方法是解（1）的关键，掌握相似三角形的判定与性质是解（2）的关键．
5、 (1)见解析；
(2)见解析，的半径为
【解析】
【分析】
（1）过点B作BP的垂线，作∠APB的平分线，二线的交点就是圆心；
（2）根据切线的性质，利用勾股定理，建立一元一次方程求解即可．
(1)
如图所示，点O即为所求

(2)
如图，∵PA是圆的切线，AO是半径，PB是圆的切线，
∴∠CAP=90°，PA=PB=3，∠CBO=90°，
∵AC=4，
∴PC==5，BC=5-3=2，
设圆的半径为x，则OC=4-x，
∴，
解得x=，
故圆的半径为．
【点睛】
本题考查了垂线的画法，角的平分线的画法，切线的性质，切线长定理，勾股定理，一元一次方程的解法，熟练掌握切线的性质，切线长定理和勾股定理是解题的关键．