初中数学冀教版八年级下册第二十二章 四边形综合与测试精品复习练习题

这是一份初中数学冀教版八年级下册第二十二章 四边形综合与测试精品复习练习题，共34页。
八年级数学下册第二十二章四边形定向测试
考试时间：90分钟；命题人：数学教研组
考生注意：
1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟
2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。
第I卷（选择题 30分）
一、单选题（10小题，每小题3分，共计30分）
1、如图．在长方形纸片ABCD中，AB=12，AD=20，所示，折叠纸片，使点A落在BC边上的A′处，折痕为PQ，当点A′在BC边上移动时，折痕的端点P、Q也随之移动．点P，Q分别在边AB、AD上移动，则点A′在BC边上可移动的最大距离为（ ）

A．8 B．10 C．12 D．16
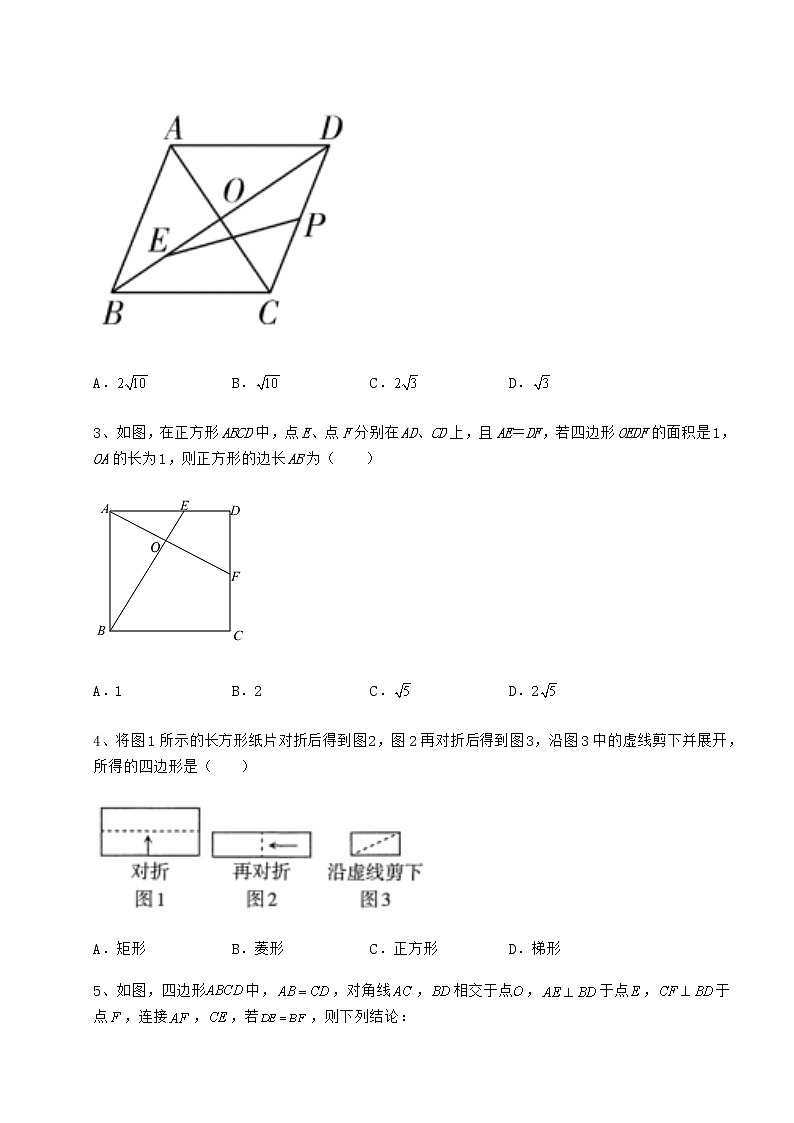
2、如图，菱形ABCD的对角线AC和BD相交于点O，，，E是OB的中点，P是CD的中点，连接PE，则线段PE的长为（ ）

A． B． C． D．
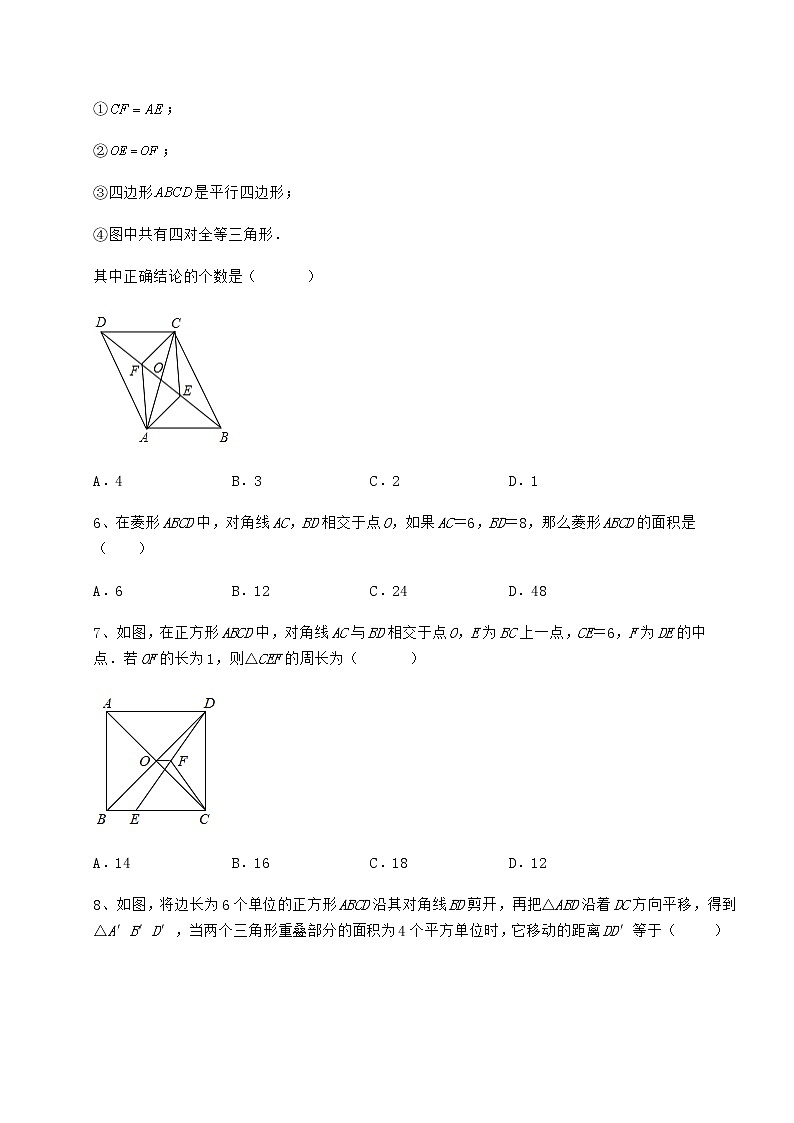
3、如图，在正方形ABCD中，点E、点F分别在AD、CD上，且AE＝DF，若四边形OEDF的面积是1，OA的长为1，则正方形的边长AB为（　　）

A．1 B．2 C． D．2
4、将图1所示的长方形纸片对折后得到图2，图2再对折后得到图3，沿图3中的虚线剪下并展开，所得的四边形是（　　）

A．矩形 B．菱形 C．正方形 D．梯形
5、如图，四边形中，，对角线，相交于点，于点，于点，连接，，若，则下列结论：
①；
②；
③四边形是平行四边形；
④图中共有四对全等三角形．
其中正确结论的个数是（ ）

A．4 B．3 C．2 D．1
6、在菱形ABCD中，对角线AC，BD相交于点O，如果AC＝6，BD＝8，那么菱形ABCD的面积是（　　）
A．6 B．12 C．24 D．48
7、如图，在正方形ABCD中，对角线AC与BD相交于点O，E为BC上一点，CE＝6，F为DE的中点．若OF的长为1，则△CEF的周长为（ ）

A．14 B．16 C．18 D．12
8、如图，将边长为6个单位的正方形ABCD沿其对角线BD剪开，再把△ABD沿着DC方向平移，得到△A′B′D′，当两个三角形重叠部分的面积为4个平方单位时，它移动的距离DD′等于（ ）

A．2 B． C． D．
9、若一个正多边形的每个内角度数都为108°，则这个正多边形的边数是 (　　)
A．5 B．6 C．8 D．10
10、一多边形的每一个内角都等于它相邻外角的4倍，则该多边形的内角和是（　　）
A．360° B．900° C．1440° D．1800°
第Ⅱ卷（非选择题 70分）
二、填空题（5小题，每小题4分，共计20分）
1、将矩形纸片ABCD（AB＜BC）沿过点B的直线折叠，使点A落在BC边上的点F处，折痕为BE（如图1）；再沿过点E的直线折叠，使点D落在BE上的点D'处，折痕为EG（如图2）：再展开纸片（如图3），则图3中∠FEG的大小是__．

2、如图，点M，N分别是的边AB，AC的中点，若，，则______．

3、如图，在平行四边形中，是对角线，，点是的中点，平分，于点，连接．已知，，则的长为_______．

4、已知一个多边形的内角和为，则这个多边形是________边形．
5、如图，在平面直角坐标系xOy中，有一边长为1的正方形OABC，点B在x轴的正半轴上，如果以对角线OB为边作第二个正方形OBB1C1，再以对角线OB1为边作第三个正方形OB1B2C2，…，照此规律作下去，则B2的坐标是 ___；B2020的坐标是 ___．

三、解答题（5小题，每小题10分，共计50分）
1、背景资料：在已知所在平面上求一点P，使它到三角形的三个顶点的距离之和最小.这个问题是法国数学家费马1640年前后向意大利物理学家托里拆利提出的，所求的点被人们称为“费马点”．如图1，当三个内角均小于120°时，费马点P在内部，当时，则取得最小值．

(1)如图2，等边内有一点P，若点P到顶点A、B、C的距离分别为3，4，5，求的度数，为了解决本题，我们可以将绕顶点A旋转到处，此时这样就可以利用旋转变换，将三条线段、、转化到一个三角形中，从而求出_______；
知识生成：怎样找三个内角均小于120°的三角形的费马点呢？为此我们只要以三角形一边在外侧作等边三角形并连接等边三角形的顶点与的另一顶点，则连线通过三角形内部的费马点．请同学们探索以下问题．
(2)如图3，三个内角均小于120°，在外侧作等边三角形，连接，求证：过的费马点．
(3)如图4，在中，，，，点P为的费马点，连接、、，求的值．
(4)如图5，在正方形中，点E为内部任意一点，连接、、，且边长；求的最小值．
2、（1）【探究一】如图1，我们可以用不同的算法来计算图形的面积．

①方法1：如果把图1看成一个大正方形，那么它的面积为 ；
②方法2：如果把图1看成是由2个大小不同的正方形和2个大小相同的小长方形组成的图形，那么它的面积为 ；（写成关于a、b的两次三项式）用两种不同的算法计算同一个图形的面积，可以得到等式 ．
（2）【探究二】如图2，从一个顶点处引n条射线，请你数一数共有多少个锐角呢?
①方法1：一路往下数，不回头数．
以OA1为边的锐角有∠A1OA2、∠A1OA3、∠A1OA4、…、∠A1OAn，共有（n－1）个；
以OA2为边的锐角有∠A2OA3、∠A2OA4、…、∠A2OAn，共有（n－2）个；
以OA3为边的锐角有∠A3OA4、…、∠A3OAn，共有（n－3）个；
以OAn－1为边的锐角有∠An－1OAn，共有1个；
则图中锐角的总个数是 ；
②方法2：每一条边都能和除它以外的（n－1）条边形成锐角，共有n条边，可形成n（n－1）个锐角，但所有锐角都数了两遍，所以锐角的总个数是 ；
用两种不同的方法数锐角个数，可以得到等式 ．
（3）【应用】分别利用【探究一】中得到的等式和【探究二】中运用的思想解决问题．
①计算：19782＋20222；
②多边形中连接任意两个不相邻顶点的线段叫做对角线，如五边形共有5条对角线，则十七边形共有 条对角线，n边形共有 条对角线．
3、如图，直线，线段分别与直线、交于点、点，满足．

(1)使用尺规完成基本作图：作线段的垂直平分线交于点，交于点，交线段于点，连接、、、．（保留作图痕迹，不写做法，不下结论）
(2)求证：四边形为菱形．（请补全下面的证明过程）
证明：
____①____
垂直平分
，
∴____②____
____③____



∴四边形是___④_____

∴四边形是菱形（______⑤__________）（填推理的依据）．
4、已知：线段m．
求作：矩形ABCD，使矩形宽AB＝m，对角线AC＝m．

5、【问题情境】如图1，在中，，垂足为D，我们可以得到如下正确结论：①；②；③，这些结论是由古希酷著名数学家欧几里得在《几何原本》最先提出的，我们称之为“射影定理”，又称“欧几里德定理”．
(1)请证明“射影定理”中的结论③．
(2)【结论运用】如图2，正方形的边长为6，点O是对角线、的交点，点E在上，过点C作，垂足为F，连接．

①求证：．
②若，求的长．

-参考答案-
一、单选题
1、A
【解析】
【分析】
根据翻折的性质，可得BA′与AP的关系，根据线段的和差，可得A′C，根据勾股定理，可得A′C，根据线段的和差，可得答案．
【详解】
解：①在长方形纸片ABCD中，AB=12，AD=20，
∴BC=AD=20，
当p与B重合时，BA′=BA=12，
CA′=BC-BA′=20-12=8，
②当Q与D重合时，
由折叠得A′D=AD=20，
由勾股定理，得
CA′==16，
CA′最远是16，CA′最近是8，点A′在BC边上可移动的最大距离为16-8=8，
故选：A．
【点睛】
本题考查了矩形的性质，翻折变换，利用了翻折的性质，勾股定理，分类讨论是解题关键．
2、A
【解析】
【分析】
取OD的中点H，连接HP，由菱形的性质可得AC⊥BD，AO＝CO＝4，OB＝OD＝6，由三角形中位线定理可得，，可得EH＝6，，由勾股定理可求PE的长．
【详解】
解：如图，取OD的中点H，连接HP

∵四边形ABCD是菱形
∴AC⊥BD，AO＝CO＝4，OB＝OD＝6
∵点H是OD中点，点E是OB的中点，点P是CD的中点
∴OH=3，OE=3，，
∴EH＝6，
在中，由勾股定理可得：
∴
故选：A
【点睛】
本题考查了菱形的性质，三角形中位线定理，勾股定理，添加恰当辅助线构造直角三角形是解题的关键．
3、C
【解析】
【分析】
根据正方形的性质得到AB=AD，∠BAE=∠ADF=90°，根据全等三角形的性质得到∠ABE=∠DAF，求得∠AOB=90°，根据三角形的面积公式得到OA=1，由勾股定理即可得到答案．
【详解】
解：∵四边形ABCD是正方形，
∴AB=AD，∠BAE=∠ADF=90°，
在△ABE与△DAF中，
，
∴△ABE≌△DAF（SAS），
∴∠ABE=∠DAF，
∴∠ABE+∠BAO=∠DAF+∠BAO=90°，
∴∠AOB=90°，
∵△ABE≌△DAF，
∴S△ABE=S△DAF，
∴S△ABE-S△AOE=S△DAF-S△AOE，
即S△ABO=S四边形OEDF=1，
∵OA=1，
∴BO=2，
∴AB=，
故选：C．
【点睛】
本题考查了正方形的性质，全等三角形的判定和性质，勾股定理，证得△ABE≌△DAF是解题的关键．
4、B
【解析】
【分析】
根据操作过程可还原展开后的纸片形状，并判断其属于什么图形．
【详解】

展得到的图形如上图，
由操作过程可知：AB=CD，BC=AD，
∴四边形ABCD是平行四边形，
∵AC⊥BD，
∴四边形ABCD为菱形，
故选：B．
【点睛】
本题考查平行四边形的判定，和菱形的判定，拥有良好的空间想象能力是解决本题的关键．
5、B
【解析】
【分析】
由DE=BF以及DF=BE，可证明Rt△DCF≌Rt△BAE，由FC=EA，以及双垂直可证，四边形CFAE是平行四边形由此可证明②③正确．
【详解】
解：，
，
在和中，
，
，
，（故①正确）；
于点，于点，
，
，
四边形是平行四边形，
，（故②正确）；
，
，
，
，
四边形是平行四边形，（故③正确）；
由以上可得出：，，，
，，，等．（故④错误），
故正确的有3个，
故选：．
【点评】
此题主要考查了平行四边形的性质与判定以及全等三角形的判定与性质等知识，得出是解题关键．
6、C
【解析】
【分析】
利用菱形的面积公式即可求解．
【详解】
解：菱形ABCD的面积＝＝＝24，
故选：C．
【点睛】
本题考查菱形的面积公式，菱形的面积等于对角线乘积的一半．
7、B
【解析】
【分析】
根据中位线的性质及直角三角形斜边上中线的性质可得：，结合图形得出的周长为，再由中位线的性质得出，在中，利用勾股定理确定，即可得出结论．
【详解】
解：在正方形ABCD中，，，，
∵F为DE的中点，O为BD的中点，
∴OF为的中位线且CF为斜边上的中线，
∴，
∴的周长为，
∵，
∴，
∵，
∴，
∴，
在中，，，，
∴，
∴的周长为，
故选：B．
【点睛】
题目主要考查正方形的性质，三角形中位线的性质，勾股定理，直角三角形斜边中线的性质等，理解题意，熟练掌握运用各个知识点是解题关键．
8、B
【解析】
【分析】
先判断重叠部分的形状，然后设DD'=x，进而表示D'C等相关的线段，最后通过重叠部分的面积列出方程求出x的值即可得到答案．
【详解】
解：∵四边形ABCD是正方形，
∴△ABD和△BCD是等腰直角三角形，
如图，记A'D'与BD的交点为点E，B'D'与BC的交点为F，

由平移的性质得，△DD'E和△D'CF为等腰直角三角形，
∴重叠部分的四边形D'EBF为平行四边形，
设DD'=x，则D'C=6-x，D'E=x，
∴S▱D'EBF=D'E•D'C=（6-x）x=4，
解得：x=3+或x=3-，
故选：B．
【点睛】
本题考查了正方形的性质、等腰直角三角形的性质、平移的性质，通过平移的性质得到重叠部分四边形的形状是解题的关键．
9、A
【解析】
【分析】
先求出多边形的每一个外角的度数，再利用多边形的外角和即可求出答案．
【详解】
解：∵多边形的每一个内角都等于108°，多边形的内角与外角互为邻补角，
∴每个外角是：180°−108°＝72°，
∴多边形中外角的个数是360°÷72°＝5，则多边形的边数是5．
故选：A．
【点睛】
本题主要考查了多边形的外角和定理，已知外角求边数的这种方法是需要熟练掌握的内容．
10、C
【解析】
【分析】
设每一个外角都为x，则相邻的内角为4x，然后根据“邻补角和为180°”列方程求得外角的大小，然后再根据多边形外角和定理求得多边形边数，最后运用多边形内角和公式求解即可．
【详解】
解：设每一个外角都为x，则相邻的内角为4x，
由题意得，4x+x＝180°，
解得：x＝36°，
多边形的外角和为360°，
360°÷36°＝10，
所以这个多边形的边数为10，
则该多边形的内角和是：（10﹣8）×180＝1440°．
故选：C．
【点睛】
本题主要考查了多边形内角和相邻外角的关系、多边形的外角和、多边形内角和等知识点，掌握多边形的外角和为360°是解答本题的关键．
二、填空题
1、22.5°
【解析】
【分析】
根据折叠的性质可知，∠A=∠EFB=90°，AB=BF，以及纸片ABCD为矩形可得，∠AEF为直角，进而可以判断四边形ABFE为正方形，进而通过∠AEB，∠BEG的角度计算出∠FEG的大小．
【详解】
解：由折叠可知△AEB≌△FEB，
∴∠A=∠EFB=90°，AB=BF，
∵纸片ABCD为矩形，
∴AE∥BF，
∴∠AEF=180°－∠BFE=90°，
∵AB=BF，∠A=∠AEF=∠EFB=90°，
∴四边形ABFE为正方形，
∴∠AEB=45°，
∴∠BED=180°－45°=135°，
∴∠BEG=135°÷2=67.5°，
∴∠FEG=67.5°－45°=22.5°．
【点睛】
本题考查折叠的性质，矩形的性质，正方形的判定与性质，以及平行的相关性质，能够将正方形与矩形的性质相结合是解决本题的关键．
2、45°##45度
【解析】
【分析】
根据三角形中位线定理得出，进而利用平行线的性质解答即可．
【详解】
解：、分别是的边、的中点，
，
，
，，
，
，
故答案是：．
【点睛】
本题考查三角形中位线定理，解题的关键是根据三角形中位线定理得出．
3、##3.5##
【解析】
【分析】
延长AB、CF交于点H，由“ASA”可证△AFH≌△AFC，可得AC=AH=12，HF=CF，由三角形中位线定理可求解．
【详解】
解：如图，延长、交于点，

四边形是平行四边形，，，
，
平分，，
在和中，
，
，
，，
，
点是的中点，，
∴EF是△CBH的中位线，
，
故答案为：．
【点睛】
本题考查了平行四边形的性质，全等三角形的判定和性质，勾股定理，三角形中位线等知识，添加恰当辅助线构造全等三角形是本题的关键．
4、八##8
【解析】
【分析】
n边形的内角和是（n-2）•180°，如果已知多边形的边数，就可以得到一个关于边数的方程，解方程就可以求出多边形的边数．
【详解】
解：根据n边形的内角和公式，得
（n-2）•180=1080，
解得n=8．
∴这个多边形的边数是8．
故答案为：八．
【点睛】
本题考查了多边形的内角与外角，熟记内角和公式和外角和定理并列出方程是解题的关键．根据多边形的内角和定理，求边数的问题就可以转化为解方程的问题来解决．
5、
【解析】
【分析】
根据已知条件和勾股定理求出OB2的长度即可求出B2的坐标，再根据题意和图形可看出每经过一次变化，正方形都逆时针旋转45°，正方形的边长都乘以所以可求出从B到B2020变化的坐标．
【详解】
解：∵四边形OABC是边长为1正方形，
∴
∴
∴B1的坐标是，
∴，
∴B2的坐标是
根据题意和图形可看出每经过一次变化，正方形逆时针旋转45°，其边长乘以，
∴B3的坐标是
∴B4的坐标是
∴旋转8次则OB旋转一周，
∵从B到B2020经过了2020次变化，2020÷8=252…4，
∴从B到B2020与B4都在x轴负半轴上，
∴点B2020的坐标是
【点睛】
本题主要考查了规律型-点的坐标，解决本题的关键是利用正方形的变化过程寻找点的变化规律．
三、解答题
1、 (1)150°；
(2)见详解；
(3)；
(4)．
【解析】
【分析】
（1）根据旋转性质得出≌，得出∠BAP=∠CAP′，∠APB=∠AP′C，AP=AP′=3，BP=CP′=4，根据△ABC为等边三角形，得出∠BAC=60°，可证△APP′为等边三角形，PP′=AP=3，∠AP′P=60°，根据勾股定理逆定理，得出△PP′C是直角三角形，∠PP′C=90°，可求∠AP′C=∠APP+∠PPC=60°+90°=150°即可；
（2）将△APB逆时针旋转60°，得到△AB′P′，连结PP′，根据△APB≌△AB′P′，AP=AP′，PB=PB′，AB=AB′，根据∠PAP′=∠BAB′=60°，△APP′和△ABB′均为等边三角形，得出PP′=AP，根据，根据两点之间线段最短得出点C，点P，点P′，点B′四点共线时，最小=CB′，点P在CB′上即可；
（3）将△APB逆时针旋转60°，得到△AP′B′，连结BB′，PP′，得出△APB≌△AP′B′，可证△APP′和△ABB′均为等边三角形，得出PP′=AP，BB′=AB，∠ABB′=60°，根据，可得点C，点P，点P′，点B′四点共线时，最小=CB′，利用30°直角三角形性质得出AB=2AC=2，根据勾股定理BC=，可求BB′=AB=2，根据∠CBB′=∠ABC+∠ABB′=30°+60°=90°，在Rt△CBB′中，B′C=即可；
（4）将△BCE逆时针旋转60°得到△CE′B′，连结EE′，BB′，过点B′作B′F⊥AB，交AB延长线于F，得出△BCE≌△CE′B′，BE=B′E′，CE=CE′，CB=CB′，可证△ECE′与△BCB′均为等边三角形，得出EE′=EC，BB′=BC，∠B′BC=60°，，得出点C，点E，点E′，点B′四点共线时，最小=AB′，根据四边形ABCD为正方形，得出AB=BC=2，∠ABC=90°，可求∠FBB′=180°-∠ABC-∠CBB′=180°-90°-60°=30°，根据30°直角三角形性质得出BF=，勾股定理BF=，可求AF=AB+BF=2+，再根据勾股定理AB′=即可．
(1)
解：连结PP′，
∵≌，
∴∠BAP=∠CAP′，∠APB=∠AP′C，AP=AP′=3，BP=CP′=4，
∵△ABC为等边三角形，
∴∠BAC=60°
∴∠PAP′=∠PAC+∠CAP′=∠PAC+∠BAP=60°，
∴△APP′为等边三角形，
,∴PP′=AP=3，∠AP′P=60°，
在△P′PC中，PC=5，
，
∴△PP′C是直角三角形，∠PP′C=90°，
∴∠AP′C=∠APP+∠PPC=60°+90°=150°，
∴∠APB=∠AP′C=150°，
故答案为150°；

(2)
证明：将△APB逆时针旋转60°，得到△AB′P′，连结PP′，
∵△APB≌△AB′P′，
∴AP=AP′，PB=PB′，AB=AB′，
∵∠PAP′=∠BAB′=60°，
∴△APP′和△ABB′均为等边三角形，
∴PP′=AP，
∵，
∴点C，点P，点P′，点B′四点共线时，最小=CB′，
∴点P在CB′上，
∴过的费马点．

(3)
解：将△APB逆时针旋转60°，得到△AP′B′，连结BB′，PP′，
∴△APB≌△AP′B′，
∴AP′=AP，AB′=AB，
∵∠PAP′=∠BAB′=60°，
∴△APP′和△ABB′均为等边三角形，
∴PP′=AP，BB′=AB，∠ABB′=60°，
∵
∴点C，点P，点P′，点B′四点共线时，最小=CB′，
∵，，，
∴AB=2AC=2，根据勾股定理BC=
∴BB′=AB=2，
∵∠CBB′=∠ABC+∠ABB′=30°+60°=90°，
∴在Rt△CBB′中，B′C=
∴最小=CB′=；

(4)
解：将△BCE逆时针旋转60°得到△CE′B′，连结EE′，BB′，过点B′作B′F⊥AB，交AB延长线于F，
∴△BCE≌△CE′B′，
∴BE=B′E′，CE=CE′，CB=CB′，
∵∠ECE′=∠BCB′=60°，
∴△ECE′与△BCB′均为等边三角形，
∴EE′=EC，BB′=BC，∠B′BC=60°，
∵，
∴点C，点E，点E′，点B′四点共线时，最小=AB′，
∵四边形ABCD为正方形，
∴AB=BC=2，∠ABC=90°，
∴∠FBB′=180°-∠ABC-∠CBB′=180°-90°-60°=30°，
∵B′F⊥AF，
∴BF=，BF=，
∴AF=AB+BF=2+，
∴AB′=，
∴最小=AB′=．

【点睛】
本题考查图形旋转性质，等边三角形判定与性质，勾股定理，直角三角形判定与性质，两点之间线段最短，四点共线，正方形性质，30°直角三角形性质，掌握图形旋转性质，等边三角形判定与性质，勾股定理，直角三角形判定与性质，两点之间线段最短，四点共线，正方形性质，30°直角三角形性质是解题关键．
2、（1）①；②；=；（2）①（n－1）＋（n－2）＋（n－3）＋……＋1；②；（n－1）＋（n－2）＋（n－3）＋……＋1=；（3）①8000968；②119，n(n-3)
【解析】
【分析】
（1）①根据边长为(a+b)的正方形面积公式求解即可；
②利用矩形和正方形的面积公式求解即可；
（2）①根据题中的数据求和即可；
②根据题意求解即可；
（3）①利用（1）的规律求解即可；
②根据n边形从一个顶点出发可引出（n-3）条对角线．从n个顶点出发引出（n-3）条，而每条重复一次，所以n边形对角线的总条数为n(n-3)（n≥3，且n为整数）可得答案．
【详解】
解：（1）①大正方形的面积为；
②由2个大小不同的正方形和2个大小相同的小长方形组成的图形的面积为；
可以得到等式：=；
故答案为：①；②；=；
（2）①图中锐角的总个数是：（n－1）＋（n－2）＋（n－3）＋……＋1；
②锐角的总个数是n（n－1）；
可以得到等式为（n－1）＋（n－2）＋（n－3）＋……＋1=n（n－1）；
故答案为：①（n－1）＋（n－2）＋（n－3）＋……＋1；②n（n－1）；（n－1）＋（n－2）＋（n－3）＋……＋1=n（n－1）；
（3）①19782＋20222＝[2000＋（－22）]2＋（2000＋22）2
＝20002＋（－22）2＋2×2000×（－22）＋20002＋222＋2×2000×22
＝2×（20002＋222）
＝2×[4000000＋（20＋2）2]
＝2×[4000000＋（202＋22＋2×20×2）]＝8000968；
②一个四边形共有2条对角线，即×4×(4-3)=2；
一个五边形共有5条对角线，即×5×(5-3)=5；
一个六边形共有9条对角线，即×6×(6-3)=9；
……，
一个十七边形共有×17×(17-3)=119条对角线；
一个n边形共有n(n-3)（n≥3，且n为整数）条对角线．
故答案为：119，n(n-3)．
【点睛】
本题考查了图形的变化规律，完全平方公式，多边形的对角线，对于这种图形的变化规律的问题，读懂题目信息，找到变化规律是解题的关键．
3、 (1)见解析
(2)①；②；③；④平行四边形；⑤对角线互相垂直的平行四边形是菱形
【解析】
【分析】
（1）分别以A、D为圆心，大于AD的一半长为半径，画弧，两弧交于两点，然后过这两点作直线交l1于E，交l2于F，直线EF为线段AD的垂直平分线，连接、、、即可；
（2）：根据，内错角相等得出∠2①，根据垂直平分 ，得出，，可证②△EOC，根据全等三角形性质得出OF③，再证，根据对角线互相平分的四边形是平行四边形判定四边形是平行四边形④，根据对角线互相垂直即可得出四边形是菱形（对角线互相垂直的平行四边形是菱形⑤）．
(1)
解：分别以A、D为圆心，大于AD的一半长为半径，画弧，两弧交于两点，然后过这两点作直线交l1于E，交l2于F，直线EF为线段AD的垂直平分线，连接、、、即可；
如图所示

(2)
证明：，
∠2①，
垂直平分 ，
，，
∴②△EOC，
OF③，
，
，
，
∴四边形是平行四边形④，
，
∴四边形是菱形（对角线互相垂直的平行四边形是菱形⑤），
故答案为：①；②；③；④平行四边形；⑤对角线互相垂直的平行四边形是菱形．
【点睛】
本题考查尺规作图，垂直平分线性质，三角形全等判定与性质，菱形的判定，掌握尺规作图，垂直平分线性质，三角形全等判定与性质，菱形的判定是解题关键．
4、见详解
【解析】
【分析】
先作m的垂直平分线，取m的一半为AB，然后以点A为圆心，以m长为半径画弧，交m的垂直平分线于C，连结AC，利用作一个角等于已知角，过A作BC的平行线AD，过C作AB的平行线CD，两线交于D即可．
【详解】
解：先作m的垂直平分线，取m的一半为AB，
以点A为圆心，以m长为半径画弧，交m的垂直平分线于C，连结AC，
过A作BC的平行线，与过C作AB的平行线交于D，
则四边形ABCD为所求作矩形；

∵AD∥BC，CD∥AB，
∴四边形ABCD为平行四边形，
∵BC⊥AB，
∴∠ABC=90°，
∴四边形ABCD为矩形，
∵AB=，AC=m，
∴矩形的宽与对角线满足条件，
∴四边形ABCD为所求作矩形．
【点睛】
本题考查矩形作图，线段垂直平分线，作线段等于已知线段，平行线作法，掌握矩形作图，线段垂直平分线，作线段等于已知线段，平行线作法是解题关键．
5、 (1)见解析；
(2)①见解析；②．
【解析】
【分析】
（1）由AA证明，再由相似三角形对应边称比例得到，继而解题；
（2）①由“射影定理”分别解得，，整理出，再结合即可证明；
②由勾股定理解得，再根据得到，代入数值解题即可．
(1)
证明：







(2)
①四边形ABCD是正方形









②在中，


在，



．
【点睛】
本题考查相似三角形的综合题，涉及勾股定理、正方形等知识，是重要考点，掌握相关知识是解题关键．