数学八年级下册第二十二章 四边形综合与测试精品课后练习题

这是一份数学八年级下册第二十二章 四边形综合与测试精品课后练习题，共28页。试卷主要包含了下列命题错误的是等内容，欢迎下载使用。
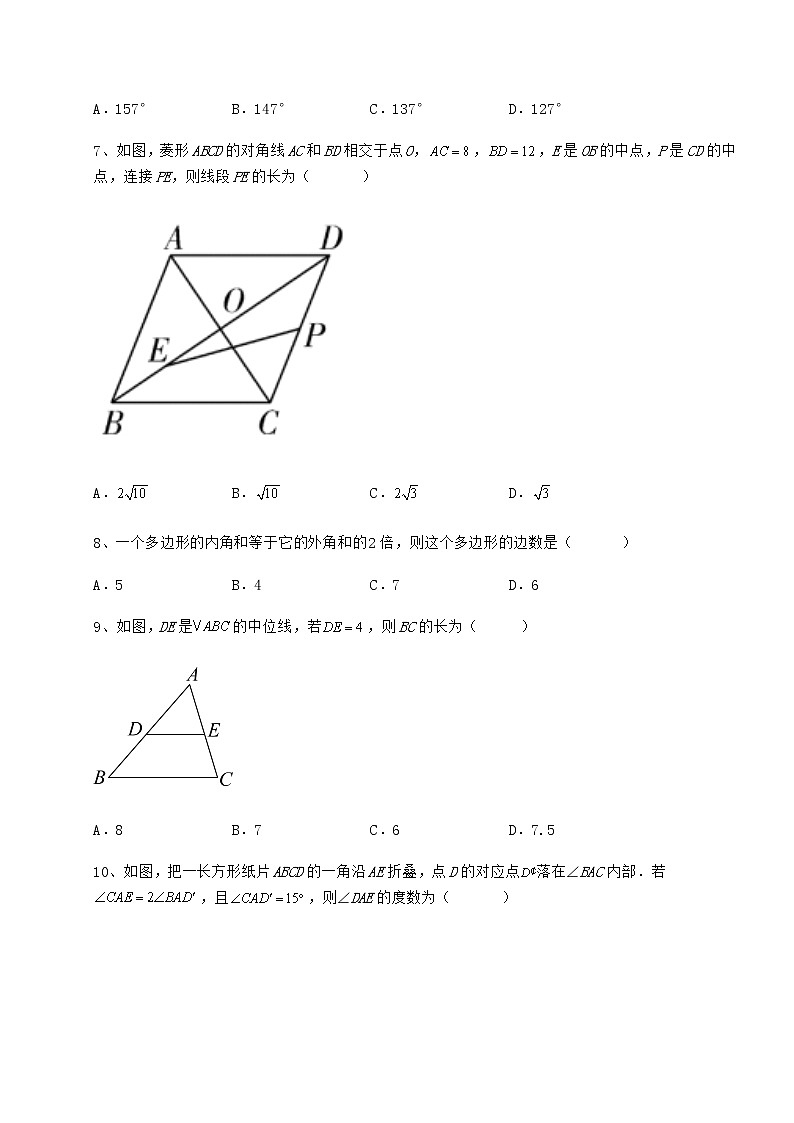
八年级数学下册第二十二章四边形专项测试 考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。第I卷（选择题  30分）一、单选题（10小题，每小题3分，共计30分）1、如图，五边形中，，CP，DP分别平分，，则（　　　）A．60° B．72° C．70° D．78°2、如图，为了测量一块不规则绿地B，C两点间的距离，可以在绿地的一侧选定一点A，然后测量出AB，AC的中点D，E，如果测量出D，E两点间的距离是8m，那么绿地B，C两点间的距离是（　　）A．4m B．8m C．16m D．20m3、若n边形每个内角都为156°，那么n等于（       ）A．8 B．12 C．15 D．164、下列命题错误的是（       ）A．两组对边分别平行的四边形是平行四边形B．两组对边分别相等的四边形是平行四边形C．一组对边平行，另一组对边相等的四边形是平行四边形D．对角线互相平分的四边形是平行四边形5、如图，四边形中，，对角线，相交于点，于点，于点，连接，，若，则下列结论：①；②；③四边形是平行四边形；④图中共有四对全等三角形．其中正确结论的个数是（       ）A．4 B．3 C．2 D．16、如图，四边形ABCD是平行四边形，对角线AC与BD交于点O，若，，则的度数为（       ）A．157° B．147° C．137° D．127°7、如图，菱形ABCD的对角线AC和BD相交于点O，，，E是OB的中点，P是CD的中点，连接PE，则线段PE的长为（       ）A． B． C． D．8、一个多边形的内角和等于它的外角和的2倍，则这个多边形的边数是（       ）A．5 B．4 C．7 D．69、如图，DE是的中位线，若，则BC的长为（　　　）A．8 B．7 C．6 D．7.510、如图，把一长方形纸片ABCD的一角沿AE折叠，点D的对应点落在∠BAC内部．若，且，则∠DAE的度数为（       ）A．12° B．24° C．39° D．45°第Ⅱ卷（非选择题  70分）二、填空题（5小题，每小题4分，共计20分）1、如图所示，是长方形地面，长，宽，中间竖有一堵砖墙高．一只蚂蚱从点爬到点，它必须翻过中间那堵墙，则它至少要走______的路程．2、如图，在中，，，射线AF是的平分线，交BC于点D，过点B作AB的垂线与射线AF交于点E，连结CE，M是DE的中点，连结BM并延长与AC的延长线交于点G．则下列结论正确的是______．①       ②BG垂直平分DE       ③       ④             ⑤3、如图，矩形ABCD中，AC，BD交于点O，M，N分别为BC，OC的中点．若MN＝4，则AC的长为__________．4、如图，在平行四边形ABCD中，对角线AC，BD交于点O，AC⊥AB，AB＝，且AC：BD＝2：3，那么AC的长为___．5、如图，矩形的两条对角线相交于点，已知，，则矩形对角线的长为_______．三、解答题（5小题，每小题10分，共计50分）1、如图，将△ABC放在每个小正方形的边长为1的网格中，点A，点B，点C均落在格点上．（1）计算AC2+BC2的值等于_____；（2）请在如图所示的网格中，用无刻度的直尺，画出一个以AB为一边的矩形，使该矩形的面积等于AC2+BC2，并简要说明画图方法（不要求证明）_____．2、如图，正方形ABCD中，E为BD上一点，AE的延长线交BC的延长线于点F，交CD于点H，G为FH的中点．(1)求证：AE=CE；(2)猜想线段AE，EG和GF之间的数量关系，并证明．3、如图，在矩形ABCD中，(1)尺规作图（不写作法，保留作图痕迹）：作对角线BD的垂直平分线EF分别交AD、BC于E、F点，交BD于O点．(2)在（1）的条件下，求证：AE=CF．4、（1）【发现证明】如图1，在正方形中，点，分别是，边上的动点，且，求证：．小明发现，当把绕点顺时针旋转90°至，使与重合时能够证明，请你给出证明过程．（2）【类比引申】①如图2，在正方形中，如果点，分别是，延长线上的动点，且，则（1）中的结论还成立吗？若不成立，请写出，，之间的数量关系______（不要求证明）②如图3，如果点，分别是，延长线上的动点，且，则，，之间的数量关系是______（不要求证明）（3）【联想拓展】如图1，若正方形的边长为6，，求的长．5、如图，矩形ABCD的对角线AC、BD相交于点O，AB＝5cm，∠BOC＝120°，求矩形对角线的长． -参考答案-一、单选题1、C【解析】【分析】根据五边形的内角和等于，由，可求的度数，再根据角平分线的定义可得与的角度和，进一步求得的度数．【详解】解：五边形的内角和等于，，，、的平分线在五边形内相交于点，，．故选：C．【点睛】本题主要考查了多边形的内角和公式，角平分线的定义，解题的关键是熟记公式，注意整体思想的运用．2、C【解析】【分析】根据三角形中位线定理即可求出．【详解】解：中，、分别是、的中点，为三角形的中位线，，，故选：C．【点睛】本题考查的是三角形中位线定理的应用，解题的关键是掌握三角形的中位线等于第三边的一半．3、C【解析】【分析】首先求得外角的度数，然后利用多边形的外角和是360度，列式计算即可求解．【详解】解：由题意可知：n边形每个外角的度数是：180°-156°=24°，则n=360°÷24°=15．故选：C．【点睛】本题考查了多边形的外角与内角，熟记多边形的外角和定理是关键．4、C【解析】【分析】根据平行四边形的判定逐项分析即可得．【详解】解：A、两组对边分别平行的四边形是平行四边形，正确，则此项不符合题意；B、两组对边分别相等的四边形是平行四边形，正确，则此项不符合题意；C、一组对边平行，另一组对边相等的四边形可能是平行四边形，也可能是等腰梯形，故原命题错误，此项符合题意；D、对角线互相平分的四边形是平行四边形，正确，则此项不符合题意，故选：C．【点睛】本题考查了平行四边形的判定，熟记平行四边形的判定是解题关键．5、B【解析】【分析】由DE=BF以及DF=BE，可证明Rt△DCF≌Rt△BAE，由FC=EA，以及双垂直可证，四边形CFAE是平行四边形由此可证明②③正确．【详解】解：，，在和中，，，，（故①正确）；于点，于点，，，四边形是平行四边形，，（故②正确）；，，，，四边形是平行四边形，（故③正确）；由以上可得出：，，，，，，等．（故④错误），故正确的有3个，故选：．【点评】此题主要考查了平行四边形的性质与判定以及全等三角形的判定与性质等知识，得出是解题关键．6、C【解析】【分析】根据平行四边形的性质推出AO=AB，求出∠AOB的度数，即可得到的度数．【详解】解：∵四边形ABCD是平行四边形，∴AC=2AO，∵，∴AO=AB，∵，∴，∴=，故选：C．【点睛】此题考查了平行四边形的性质，三角形的内角和，利用邻补角求角度，正确掌握平行四边形的性质是解题的关键．7、A【解析】【分析】取OD的中点H，连接HP，由菱形的性质可得AC⊥BD，AO＝CO＝4，OB＝OD＝6，由三角形中位线定理可得，，可得EH＝6，，由勾股定理可求PE的长．【详解】解：如图，取OD的中点H，连接HP∵四边形ABCD是菱形∴AC⊥BD，AO＝CO＝4，OB＝OD＝6∵点H是OD中点，点E是OB的中点，点P是CD的中点∴OH=3，OE=3，，∴EH＝6，在中，由勾股定理可得：∴故选：A【点睛】本题考查了菱形的性质，三角形中位线定理，勾股定理，添加恰当辅助线构造直角三角形是解题的关键．8、D【解析】【分析】利用多边形内角和公式和外角和定理，列出方程即可解决问题．【详解】解：根据题意，得：（n-2）×180=360×2，解得n=6．故选：D．【点睛】本题考查了多边形内角与外角，解答本题的关键是根据多边形内角和公式和外角和定理，利用方程法求边数．9、A【解析】【分析】已知DE是的中位线，，根据中位线定理即可求得BC的长．【详解】是的中位线，，，故选：A．【点睛】此题主要考查三角形中位线定理：三角形的中位线平行于第三边，并且等于第三边的一半；掌握中位线定理是解题的关键．10、C【解析】【分析】由折叠的性质得到，由长方形的性质得到，根据角的和差倍分得到，整理得 ，最后根据解题．【详解】解：折叠，是矩形故选：C．【点睛】本题考查角的计算、折叠性质、数形结合思想等知识，是重要考点，掌握相关知识是解题关键．二、填空题1、【解析】【分析】根据题意，将长方形底面和中间墙展开为平面图，并连接BD，根据两点之间直线段最短和勾股定理的性质计算，即可得到答案．【详解】将长方形底面和中间墙展开后的平面图如下，并连接BD根据题意，展开平面图中的∴一只蚂蚱从点爬到点，最短路径长度为展开平面图中BD长度∵是长方形地面∴ ∴ 故答案为：．【点睛】本题考查了立体图形展开图、矩形、两点之间直线段最短、勾股定理的知识；解题的关键是熟练掌握立体图形展开图、勾股定理的知识，从而完成求解．2、①②⑤【解析】【分析】先由题意得到∠ABE=∠ACB=∠BCG=90°，∠BAC=45°，再由角平分线的性质得到∠BAE=∠DAC=22.5°，从而推出∠BEA=∠ADC，则∠BDE=∠BED，再由三线合一定理即可证明BM⊥DE，∠GBE=∠DBG，即可判断②；得到∠MAG+∠MGA=90°，再由∠CBG+∠CGB=90°，可得∠DAC=∠GBC=22.5°，则∠GBE=22.5°，2∠GBE=45°，从而可证明△ACD≌△BCG，即可判断①；则CD=CG，再由AC=BC=BD+CD，可得到AC=BE+CG，即可判断⑤；由∠G=180°-∠BCG-∠CBG=67.5°，即可判断④；延长BE交AC延长线于G，先证△ABH是等腰直角三角形，得到C为AH的中点，然后证BE≠HE，即E不是BH的中点，得到CE不是△ABH的中位线，则CE与AB不平行，即可判断③．【详解】解：∵∠ACB=90°，BE⊥AB，AC=BC，∴∠ABE=∠ACB=∠BCG=90°，∠BAC=45°，∴∠BAE+∠BEA=90°，∠DAC+∠ADC=90°，∵AF平分∠BAC，∴∠BAE=∠DAC=22.5°，∴∠BEA=∠ADC，又∵∠ADC=∠BDE，∴∠BDE=∠BED，∴BD=ED，又∵M是DE的中点，∴BM⊥DE，∠GBE=∠DBG，∴BG垂直平分DE，∠AMG=90°，故②正确，∴∠MAG+∠MGA=90°，∵∠CBG+∠CGB=90°，∴∠DAC=∠GBC=22.5°，∴∠GBE=22.5°，∴2∠GBE=45°，又∵AC=BC，∴△ACD≌△BCG（ASA），故①正确；∴CD=CG，∵AC=BC=BD+CD，∴AC=BE+CG，故⑤正确；∵∠G=180°-∠BCG-∠CBG=67.5°，∴∠G≠2∠GBE，故④错误；如图所示，延长BE交AC延长线于G，∵∠ABH=∠ABC+∠CBH=90°，∠BAC=45°，∴△ABH是等腰直角三角形，∵BC⊥AH，∴C为AH的中点，∵AB≠AH，AF是∠BAH的角平分线，∴BE≠HE，即E不是BH的中点，∴CE不是△ABH的中位线，∴CE与AB不平行，∴BE与CE不垂直，故③错误；故答案为：①②⑤．【点睛】本题主要考查了全等三角形的性质与判定，等腰三角形的性质与判定，三角形中位线定理，三角形内角和定理，熟知等腰三角形的性质与判定条件是解题的挂件．3、16【解析】略4、4【解析】【分析】四边形是平行四边形，可得，由，可知，由可知在中勾股定理求解的值，进而求解的值．【详解】解：∵四边形是平行四边形∴∵∴∵∴∴设则解得：则故故答案为：4．【点睛】本题考查了勾股定理，平行四边形的性质等知识．解题的关键在于正确的求解．5、5【解析】【分析】由矩形的性质可证△AOB为等边三角形，可求BO=AB的长，即可求BD的长．【详解】解：∵四边形ABCD是矩形，∴AO=CO=BO=DO，∵∠AOD=120°，∴∠AOB=60°，且AO=BO，∴△ABO为等边三角形，∴AO=BO=AB=2.5，∴BD=5，故答案为：5．【点睛】本题考查矩形的性质，熟练掌握矩形的性质是本题的关键，①矩形的对边平行且相等；②矩形的四个角都是直角；③矩形的对角线相等且互相平分．三、解答题1、     11     见解析【解析】【分析】（1）直接利用勾股定理求出即可；（2）首先分别以AC、BC、AB为一边作正方形ACED，正方形BCNM，正方形ABHF；进而得出答案．【详解】解：（1）AC2+BC2＝（）2+32＝11；故答案为：11；（2）分别以AC、BC、AB为一边作正方形ACED，正方形BCNM，正方形ABHF；延长DE交MN于点Q，连接QC，平移QC至AG，BP位置，直线GP分别交AF，BH于点T，S，则四边形ABST即为所求，如图，【点睛】本题考查了勾股定理，无刻度直尺作图，平行四边形与矩形的性质，掌握勾股定理以及特殊四边形的性质是解题的关键．2、 (1)见解析(2)AE2+ GF2=EG2，证明见解析【解析】【分析】（1）根据“SAS”证明△ADE≌△CDE即可；（2）连接CG，可得CG=GF=GH=FH，再证明∠ECG=90°，然后在Rt△CEG中，可得CE2+CG2=EG2，进而可得线段AE，EG和GF之间的数量关系．(1)证明：∵四边形ABCD是正方形，∴AD=CD，∠ADE=∠CDE， 在△ADE和△CDE中，∴△ADE≌△CDE，∴AE=CE；(2)AE2+ GF2=EG2，理由：连接CG∵△ADE≌△CDE，∴∠1=∠2．∵G为FH的中点，∴CG=GF=GH=FH，∴∠6=∠7．∵∠5=∠6，∴∠5=∠7．∵∠1+∠5=90°，∴∠2+∠7=90°，即∠ECG=90°，在Rt△CEG中，CE2+CG2=EG2，∴AE2+ GF2=EG2．【点睛】本题考查了正方形的性质，全等三角形的判定与性质，直角三角形的性质，以及勾股定理等知识，证明△ADE≌△CDE是解（1）的关键，证明∠ECG=90°是解（2）的关键．3、 (1)见解析(2)见解析【解析】【分析】（1）利用尺规作出图形即可．（2）利用全等三角形的性质证明即可．(1)解：如图，直线EF即为所求作．．(2)证明：在矩形ABCD中，AD=BC，∠ADB=∠DBC，∵EF为BD的垂直平分线，∴∠EOD=∠FOB=90°，OB=OD，在△EOD与△FOB中，，∴△EOD≌△FOB（ASA），∴ED=BF，∴AD-ED=BC-BF，即AE=CF．【点睛】本题考查了作图-复杂作图，线段的垂直平分线，全等三角形的判定和性质等知识，解题的关键是理解题意，灵活运用所学知识解决问题．4、（1）见解析；（2）①不成立，结论：；②，见解析；（3）【解析】【分析】（1）证明，可得出，则结论得证；（2）①将绕点顺时针旋转至根据可证明，可得，则结论得证；②将绕点逆时针旋转至，证明，可得出，则结论得证；（3）求出，设，则，，在中，得出关于的方程，解出则可得解．【详解】（1）证明：把绕点顺时针旋转至，如图1，，，，，，，三点共线，，，，，，，，；（2）①不成立，结论：；证明：如图2，将绕点顺时针旋转至，，，，，，，，；②如图3，将绕点逆时针旋转至，，，，，，，，，．即．故答案为：．（3）解：由（1）可知，正方形的边长为6，，．，，设，则，，在中，，，解得：．，．【点睛】本题属于四边形综合题，主要考查了正方形的性质、旋转的性质、全等三角形的判定与性质以及勾股定理的综合应用，解题的关键是作辅助线构造全等三角形，根据全等三角形的对应边相等进行推导．5、10cm【解析】【分析】根据矩形性质得出∠ABC＝90°，AC＝BD，OA＝OC＝AC，OB＝OD＝BD，推出OA＝OB，求出等边三角形AOB，求出OA＝OB＝AB＝5，即可得出答案．【详解】解：∵∠BOC＝120°，∴∠AOB＝180°﹣120°＝60°，∵四边形ABCD是矩形，∴∠ABC＝90°，AC＝BD，OA＝OC＝AC，OB＝OD＝BD，∴OA＝OB，∵∠AOB＝60°，∴△AOB是等边三角形，∵AB＝5cm，∴OA＝OB＝AB＝5cm，∴AC＝2AO＝10cm，BD＝AC＝10cm．【点睛】本题考查了矩形的性质和等边三角形的性质和判定的应用，解此题的关键是求出OA、OB的长，题目比较典型，是一道比较好的题目．