冀教版八年级下册第二十二章 四边形综合与测试精品课堂检测

这是一份冀教版八年级下册第二十二章 四边形综合与测试精品课堂检测，共28页。试卷主要包含了已知等内容，欢迎下载使用。
八年级数学下册第二十二章四边形章节测试
考试时间：90分钟；命题人：数学教研组
考生注意：
1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟
2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。
第I卷（选择题 30分）
一、单选题（10小题，每小题3分，共计30分）
1、将图1所示的长方形纸片对折后得到图2，图2再对折后得到图3，沿图3中的虚线剪下并展开，所得的四边形是（　　）

A．矩形 B．菱形 C．正方形 D．梯形
2、能够判断一个四边形是矩形的条件是（ ）
A．对角线相等 B．对角线垂直
C．对角线互相平分且相等 D．对角线垂直且相等
3、已知锐角∠AOB，如图．

（1）在射线OA上取一点C，以点O为圆心，OC长为半径画弧，交射线OB于点D，连接CD；
（2）分别以点C，D为圆心，CD长为半径作弧，两弧交于点P，连接CP，DP；
（3）作射线OP交CD于点Q．
根据以上作图过程及所作图形，下列结论中错误的是（　　　）
A．四边形OCPD是菱形 B．CP=2QC
C．∠AOP=∠BOP D．CD⊥OP
4、如图，在▱ABCD中，点E在边BC上，连接AE，EM⊥AE，垂足为E，交CD于点M．AF⊥BC，垂足为F．BH⊥AE，垂足为H，交AF于点N，连接AC、NE.若AE=BN，AN=CE，则下列结论中正确的有（ ）个．

①；②是等腰直角三角形；③是等腰直角三角形；④；⑤．
A．1 B．3 C．4 D．5
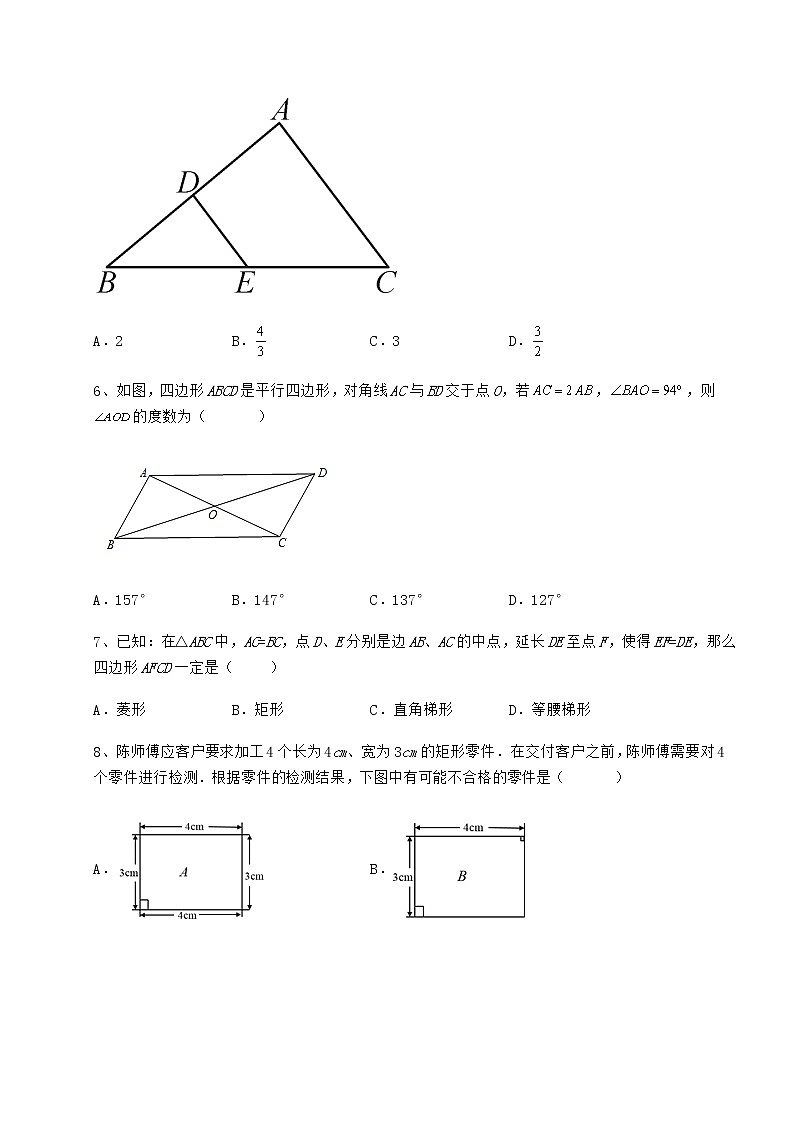
5、如图，点D，E分别是△ABC边BA，BC的中点，AC＝3，则DE的长为（ ）

A．2 B． C．3 D．
6、如图，四边形ABCD是平行四边形，对角线AC与BD交于点O，若，，则的度数为（ ）

A．157° B．147° C．137° D．127°
7、已知：在△ABC中，AC=BC，点D、E分别是边AB、AC的中点，延长DE至点F，使得EF=DE，那么四边形AFCD一定是（ ）
A．菱形 B．矩形 C．直角梯形 D．等腰梯形
8、陈师傅应客户要求加工4个长为4cm、宽为3cm的矩形零件．在交付客户之前，陈师傅需要对4个零件进行检测．根据零件的检测结果，下图中有可能不合格的零件是（ ）
A． B．
C． D．
9、如图，菱形OABC的边OA在平面直角坐标系中的x轴上，，，则点C的坐标为（ ）

A． B． C． D．
10、如图，平行四边形ABCD，∠BCD=120°，AB=2，BC=4，点E是直线BC上的点，点F是直线CD上的点，连接AF，AE，EF，点M，N分别是AF，EF的中点．连接MN，则MN的最小值为（ ）

A．1 B． C． D．
第Ⅱ卷（非选择题 70分）
二、填空题（5小题，每小题4分，共计20分）
1、四边形ABCD中，AD∥BC，要使它平行四边形，需要增加条件________（只需填一个 条件即可）．
2、如图，在平行四边形ABCD中，对角线AC，BD交于点O，AC⊥AB，AB＝，且AC：BD＝2：3，那么AC的长为___．

3、平行四边形的性质：平行四边形的两组对边分别________；平行四边形的两组对角分别________；平行四边形的对角线________．
4、如图所示，是长方形地面，长，宽，中间竖有一堵砖墙高．一只蚂蚱从点爬到点，它必须翻过中间那堵墙，则它至少要走______的路程．

5、如图，在矩形ABCD中，DE⊥CE，AE＜BE，AD＝4，AB＝10，则DE长为________．

三、解答题（5小题，每小题10分，共计50分）
1、如图，直线，线段分别与直线、交于点、点，满足．

(1)使用尺规完成基本作图：作线段的垂直平分线交于点，交于点，交线段于点，连接、、、．（保留作图痕迹，不写做法，不下结论）
(2)求证：四边形为菱形．（请补全下面的证明过程）
证明：
____①____
垂直平分
，
∴____②____
____③____



∴四边形是___④_____

∴四边形是菱形（______⑤__________）（填推理的依据）．
2、如图，已知矩形ABCD（AB＜AD）．E是BC上的点，AE=AD．

(1)在线段CD上作一点F，连接EF，使得∠EFC＝∠BEA(请用直尺和圆规作图，保留作图痕迹)；
(2)在（1）作出的图形中，若AB＝4，AD＝5，求DF的值．
3、如图，在菱形ABCD中，点E、F分别是边CD、BC的中点

(1)求证：四边形BDEG是平行四边形；
(2)若菱形ABCD的边长为13，对角线AC＝24，求EG的长．
4、如图，在四边形ABCD中，AB＝AD，AD//BC

(1)在图中，用尺规作线段BD的垂直平分线EF，分别交BD、BC于点E、F．（保留作图痕迹，不写作法）
(2)连接DF，证明四边形ABFD为菱形．
5、已知：在平行四边形ABCD中，分别延长BA，DC到点E，H，使得BE＝2AB，DH＝2CD．连接EH，分别交AD，BC于点F，G．

(1)求证：AF＝CG；
(2)连接BD交EH于点O，若EH⊥BD，则当线段AB与线段AD满足什么数量关系时，四边形BEDH是正方形？

-参考答案-
一、单选题
1、B
【解析】
【分析】
根据操作过程可还原展开后的纸片形状，并判断其属于什么图形．
【详解】

展得到的图形如上图，
由操作过程可知：AB=CD，BC=AD，
∴四边形ABCD是平行四边形，
∵AC⊥BD，
∴四边形ABCD为菱形，
故选：B．
【点睛】
本题考查平行四边形的判定，和菱形的判定，拥有良好的空间想象能力是解决本题的关键．
2、C
【解析】
略
3、A
【解析】
【分析】
根据作图信息可以判断出OP平分，由此可以逐一判断即可．
【详解】
解：由作图可知，平分
∴OP垂直平分线段CD
∴∠AOP=∠BOP，CD⊥OP
故选项C，D正确；
由作图可知，
∴是等边三角形，
∴
∵OP垂直平分线段CD
∴
∴CP=2QC
故选项B正确，不符合题意；
由作图可知，,不能确定四边形OCPD是菱形，故选项A符合题意，
故选：A
【点睛】
本题考查了基本作图，解题的关键是熟练掌握作图的依据．
4、C
【解析】
【分析】
证出∠NBF=∠EAF=∠MEC，再证明△NBF≌△EAF（AAS），得出BF=AF，NF=EF，证明△ANB≌△CEA得出∠CAE=∠ABN，推出∠ABF=∠FAC=45°；再证明△ANE≌△ECM得出CM=NE，由NF=NE=MC，得出AF=MC+EC，即可得出结论．
【详解】
解：∵BH⊥AE，AF⊥BC，AE⊥EM，
∴∠AEB+∠NBF=∠AEB+∠EAF=∠AEB+∠MEC=90°，
∴∠NBF=∠EAF=∠MEC，
在△NBF和△EAF中，，
∴△NBF≌△EAF（AAS）；
∴BF=AF，NF=EF，
∴∠ABC=45°，∠ENF=45°，
∴△NFE是等腰直角三角形，故③正确；
∵∠ANB=90°+∠EAF，∠CEA=90°+∠MEC，
∴∠ANB=∠CEA，
在△ANB和△CEA中，，
∴△ANB≌△CEA（SAS），故①正确；
∵AN=CE，NF=EF，
∴BF=AF=FC，
又∵AF⊥BC，∠ABC=45°，
∴△ABC是等腰直角三角形，故②正确；
在▱ABCD中，CD∥AB，且△ABC、△NFE都是等腰直角三角形，
∴∠ACD=∠BAC=90°，∠ACB=∠FNE=45°，
∴∠ANE=∠BCD=135°，
在△ANE和△ECM中，，
∴△ANE≌△ECM（ASA），故④正确；
∴CM=NE，
又∵NF=NE=MC，
∴AF=MC+EC，
∴AD=BC=2AF=MC+2EC，故⑤错误．
综上，①②③④正确，共4个，
故选：C．
【点睛】
本题考查了平行四边形的性质、全等三角形的判定与性质、等腰直角三角形的判定和性质等知识；熟练掌握平行四边形的性质，证明三角形全等是解题的关键．
5、D
【解析】
略
6、C
【解析】
【分析】
根据平行四边形的性质推出AO=AB，求出∠AOB的度数，即可得到的度数．
【详解】
解：∵四边形ABCD是平行四边形，
∴AC=2AO，
∵，
∴AO=AB，
∵，
∴，
∴=，
故选：C．
【点睛】
此题考查了平行四边形的性质，三角形的内角和，利用邻补角求角度，正确掌握平行四边形的性质是解题的关键．
7、B
【解析】
【分析】
先证明四边形ADCF是平行四边形，再证明AC=DF即可．
【详解】
解：∵E是AC中点，
∴AE=EC，
∵DE=EF，
∴四边形ADCF是平行四边形，
∵AD=DB，AE=EC，
∴DE=BC，
∴DF=BC，
∵CA=CB，
∴AC=DF，
∴四边形ADCF是矩形；
故选：B．

【点睛】
本题考查了矩形的判定、等腰三角形的性质、平行四边形的判定、三角形中位线定理；熟记对角线相等的平行四边形是矩形是解决问题的关键．
8、C
【解析】
【分析】
根据矩形的判定定理判断即可．
【详解】
∵A满足的条件是有一个角是直角的平行四边形是矩形，
∴A合格，不符合题意；
∵B满足的条件是三个角是直角的四边形是矩形，
∴B合格，不符合题意；
∵C满足的条件是有一个角是直角的四边形，
∴无法判定，C不合格，符合题意；
∵D满足的条件是有一个角是直角的平行四边形是矩形，
∴D合格，不符合题意；
故选C．
【点睛】
本题考查了矩形的判定定理，正确理解题意，熟练掌握矩形的判定定理是解题的关键．
9、A
【解析】
【分析】
如图：过C作CE⊥OA，垂足为E，然后求得∠OCE=30°，再根据含30°角直角三角形的性质求得OE，最后运用勾股定理求得CE即可解答.
【详解】
解：如图：过C作CE⊥OA，垂足为E，
∵菱形OABC，
∴OC=OA=4
∵，
∴∠OCE=30°
∵OC=4
∴OE=2
∴CE=
∴点C的坐标为.
故选A.

【点睛】
本题主要考查了菱形的性质、含30°直角三角形的性质、勾股定理等知识点，作出辅助线、求出OE、CE的长度是解答本题的关键.
10、C
【解析】
【分析】
先证明NM为△AEF的中位线，根据中位线性质得出MN=，可得AE最小时，MN最小，根据点E在直线BC上，根据点到直线的距离最短得出AE⊥BC时AE最短，根据在平行四边形ABCD中，∠BCD=120°，求出∠ABC=180°-∠BCD=180°-120°=60°，利用三角形内角和∠BAE=180°-∠ABE-∠AEB=180°-60°-90°=30°，利用30°直角三角形性质得出BE=，再利用勾股定理求出AE即可．
【详解】
解：∵M为FA中点，N为FE中点，
∴NM为△AEF的中位线，
∴MN=
∴AE最小时，MN最小，
∵点E在直线BC上，
根据点A到直线BC的距离最短，
∴AE⊥BC时AE最短，
∵在平行四边形ABCD中，∠BCD=120°，
∴∠ABC+∠BCD=180°，
∴∠ABC=180°-∠BCD=180°-120°=60°，
∴∠BAE=180°-∠ABE-∠AEB=180°-60°-90°=30°，
在Rt△ABE中，∠BAE=30°，AB=2，
∴BE=，
根据勾股定理AE最小值=,
∴MN=．
故选择C．
【点睛】
本题考查三角形中位线性质，平行四边形性质，点到直线距离，三角形内角和，30°直角三角形性质，勾股定理，掌握三角形中位线性质，平行四边形性质，点到直线距离，三角形内角和，30°直角三角形性质，勾股定理是解题关键．
二、填空题
1、AD=BC
【解析】
略
2、4
【解析】
【分析】
四边形是平行四边形，可得，由，可知，由可知在中勾股定理求解的值，进而求解的值．
【详解】
解：∵四边形是平行四边形
∴
∵
∴
∵
∴
∴设
则
解得：
则
故
故答案为：4．
【点睛】
本题考查了勾股定理，平行四边形的性质等知识．解题的关键在于正确的求解．
3、 相等 相等 互相平分
【解析】
略
4、
【解析】
【分析】
根据题意，将长方形底面和中间墙展开为平面图，并连接BD，根据两点之间直线段最短和勾股定理的性质计算，即可得到答案．
【详解】
将长方形底面和中间墙展开后的平面图如下，并连接BD

根据题意，展开平面图中的
∴一只蚂蚱从点爬到点，最短路径长度为展开平面图中BD长度
∵是长方形地面
∴
∴
故答案为：．
【点睛】
本题考查了立体图形展开图、矩形、两点之间直线段最短、勾股定理的知识；解题的关键是熟练掌握立体图形展开图、勾股定理的知识，从而完成求解．
5、
【解析】
【分析】
设AE＝x，则BE＝10﹣x，由勾股定理得AD2＋AE2＝DE2，BC2＋BE2＝CE2，DE2＋CE2＝CD2，则AD2＋AE2＋BC2＋BE2＝CD2，即42＋x2＋42＋（10﹣x）2＝102，解得：x＝2或x＝8（舍去），则AE＝2，然后由勾股定理即可求解．
【详解】
解：设AE＝x，则BE＝10﹣x，
∵四边形ABCD是矩形，
∴CD＝AB＝10，∠A＝∠B＝90°，
∴AD2＋AE2＝DE2，BC2＋BE2＝CE2，
∵DE⊥CE，
∴∠DEC＝90°，
∴DE2＋CE2＝CD2，
∴AD2＋AE2＋BC2＋BE2＝CD2，
即42＋x2＋42＋（10﹣x）2＝102，
解得：x＝2或x＝8（不合题意，舍去），
∴AE＝2，
∴DE＝＝＝2，
故答案为：2．
【点睛】
本题考查了矩形的性质，勾股定理，掌握勾股定理是解题的关键．
三、解答题
1、 (1)见解析
(2)①；②；③；④平行四边形；⑤对角线互相垂直的平行四边形是菱形
【解析】
【分析】
（1）分别以A、D为圆心，大于AD的一半长为半径，画弧，两弧交于两点，然后过这两点作直线交l1于E，交l2于F，直线EF为线段AD的垂直平分线，连接、、、即可；
（2）：根据，内错角相等得出∠2①，根据垂直平分 ，得出，，可证②△EOC，根据全等三角形性质得出OF③，再证，根据对角线互相平分的四边形是平行四边形判定四边形是平行四边形④，根据对角线互相垂直即可得出四边形是菱形（对角线互相垂直的平行四边形是菱形⑤）．
(1)
解：分别以A、D为圆心，大于AD的一半长为半径，画弧，两弧交于两点，然后过这两点作直线交l1于E，交l2于F，直线EF为线段AD的垂直平分线，连接、、、即可；
如图所示

(2)
证明：，
∠2①，
垂直平分 ，
，，
∴②△EOC，
OF③，
，
，
，
∴四边形是平行四边形④，
，
∴四边形是菱形（对角线互相垂直的平行四边形是菱形⑤），
故答案为：①；②；③；④平行四边形；⑤对角线互相垂直的平行四边形是菱形．
【点睛】
本题考查尺规作图，垂直平分线性质，三角形全等判定与性质，菱形的判定，掌握尺规作图，垂直平分线性质，三角形全等判定与性质，菱形的判定是解题关键．
2、 (1)见解析
(2)
【解析】
【分析】
（1）作∠DAE的角平分线，与DC的交点即为所求，理由：可先证明△AEF≌△ADF，可得∠AEF=∠D=90°，从而得到∠DAE+∠DFE=180°，进而得到∠EFC=∠DAE，再由AD∥BC，即可求解；
（2）根据矩形的性质可得∠B＝∠C＝∠D＝90°，AD＝BC＝5，AB＝CD＝4，从而得到BE＝3，进而得到EC＝2，然后在 中，由勾股定理，即可求解．
(1)
解：如图，作∠DAE的角平分线，与DC的交点即为所求．

∵AE=AD，∠EAF=∠DAF，AF=AF，
∴△AEF≌△ADF，
∴∠AEF=∠D=90°，
∴∠DAE+∠DFE=180°，
∵∠EFC+∠DFE=180°，
∴∠EFC=∠DAE，
∵在矩形ABCD中，AD∥BC，
∴∠BEA=∠DAE，
∴∠EFC＝∠BEA；
(2)
解：∵四边形ABCD是矩形，
∴∠B＝∠C＝∠D＝90°，AD＝BC＝5，AB＝CD＝4，
∵AE＝AD＝5，
∴BE＝＝＝3，
∴EC＝BC﹣BE＝5﹣3＝2，
由（1）得：△AEF≌△ADF，
∴ ，
在 中， ，
∴ ，
∴ ．
【点睛】
本题主要考查了矩形的性质，全等三角形的判定和性质，勾股定理等知识，熟练掌握矩形的性质，全等三角形的判定和性质，勾股定理是解题的关键．
3、 (1)证明见解析
(2)10
【解析】
【分析】
（1）利用AC平分∠BAD，AB∥CD，得到∠DAC＝∠DCA，即可得到AD＝DC，利用一组对边平行且相等可证明四边形ABCD是平行四边形，再结合AB＝AD，即可求证结论；
（2）根据菱形的性质，得到CD＝13，AO＝CO＝12，结合中位线性质，可得四边形BDEG是平行四边形，利用勾股定理即可得到OB、OD的长度，即可求解．
(1)
证明：∵AC平分∠BAD，AB∥CD，
∴∠DAC＝∠BAC，∠DCA＝∠BAC，
∴∠DAC＝∠DCA，
∴AD＝DC，
又∵AB∥CD，AB＝AD，
∴AB∥CD且AB＝CD，
∴四边形ABCD是平行四边形，
∵AB＝AD，
∴四边形ABCD是菱形．
(2)
解：连接BD，交AC于点O，如图：

∵菱形ABCD的边长为13，对角线AC＝24，
∴CD＝13，AO＝CO＝12，
∵点E、F分别是边CD、BC的中点，
∴EF∥BD（中位线），
∵AC、BD是菱形的对角线，
∴AC⊥BD，OB＝OD，
又∵AB∥CD，EF∥BD，
∴DE∥BG，BD∥EG，
∵四边形BDEG是平行四边形，
∴BD＝EG，
在△COD中，
∵OC⊥OD，CD＝13，CO＝12，
∴，
∴EG＝BD＝10．
【点睛】
本题考查了平行四边形性质判定方法、菱形的判定和性质、等腰三角形性质、勾股定理等知识，关键在于熟悉四边形的判定方法和在题目中找到合适的判定条件．
4、 (1)见解析
(2)见解析
【解析】
【分析】
（1）直接利用线段垂直平分线的作法得出答案；
（2）结合垂直平分线的性质得出△ADE≌△FBE，即可得出AE=EF，进而利用菱形的判定方法得出答案．
(1)
（1）如图：EF即为所求作

(2)
证明：如图，连接DF，
∵AD//BC，
∴∠ADE=∠EBF，
∵AF垂直平分BD，
∴BE=DE．
在△ADE和△FBE中，
，
∴△ADE≌△FBE（ASA），
∴AE=EF，
∴BD与AF互相垂直且平分，
∴四边形ABFD为菱形．
【点睛】
此题主要考查了菱形的判定以及线段垂直平分线的性质与作法，正确应用线段垂直平分线的性质是解题关键．
5、 (1)见解析
(2)当AD=AB时，四边形BEDH是正方形
【解析】
【分析】
（1）要证明AF=CG，只要证明△EAF≌△HCG即可；
（2）利用已知可得四边形BEDH是菱形，所以当AE2+DE2=AD2时，∠BED=90°，四边形BEDH是正方形．
(1)
证明：∵四边形ABCD是平行四边形，
∴AB∥CD，AB=CD，∠BAD=∠BCD，
∴∠AEF=∠CHG，
∵BE=2AB，DH=2CD，
∴BE=DH，
∴BE-AB=DH-DC，
∴AE=CH，
∴∠BAD+∠EAF=180°，∠BCD+∠GCH=180°，
∴∠EAF=∠GCH，
∴△EAF≌△HCG(ASA)，
∴AF=CG；
(2)
解：当AD=AB时，四边形BEDH是正方形；
理由：∵BE∥DH，BE=DH，
∴四边形EBHD是平行四边形，
∵EH⊥BD，
∴四边形EBHD是菱形，
∴ED=EB=2AB，
当AE2+DE2=AD2时，则∠BED=90°，
∴四边形BEDH是正方形，即AB2+(2AB)2=AD2，
∴AD=AB，
∴当AD=AB时，四边形BEDH是正方形．
．
【点睛】
本题考查了正方形的判定，菱形的判定，平行四边形的性质，全等三角形的判定与性质，结合图形分析并熟练掌握正方形的判定，平行四边形的性质，是解题的关键．