沪科版八年级下册17.3 一元二次方程的根的判别式教学演示课件ppt

这是一份沪科版八年级下册17.3 一元二次方程的根的判别式教学演示课件ppt，共20页。PPT课件主要包含了学习目标及重难点，课程导入，课程讲授，两个不相等实数根，两个相等实数根，没有实数根，两个实数根，判别式的情况，根的情况，特别指出等内容，欢迎下载使用。
1.理解并掌握一元二次方程根的判别式的概念；2.会用判别式判断一元二次方程的根的情况；3.根据一元二次方程的根的情况确定字母的取值范围.（重点、难点）
放学了，同学们在一起讨论一元二次方程根的情况.
通过配方，我们得到了一元二次方程ax2+bx+c=0(a≠0)的求根公式，因为a≠0，所以
探索1：一元二次方程根的判别式
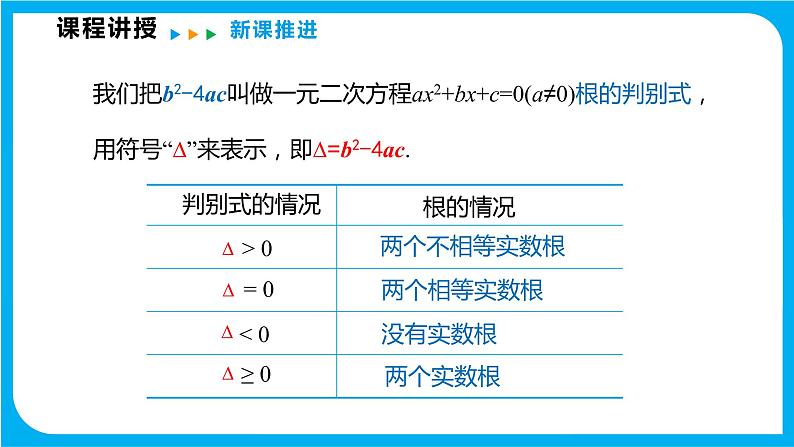
我们把b2-4ac叫做一元二次方程ax2+bx+c=0(a≠0)根的判别式，用符号“∆”来表示，即∆=b2-4ac.
特别指出：当 ∆≥0时，有两个实数根.
当方程有两个实数根时，
不解方程，判别下列方程根的情况.
探索2：根的判别式的应用
解：(1)因为Δ＝(－3)2－4×5×(－2)＝49＞0, 所以原方程有两个不相等的实数根.
(1)5x2－3x－2＝0；
(2)原方程可变形为 25y2－20y＋4＝0. 因为 Δ＝(－20)2－4×25×4＝0， 所以原方程有两个相等的实数根.
(2)25y2＋4＝20y；
解：∵方程kx2－12x＋9＝0是关于x的一元二次方程，∴k≠0.方程根的判别式Δ＝(－12)2－4k×9＝144－36k.由144－36k＞0，求得k＜4，又 k≠0，∴当k＜4且k≠0时，方程有两个不相等的实数根．
根的判别式的应用：(1)直用：不解方程，可以判断方程根的情况．(2)逆用：已知方程根的情况，判断字母系数的取值范围．
1. 下列一元二次方程中,没有实数根的是(　　)A.x2-2x=0 B.x2+4x-1=0C.2x2-4x+3=0 D.3x2=5x-2
2. 若关于x的一元二次方程(k－1)x2＋4x＋1＝0有两个不相等的实数根，则k的取值范围是(　　)A．k＜5 B．k＜5，且k≠1C．k≤5，且k≠1 D．k＞5
不解方程,判断下列一元二次方程根的情况.
解:(1)∵a=9,b=6,c=1,∴b2-4ac=36-36=0,∴此方程有两个相等的实数根.
(2)将一元二次方程化为一般形式,得2x2-x-6=0.∵a=2,b=-1,c=-6,∴b2-4ac=(-1)2-4×2×(-6)=49>0,∴此方程有两个不相等的实数根.
(3)x2-x+1=0，a=1,b=-1,c=1.∴b2-4ac=(-1)2-4×1×1=-30