第六章 第二节 与圆有关的位置关系课件PPT

这是一份第六章 第二节 与圆有关的位置关系课件PPT，共13页。PPT课件主要包含了切线的判定与性质，知识点2，三角形的内切圆，知识点3，角平分线，命题点1，命题点2，命题规律，重难点突破，能力关等内容，欢迎下载使用。
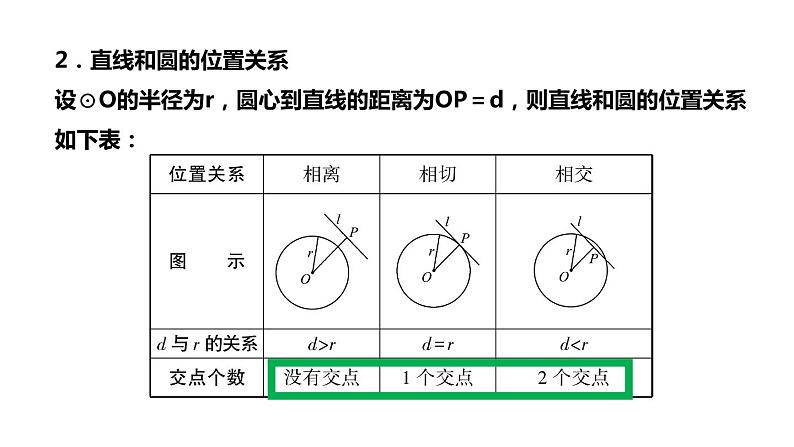
2．直线和圆的位置关系设⊙O的半径为r，圆心到直线的距离为OP＝d，则直线和圆的位置关系如下表：
1．切线：直线和圆有_______的公共点(即直线和圆相切)时，这条直线叫做圆的切线，这个唯一的公共点叫做切点．2．切线的性质：圆的切线_______于过切点的半径．
3．切线的判定(1)定义判定：和圆有_______公共点的直线是圆的切线．(2)数量关系：圆心到直线的距离等于_______的直线是圆的切线．(3)定理：过半径外端且_______于半径的直线是圆的切线．4．切线长：过圆外一点画圆的切线，这点和切点之间的线段长叫做这点到圆的切线长．5．切线长定理：过圆外一点所画的圆的两条切线长相等．
1．和三角形三边都________的圆叫做三角形的内切圆，内切圆的圆心叫做三角形的内心．2．三角形的内心是三角形的三条___________的交点，它到三角形三边的距离相等．[拓展]三角形的外心是三条垂直平分线的交点，它到三角形三个端点的距离相等3．三角形的内心在三角形的内部．
三角形内切圆半径与三角形三边关系 若已知⊙O是△ABC的内切圆，三角形三边长分别为a，b，c，面积为S，圆的半径为r，则r＝2S/a+b+c.特别地，当△ABC是直角三角形，∠C＝90°时，r＝1/2(a＋b－c)．
例1 (2020·广东广州)如图，Rt△ABC中，∠C＝90°，AB＝5，cs A＝ ，以点B为圆心，r为半径作⊙B，当r＝3时，⊙B与AC的位置关系是(　　)　　　A．相离 B．相切C．相交 D．无法确定
点、直线与圆的位置关系 (10年2考)
【思路分析】 根据三角函数的定义得到AC，根据勾股定理求得BC，再与⊙B的半径比较即可．
练 (2020·上海)在矩形ABCD中，AB＝6，BC＝8，点O在对角线AC上，⊙O的半径为2，如果⊙O与矩形ABCD的各边都没有公共点，那么线段AO长的取值范围是_____________．
例2 如图，在扇形CAB中，CD⊥AB，垂足为D，⊙E是△ACD的内切圆，连接AE，BE，则∠AEB的度数为 .
三角形的内切圆 (10年0考)
与切线有关的证明及计算 (10年10考)
2．方法点拨：切线证明的常见模型有三种：①弦切角模型；②平行线＋角平分线模型；③双切线模型．本题以平行线＋角平分线模型为背景，在此基础上进行演变，可变式成弦切角模型、双切线模型，旨在通过一个题目的变形，掌握切线判定的方法．
考法❶　与切线判定有关的证明及计算 (2020·枣庄)如图，在△ABC中，AB＝AC，以AB为直径的⊙O分别交AC，BC于点D，E，点F在AC的延长线上，且∠BAC＝2∠CBF.(1)求证： BF是⊙O的切线；(2)若⊙O的直径为4, CF＝6，求tan∠CBF.
考法❷　与切线性质有关的证明及计算 (2021·枣庄)如图，⊙O是△ABC的外接圆，点O在BC边上，∠BAC的平分线交⊙O于点D，连接BD，CD，过点D作⊙O的切线与AC的延长线交于点P.(1)求证：DP∥BC；(2)求证：△ABD∽△DCP；(3)当AB＝5 cm，AC＝12 cm时，求线段PC的长．
1.(2019·枣庄)如图，在Rt△ABC中，∠ABC＝90°，以AB为直径作⊙O，D为⊙O上一点，且CD＝CB，连接DO并延长交CB的延长线于点E.(1)判断直线CD与⊙O的位置关系，并说明理由；(2)若BE＝2，DE＝4，求圆的半径及AC的长．