初中数学18.2.2 菱形图片课件ppt

这是一份初中数学18.2.2 菱形图片课件ppt，共28页。PPT课件主要包含了学习目标，对边平行且相等，对角相等邻角互补，对角线互相平分，中心对称图形，复习回顾，平行四边形，知识精讲，生活中的实例，探究活动等内容，欢迎下载使用。
了解菱形的概念及其与平行四边形的关系.探索并证明菱形的性质定理.
应用菱形的性质定理解决相关计算或证明问题.
平行四边形有哪些性质？
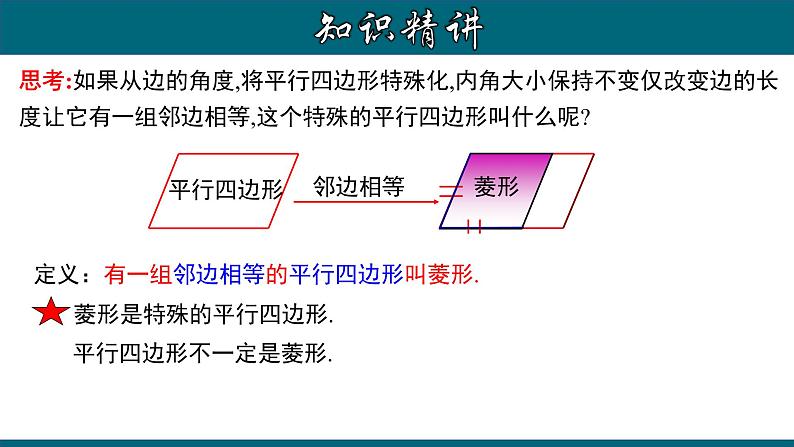
思考:如果从边的角度,将平行四边形特殊化,内角大小保持不变仅改变边的长度让它有一组邻边相等,这个特殊的平行四边形叫什么呢?
平行四边形不一定是菱形.
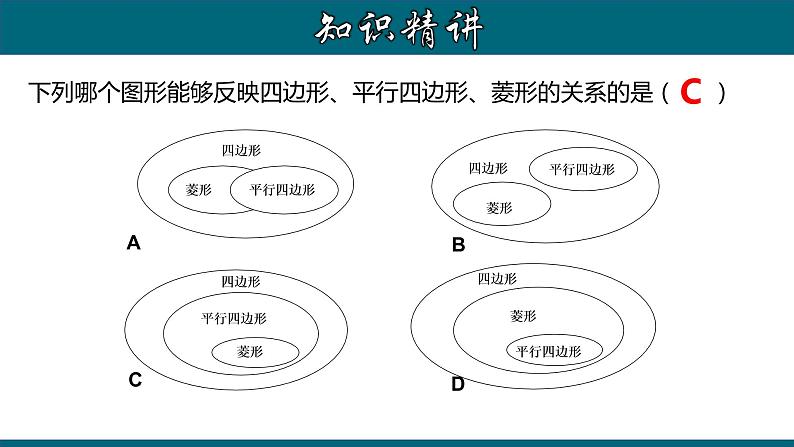
下列哪个图形能够反映四边形、平行四边形、菱形的关系的是（ ）
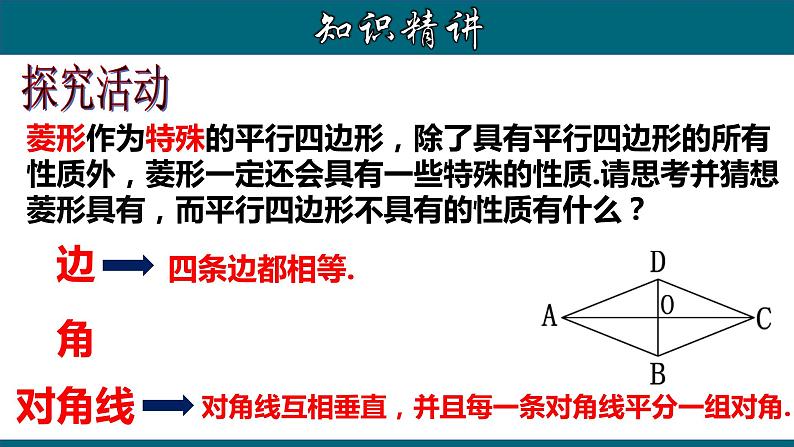
菱形作为特殊的平行四边形，除了具有平行四边形的所有性质外，菱形一定还会具有一些特殊的性质.请思考并猜想菱形具有，而平行四边形不具有的性质有什么？
对角线互相垂直，并且每一条对角线平分一组对角.
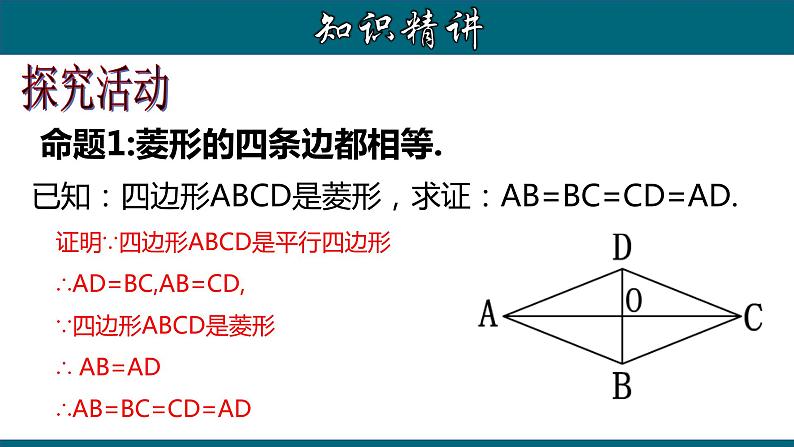
命题1:菱形的四条边都相等.
已知：四边形ABCD是菱形，求证：AB=BC=CD=AD.
证明∵四边形ABCD是平行四边形∴AD=BC,AB=CD,∵四边形ABCD是菱形∴ AB=AD∴AB=BC=CD=AD
菱形性质定理1：菱形的四条边都相等.
∵四边形ABCD是菱形∴AB=BC=CD=AD
命题2:菱形的对角线互相垂直，并且每一条对角线平分一组对角.
已知：如图,菱形ABCD的对角线AC和BD相交于点O.求证：AC⊥BD ;AC平分∠BAD和∠BCD ；BD平分∠ABC和∠ADC
证明：∵四边形ABCD是菱形
又∵在△ABD中，BO=DO
∴AC⊥BD，AC平分∠BAD
同理： AC平分∠BCD；BD平分∠ABC和∠ADC
菱形性质定理2：菱形的对角线互相垂直，并且每一 条对角线平分一组对角.
∵四边形ABCD是菱形∴AC⊥BD，AC平分∠BAD和∠BCD ；BD平分∠ABC和∠ADC
菱形是特殊的平行四边形，它除具有平行四边形的所有性质外，还有平行四边形所没有的特殊性质.
对称性：是轴对称图形.边：四条边都相等.对角线：互相垂直，且每条对角线平分一组对角.
角：对角相等.边：对边平行且相等.对角线：相互平分.
例1 如图，在菱形ABCD中，对角线AC、BD相交于点O，BD＝12cm，AC＝6cm，求菱形的周长．
解：∵四边形ABCD是菱形，∴AC⊥BD，AO＝ AC，BO＝ BD.∵AC＝6cm，BD＝12cm，∴AO＝3cm，BO＝6cm.在Rt△ABO中，由勾股定理得∴菱形的周长＝4AB＝4×3 ＝12 (cm)．
例2 如图，在菱形ABCD中，CE⊥AB于点E，CF⊥AD于点F，求证：AE＝AF.
证明：连接AC. ∵四边形ABCD是菱形， ∴AC平分∠BAD， 即∠BAC＝∠DAC. ∵CE⊥AB，CF⊥AD， ∴∠AEC＝∠AFC＝90°. 又∵AC＝AC， ∴△ACE≌△ACF. ∴AE＝AF.
【点睛】菱形是轴对称图形，它的两条对角线所在的直线都是它的对称轴，每条对角线平分一组对角．
例3 如图，E为菱形ABCD边BC上一点，且AB=AE，AE交BD于O，且∠DAE=2∠BAE，求证：OA=EB.
证明：∵四边形ABCD为菱形，∴AD∥BC，AD=BA， ∠ABC＝∠ADC＝2∠ADB ，∴∠DAE＝∠AEB，∵AB=AE,∴∠ABC＝∠AEB， ∴∠ABC=∠DAE， ∵∠DAE＝2∠BAE，∴∠BAE＝∠ADB. 又∵AD＝BA ，∴△AOD≌△BEA ，∴AO＝BE .
1.如图，在菱形ABCD中，已知∠A＝60°，AB＝5，则△ABD的周长是 (　　) A.10 B.12 C.15 D.20
2.如图，菱形ABCD的周长为48cm，对角线AC、BD相交于O点，E是AD的中点，连接OE，则线段OE的长为_______.
问题1 菱形是特殊的平行四边形,那么能否利用平行四边形面积公式计算菱形ABCD的面积吗?
思考 前面我们已经学习了菱形的对角线互相垂直,那么能否利用对角线来计算菱形ABCD的面积呢?
能.过点A作AE⊥BC于点E,则S菱形ABCD=底×高 =BC·AE.
问题2 如图，四边形ABCD是菱形，对角线AC，BD交于点O,试用对角线表示出菱形ABCD的面积.
解：∵四边形ABCD是菱形，∴AC⊥BD,∴S菱形ABCD=S△ABC +S△ADC= AC·BO+ AC·DO= AC(BO+DO)= AC·BD.
菱形的面积 = 底×高 = 对角线乘积的一半
例4 如图，在菱形ABCD中，点O为对角线AC与BD的交点，且在△AOB中，OA＝5，OB＝12.求菱形ABCD两对边的距离h.
解：在Rt△AOB中，OA＝5，OB＝12，∴S△AOB＝ OA·OB＝ ×5×12＝30，∴S菱形ABCD＝4S△AOB＝4×30＝120.∵又∵菱形两组对边的距离相等，∴S菱形ABCD＝AB·h＝13h，∴13h＝120，得h＝ .
【点睛】菱形的面积计算有如下方法：(1)一边长与两对边的距离(即菱形的高)的积；(2)四个小直角三角形的面积之和(或一个小直角三角形面积的4倍)；(3)两条对角线长度乘积的一半．
例5 如图，菱形花坛ABCD的边长为20m，∠ABC＝60°，沿着菱形的对角线修建了两条小路AC和BD，求两条小路的长和花坛的面积（结果分别精确到0.01m和0.1m2 ）.
解：∵花坛ABCD是菱形，
如图，在菱形ABCD中，∠ABC与∠BAD的度数比为1：2，周长是8cm．求：（1）两条对角线的长度；（2）菱形的面积．
解：（1）∵四边形ABCD是菱形，∴AB=BC，AC⊥BD，AD∥BC，∴∠ABC+∠BAD=180°.∵∠ABC与∠BAD的度数比为1：2，∴∠ABC= ×180°=60°，∴∠ABO= ×∠ABC=30°，△ABC是等边三角形.∵菱形ABCD的周长是8cm．∴AB=2cm，
∴OA= AB=1cm，AC=AB=2cm， ∴BD=2OB= cm；（2）S菱形ABCD= AC•BD = ×2× = （cm2）．
【点睛】 菱形中的相关计算通常转化为直角三角形或等腰三角形，当菱形中有一个角是60°时，菱形被分为以60°为顶角的两个等边三角形.
3.如图，已知菱形的两条对角线分别为6cm和8cm，则这个菱形的高DE为（　　） C.5cm
4.如图，菱形ABCD的边长为4cm，∠BAD＝120°。对角线AC、BD相交于点O，求这个菱形的对角线长和面积.
∴ △ BAC是等边三角形
∴ AC＝AB= 4cm
解：∵ 四边形ABCD为菱形
∵ ∠BAD＝120°
∴AD∥BC，AC⊥BD，AB=BC
有一组邻边相等的平行四边形叫做菱形。
菱形是特殊的平行四边形。
（2）菱形的四条边都相等。
（3）菱形的对角线互相垂直，并且每一 条对角线平分一组对角。
（1）具备平行四边形的所有性质。