

2021-2022学年贵州省毕节市七年级(上)期末数学试卷 解析版
展开2021-2022学年贵州省毕节市七年级(上)期末数学试卷
一、选择题(每小题3分,共45分)
1.(3分)用黑板擦刷黑板时,留下的痕迹是( )
A.点 B.线 C.面 D.体
2.(3分)方程﹣2x=6的解是( )
A.x=2 B.x=﹣3 C.x=﹣2 D.x=﹣12
3.(3分)为了反映今天的气温变化情况,你认为选择哪种统计图最恰当( )
A.频数分布直方图 B.条形统计图
C.扇形统计图 D.折线统计图
4.(3分)虚拟货币比特币,其发行量为12050000枚,用科学记数法表示12050000正确的是( )
A.1.205×107 B.1.20×108 C.1.21×107 D.1.205×104
5.(3分)检测足球时,超过标准质量的克数记为正数,不足标准质量的克数记为负数.从轻重的角度看,下图中最接近标准的是( )
A. B. C. D.
6.(3分)一个多项式与a2﹣2a+1的和是3a﹣2,则这个多项式为( )
A.a2﹣5a+3 B.﹣a2+5a﹣3 C.a2﹣5a﹣13 D.﹣a2+a﹣1
7.(3分)下列各对数中,互为相反数的是( )
A.﹣(+1)和+(﹣1) B.﹣(﹣1)和+(﹣1)
C.﹣(+1)和﹣1 D.+(﹣1)和﹣1
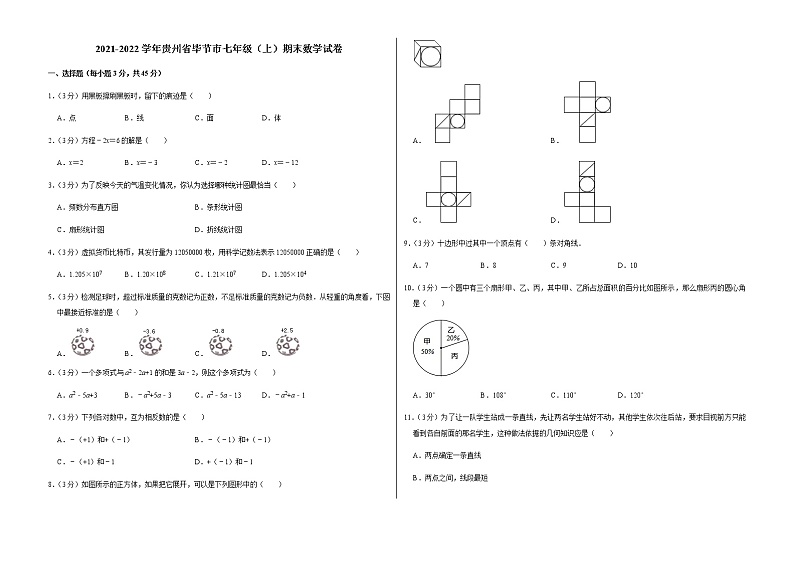
8.(3分)如图所示的正方体,如果把它展开,可以是下列图形中的( )
A. B.
C. D.
9.(3分)十边形中过其中一个顶点有( )条对角线.
A.7 B.8 C.9 D.10
10.(3分)一个圆中有三个扇形甲、乙、丙,其中甲、乙所占总面积的百分比如图所示,那么扇形丙的圆心角是( )
A.30° B.108° C.110° D.120°
11.(3分)为了让一队学生站成一条直线,先让两名学生站好不动,其他学生依次往后站,要求目视前方只能看到各自前面的那名学生,这种做法依据的几何知识应是( )
A.两点确定一条直线
B.两点之间,线段最短
C.射线只有一个端点
D.两直线相交只有一个交点
12.(3分)钟表10点30分时,时针与分针所成的角是( )
A.120° B.135° C.150° D.225°
13.(3分)下列调查中,最适合采用普查方式的是( )
A.调查某品牌电视的使用寿命
B.调查毕节市元旦当天进出主城区的车流量
C.调查我校七(1)班新冠核酸检查结果
D.调查某批次烟花爆竹的燃放效果
14.(3分)已知(a﹣1)2+|b+2|=0,则(a+b)2022的值是( )
A.﹣1 B.1 C.2 D.3
15.(3分)下列图形都是由同样大小的小圆圈按一定规律所组成的,其中第①个图形中一共4个小圆圈,第②个图形中一共有10个小圆圈,第③个图形中一共有19个小圆圈,…按此规律排列,则第⑥个图形中小圆圈的个数为( )
A.46 B.64 C.75 D.77
二、填空题(每小题5分,共25分)
16.(5分)2021的相反数的绝对值是 .
17.(5分)数轴上点A表示的有理数是﹣5,那么到点A的距离为10的点表示的数是 .
18.(5分)如果3x2ny3与﹣2x4ym+1是同类项,则m﹣n= .
19.(5分)已知a+3b﹣4=0,则9b+3a﹣11的值是 .
20.(5分)若干个相同的小正方体组成的几何体的主视图和左视图如图所示,则组成这个几何体的小正方体最多为 个.
三、解答题(7小题,共80分)
21.(10分)计算:
(1)﹣22+|3﹣5|﹣(﹣3).
(2)(﹣)÷(﹣)2+(﹣0.4)×2.
22.(10分)解下列方程:
(1)11﹣3(2x﹣1)=x;
(2)﹣=1.
23.(10分)先化简,再求值:4(x2﹣xy﹣y2)﹣3(x2﹣y2)+4xy,其中x=﹣2,y=1.
24.(10分)以45千克为七年级学生的标准体重测量7名学生的体重,把超过标准体重的千克数记为正数,不足的千克数记为负数,将其体重记录如下表:
学生(号)
1
2
3
4
5
6
7
与标准体重之差(千克)
﹣5
+3
+2
﹣1
﹣2
+4
+6
(1)最接近标准体重的是学生 (填序号).
(2)最大体重与最小体重相差 千克.
(3)求7名学生的平均体重.
25.(12分)如图,点C是线段AB上一点,M、N分别是AB、CB的中点,AC=10cm,NB=6cm.
(1)求CM的长;
(2)求MN的长.
26.(12分)七星关区和大方两地相距60千米,甲从七星关区出发,每小时行14千米,乙从大方出发,每小时行16千米.
(1)若甲、乙两人同时出发相向而行,则经过多少小时两人相遇?
(2)若甲、乙两人同时出发相向而行,则经过多少小时两人相距15千米?
27.(16分)如图,点O为直线AB上一点,∠BOC=40°,OD平分∠AOC.
(1)求∠AOD的度数:
(2)作射线OE,使∠BOE=∠COE,求∠COE的度数.
2021-2022学年贵州省毕节市七年级(上)期末数学试卷
参考答案与试题解析
一、选择题(每小题3分,共45分)
1.(3分)用黑板擦刷黑板时,留下的痕迹是( )
A.点 B.线 C.面 D.体
【分析】根据点动成线,线动成面,面动成体的原理即可解.
【解答】解:黑板擦属于体,但留下的痕迹是表现在平面上而不是空间的,所以是面.
故选:C.
2.(3分)方程﹣2x=6的解是( )
A.x=2 B.x=﹣3 C.x=﹣2 D.x=﹣12
【分析】把方程﹣2x=6的两边同时除以﹣2,求出x的值是多少即可.
【解答】解:∵﹣2x=6,
∴x=﹣3.
故选:B.
3.(3分)为了反映今天的气温变化情况,你认为选择哪种统计图最恰当( )
A.频数分布直方图 B.条形统计图
C.扇形统计图 D.折线统计图
【分析】扇形统计图表示的是部分在总体中所占的百分比,但一般不能直接从图中得到具体的数据;折线统计图表示的是事物的变化情况;条形统计图能清楚地表示出每个项目的具体数目;依此即可求解.
【解答】解:为了反映今天的气温变化情况,应制作的统计图是折线统计图.
故选:D.
4.(3分)虚拟货币比特币,其发行量为12050000枚,用科学记数法表示12050000正确的是( )
A.1.205×107 B.1.20×108 C.1.21×107 D.1.205×104
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
【解答】解:12050000=1.205×107.
故选:A.
5.(3分)检测足球时,超过标准质量的克数记为正数,不足标准质量的克数记为负数.从轻重的角度看,下图中最接近标准的是( )
A. B. C. D.
【分析】根据题意,知绝对值最小的即为最接近标准的足球.
【解答】解:|﹣0.8|<|+0.9|<|+2.5|<|﹣3.6|,
故选:C.
6.(3分)一个多项式与a2﹣2a+1的和是3a﹣2,则这个多项式为( )
A.a2﹣5a+3 B.﹣a2+5a﹣3 C.a2﹣5a﹣13 D.﹣a2+a﹣1
【分析】直接利用整式的加减运算法则计算得出答案.
【解答】解:∵一个多项式与a2﹣2a+1的和是3a﹣2,
∴这个多项式为:3a﹣2﹣(a2﹣2a+1)=﹣a2+5a﹣3.
故选:B.
7.(3分)下列各对数中,互为相反数的是( )
A.﹣(+1)和+(﹣1) B.﹣(﹣1)和+(﹣1)
C.﹣(+1)和﹣1 D.+(﹣1)和﹣1
【分析】先化简各数,然后根据相反数的定义判断即可.
【解答】解:A、﹣(+1)=﹣1,+(﹣1)=﹣1,不是相反数,故此选项不符合题意;
B、﹣(﹣1)=1,+(﹣1)=﹣1,是相反数,故此选项符合题意;
C、﹣(+1)=﹣1,不是相反数,故此选项不符合题意;
D、+(﹣1)=﹣1,不是相反数,故此选项不符合题意;
故选:B.
8.(3分)如图所示的正方体,如果把它展开,可以是下列图形中的( )
A. B.
C. D.
【分析】根据正方体的展开图的特征,“对面”“邻面”之间的关系进行判断即可.
【解答】解:由“相间Z端是对面”可知A、D不符合题意,而C折叠后,圆形在前面,正方形在上面,则三角形的面在右面,与原图不符,
只有B折叠后符合,
故选:B.
9.(3分)十边形中过其中一个顶点有( )条对角线.
A.7 B.8 C.9 D.10
【分析】根据从任意一个n边形的一个顶点出发可得的对角线的条数为(n﹣3)条解决此题.
【解答】解:∵从任意一个n边形的一个顶点出发可得的对角线的条数为(n﹣3)条,
∴十边形中过其中一个顶点有7条对角线.
故选:A.
10.(3分)一个圆中有三个扇形甲、乙、丙,其中甲、乙所占总面积的百分比如图所示,那么扇形丙的圆心角是( )
A.30° B.108° C.110° D.120°
【分析】根据扇形统计图的意义可得,扇形丙的圆心角占360°的30%,计算即可得答案.
【解答】解:360°×(1﹣50%﹣20%)
=360°×30%
=108°,
故选:B.
11.(3分)为了让一队学生站成一条直线,先让两名学生站好不动,其他学生依次往后站,要求目视前方只能看到各自前面的那名学生,这种做法依据的几何知识应是( )
A.两点确定一条直线
B.两点之间,线段最短
C.射线只有一个端点
D.两直线相交只有一个交点
【分析】先让两个同学站好,实质是确定两定点,而由两点即可确定一条直线.
【解答】解:由题意可知:两点确定一条直线,
故选:A.
12.(3分)钟表10点30分时,时针与分针所成的角是( )
A.120° B.135° C.150° D.225°
【分析】根据时钟上一大格是30°进行计算即可解答.
【解答】解:由题意得:
4×30°+×30°=135°,
∴钟表10点30分时,时针与分针所成的角是:135°,
故选:B.
13.(3分)下列调查中,最适合采用普查方式的是( )
A.调查某品牌电视的使用寿命
B.调查毕节市元旦当天进出主城区的车流量
C.调查我校七(1)班新冠核酸检查结果
D.调查某批次烟花爆竹的燃放效果
【分析】根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似解答.
【解答】解:A.调查某品牌电视的使用寿命,适合抽样调查,此选项不符合题意;
B.调查毕节市元旦当天进出主城区的车流量,适合抽样调查,此选项不符合题意;
C.调查我校七(1)班新冠核酸检查结果,适合采用普查方式,故本选项符合题意;
D.调查某批次烟花爆竹的燃放效果,适合抽样调查,此选项不符合题意;
故选:C.
14.(3分)已知(a﹣1)2+|b+2|=0,则(a+b)2022的值是( )
A.﹣1 B.1 C.2 D.3
【分析】直接利用非负数的性质得出a,b的值,进而得出答案.
【解答】解:∵(a﹣1)2+|b+2|=0,而(a﹣1)2≥0,|b+2|≥0,
∴a﹣1=0,b+2=0,
解得:a=1,b=﹣2,
则(a+b)2022=(1﹣2)2022=1.
故选:B.
15.(3分)下列图形都是由同样大小的小圆圈按一定规律所组成的,其中第①个图形中一共4个小圆圈,第②个图形中一共有10个小圆圈,第③个图形中一共有19个小圆圈,…按此规律排列,则第⑥个图形中小圆圈的个数为( )
A.46 B.64 C.75 D.77
【分析】观察图形特点,从中找出规律,小圆圈的个数分别是3+12,6+22,10+32,15+42,…,总结出其规律为+n2,根据规律求解.
【解答】解:通过观察,得到小圆圈的个数分别是:
第①个图形小圆圈个数为:+12=4,
第②个图形小圆圈个数为:+22=10,
第③个图形小圆圈个数为:+32=19,
第④个图形小圆圈个数为:+42=31,
…,
所以第n个图形小圆圈个数为:+n2,
第⑥个图形小圆圈个数为+62=64,
故选:B.
二、填空题(每小题5分,共25分)
16.(5分)2021的相反数的绝对值是 2021 .
【分析】根据2021的相反数是﹣2021,计算﹣2021的绝对值即可得出答案.
【解答】解:2021的相反数是﹣2021,
|﹣2021|=2021.
故答案为:2021;
17.(5分)数轴上点A表示的有理数是﹣5,那么到点A的距离为10的点表示的数是 ﹣15或5 .
【分析】考虑两种情况:要求的点在已知点A的左侧或右侧.
【解答】解:在数轴上与表示﹣5的点距离10个单位长度的点表示的数是﹣5+10=5或﹣5﹣10=﹣15.
故答案为:﹣15或5.
18.(5分)如果3x2ny3与﹣2x4ym+1是同类项,则m﹣n= 0 .
【分析】利用同类项的定义求出m与n的值,即可确定出m﹣n的值.
【解答】解:根据题意得:2n=4,m+1=3,
解得:m=2,n=2,
则m﹣n=2﹣2=﹣0.
故答案为:0.
19.(5分)已知a+3b﹣4=0,则9b+3a﹣11的值是 1 .
【分析】由a+3b﹣4=0,得a+3b=4,将9b+3a﹣11变形成3(a+3b)﹣11,再整体代入即可得答案.
【解答】解:∵a+3b﹣4=0,
∴a+3b=4,
∴9b+3a﹣11=3(a+3b)﹣11=3×4﹣11=12﹣11=1,
故答案为:1.
20.(5分)若干个相同的小正方体组成的几何体的主视图和左视图如图所示,则组成这个几何体的小正方体最多为 5 个.
【分析】易得此几何体有两行,两列,判断出各行各列最多有几个正方体组成即可.
【解答】解:底层正方体最多有4个正方体,第二层最多有1个正方体,所以组成这个几何体的小正方体的个数最多有5个.
故答案为:5;
三、解答题(7小题,共80分)
21.(10分)计算:
(1)﹣22+|3﹣5|﹣(﹣3).
(2)(﹣)÷(﹣)2+(﹣0.4)×2.
【分析】(1)先算绝对值和乘方,再算加减法;
(2)先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.
【解答】解:(1)原式=﹣4+|﹣2|+3
=﹣4+2+3
=1;
(2)原式=()÷+(﹣)×
=(﹣)×36+(﹣1)
=(﹣1)+(﹣1)
=﹣2.
22.(10分)解下列方程:
(1)11﹣3(2x﹣1)=x;
(2)﹣=1.
【分析】(1)方程去括号,移项,合并同类项,把x系数化为1,即可求出解;
(2)方程去分母,去括号,移项,合并同类项,把x系数化为1,即可求出解.
【解答】解:(1)去括号得:11﹣6x+3=x,
移项合并得:﹣7x=﹣14,
解得:x=2;
(2)去分母得:4(2x﹣1)﹣3(x+1)=12,
去括号得:8x﹣4﹣3x﹣3=12,
移项合并得:5x=19,
解得:x=3.8.
23.(10分)先化简,再求值:4(x2﹣xy﹣y2)﹣3(x2﹣y2)+4xy,其中x=﹣2,y=1.
【分析】原式去括号合并得到最简结果,把x与y的值代入计算即可求出值.
【解答】解:原式=4x2﹣4xy﹣4y2﹣3x2+3y2+4xy
=x2﹣y2,
当x=﹣2,y=1时,
原式=(﹣2)2﹣12=4﹣1=3.
24.(10分)以45千克为七年级学生的标准体重测量7名学生的体重,把超过标准体重的千克数记为正数,不足的千克数记为负数,将其体重记录如下表:
学生(号)
1
2
3
4
5
6
7
与标准体重之差(千克)
﹣5
+3
+2
﹣1
﹣2
+4
+6
(1)最接近标准体重的是学生 4号 (填序号).
(2)最大体重与最小体重相差 11 千克.
(3)求7名学生的平均体重.
【分析】(1)与标准体重之差的绝对值越小,就最接近标准体重,直接观察绝对值最小的数即可;
(2)由表格可知最高体重是第2名学生,最低体重是第1名学生,从而可以求得最高体重与最低体重相差多少;
(3)用标准体重加上七名学生与标准体重之差的平均数,即为七名学生的平均体重.
【解答】解:(1)由表格可知,4号学生的体重与标准体重之差的绝对值最小,
∴最接近标准体重的是4号学生.
故答案为:4号;
(2)由表格可知最高体重是第7号学生,最低体重是第1号学生,
∴体重之差为:6﹣(﹣5)=6+5=11(千克)
故答案为:11;
(3)7名学生的平均体重=45+(﹣5+3+2﹣1﹣2+4+6)÷7=46(千克),
∴7名学生的平均体重为46千克.
25.(12分)如图,点C是线段AB上一点,M、N分别是AB、CB的中点,AC=10cm,NB=6cm.
(1)求CM的长;
(2)求MN的长.
【分析】(1)根据N为BC的中点,NB=6cm,可得BC=2NB的长度,由AC=10cm,可计算出AB=AC+BC的长度,因为M为AB的中点,可得BM=AM=AB的长度,根据CM=AM﹣AC计算即可得出答案;
(2)由(1)得BM=11cm,由NB=6cm根据MN=BM﹣NB代入计算即可得出答案.
【解答】解:(1)∵N为BC的中点,NB=6cm,
∴BC=2NB=2×6=12(cm),
∵AC=10cm,
∴AB=AC+BC=10+12=22(cm),
∵M为AB的中点,
∴BM=AM=AB=×22=11(cm),
∴CM=AM﹣AC=11﹣10=1(cm).
∴线段CM的长为1cm;
(2)由(1)得BM=11(cm),
∵NB=6cm
∴MN=BM﹣NB=11﹣6=5(cm),
∴线段MN的长为5cm.
26.(12分)七星关区和大方两地相距60千米,甲从七星关区出发,每小时行14千米,乙从大方出发,每小时行16千米.
(1)若甲、乙两人同时出发相向而行,则经过多少小时两人相遇?
(2)若甲、乙两人同时出发相向而行,则经过多少小时两人相距15千米?
【分析】(1)设两人同时出发相向而行,需经过x小时两人相遇,根据:甲每小时行的路程×两人相遇用的时间+乙每小时行的路程×两人相遇用的时间=两地之间的距离,列出方程,求出x的值即可.
(2)根据题意,分两种情况:①当两人相遇前相距15千米,②当两人相遇后相距15千米,求出经过多少小时两人相距15千米即可.
【解答】解:(1)设两人同时出发相向而行,需经过x小时两人相遇,
根据题意得:14x+16x=60,
解得:x=2.
答:两人同时出发相向而行,经过2小时两人相遇.
(2)设两人同时出发相向而行,需y小时两人相距15千米,
①当两人相遇前相距15千米,
根据题意得:14y+16y+15=60,
解得:y=1.5.
②当两人相遇后相距15千米,
依题意得14y+16y=60+15,
解得:y=2.5.
答:若甲乙两人同时出发相向而行,则经过1.5小时或2.5小时两人相距15千米.
27.(16分)如图,点O为直线AB上一点,∠BOC=40°,OD平分∠AOC.
(1)求∠AOD的度数:
(2)作射线OE,使∠BOE=∠COE,求∠COE的度数.
【分析】(1)先求出∠AOC的度数,再根据OD平分∠AOC,即可得到∠AOD=∠AOC=70°;
(2)根据题意画出图形,分两种情况分别计算即可.
【解答】解:(1)∵∠BOC=40°,
∴∠AOC=180°﹣∠BOC=140°,
∵OD平分∠AOC,
∴∠AOD=∠AOC=70°;
答:∠AOD的度数为70°;
(2)①如图,当射线OE在AB上方时,∠BOE=∠COE,
∵∠BOE+∠COE=∠BOC,
∴∠COE+∠COE=40°,
∴∠COE=24°;
②如图,当射线OE在AB下方时,∠BOE=∠COE,
∵∠COE﹣∠BOE=∠BOC,
∴∠COE﹣∠COE=40°,
∴∠COE=120°;
综上所述:∠COE的度数为24°或120°.
贵州省毕节市2021-2022学年七年级(上)期中数学试卷(含答案): 这是一份贵州省毕节市2021-2022学年七年级(上)期中数学试卷(含答案),共16页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2021-2022学年贵州省毕节市威宁县八年级(上)期末数学试卷(含解析): 这是一份2021-2022学年贵州省毕节市威宁县八年级(上)期末数学试卷(含解析),共18页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
2021-2022学年贵州省毕节市威宁县九年级(上)期末数学试卷(含解析): 这是一份2021-2022学年贵州省毕节市威宁县九年级(上)期末数学试卷(含解析),共19页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












