初中数学人教版七年级下册5.4 平移课时训练

5.4 平移

一、选择题．

1．把△ABC沿BC方向平移，得到△A'B'C'，随着平移距离的不断增大，△A'B'C'的面积大小变化情况是（　　）

A．增大 B．减小 C．不变 D．不确定

【解答】解：∵△ABC沿BC方向平移，得到△A'B'C'，

∴AA′∥BC，

∴S△A′B'C'＝S△ABC．

故选：C．

2．下列生活现象中，属于平移现象的是（　　）

A．急刹车时汽车在地面滑行 

B．足球在草地上跳动 

C．投影片的文字经投影转换到屏幕上 

D．钟摆的摆动

【解答】解：A．急刹车时汽车在地面滑行，是平移现象；

B．足球在草地上跳动，方向变化，不符合平移的定义，不属于平移；

C．投影片的文字经投影转换到屏幕上，大小发生了变化，不符合平移的定义，不属于平移；

D．钟摆的摆动，不沿直线运动，是旋转运动，不属于平移．

故选：A．

3．在下列图形中，周长最长的是（　　）

A． B． 

C． D．

【解答】解：A、由图形可得其周长大于12cm，

B、由图形可得其周长为：12cm，

C、由图形可得其周长为：12cm，

D、由图形可得其周长为：12cm，

故最长的是A．

故选：A．

4．如图，两个直角三角形重叠在一起，将△ABC沿AB方向平移2cm得到△DEF，CH＝2cm，EF＝4cm，下列结论：①BH∥EF；②AD＝BE；③BD＝CH；④∠C＝∠BHD；⑤阴影部分的面积为6cm2．其中正确的是（　　）

A．①②③④⑤ B．②③④⑤ C．①②③⑤ D．①②④⑤

【解答】解：因为将△ABC沿AB方向平移2cm得到△DEF，CH＝2cm，EF＝4cm，

所以：BC＝BC，AB＝DE，

∴BH∥EF，①正确；

∴AB﹣DB＝DE﹣DB，

∴AD＝BE，②正确；

③∵BC＝EF＝4cm，

∵CH＝2cm，

∴BH＝2cm，

∴BH是△DEF的中位线，

∴DB＝BE＝2cm，

∴BD＝CH＝2cm，正确；

∵BH∥EF，

∴∠BHD＝∠F，

由平移性质可得：∠C＝∠F，

∴∠C＝∠BHD，④正确；

∵阴影部分的面积＝△ABC的面积﹣△DBH的面积＝6cm2．⑤正确；

故选：A．

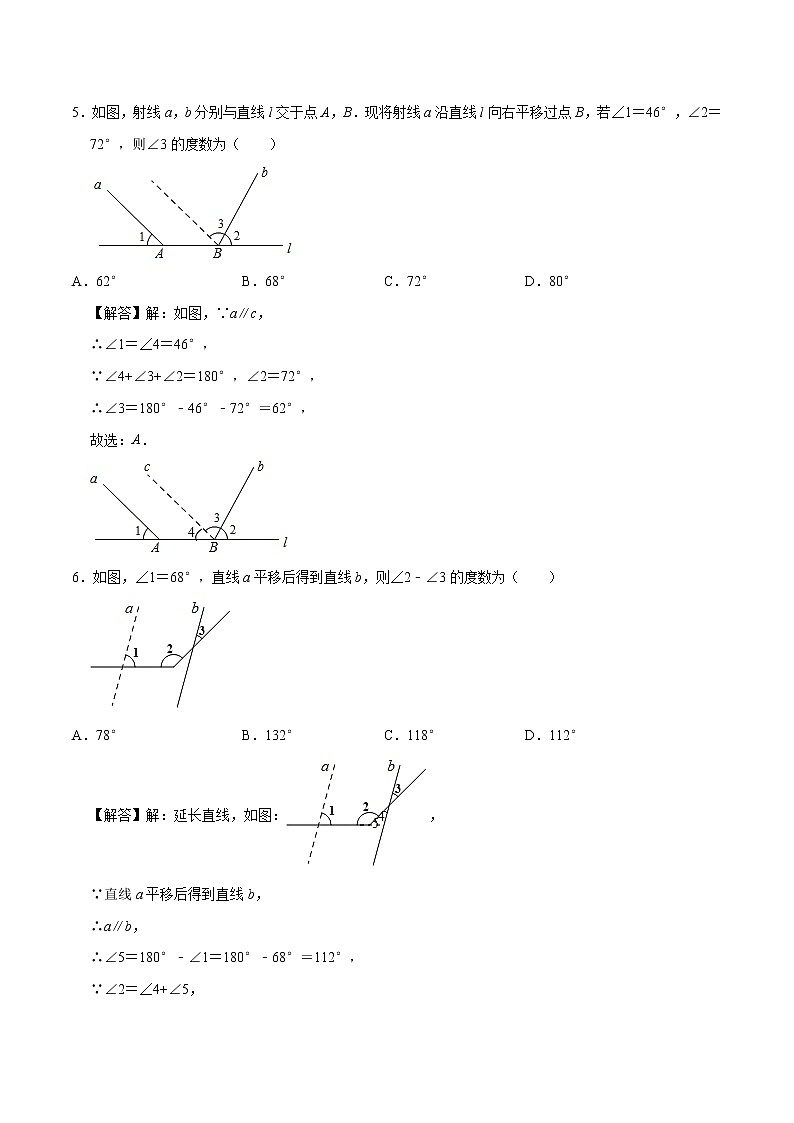
5．如图，射线a，b分别与直线l交于点A，B．现将射线a沿直线l向右平移过点B，若∠1＝46°，∠2＝72°，则∠3的度数为（　　）

A．62° B．68° C．72° D．80°

【解答】解：如图，∵a∥c，

∴∠1＝∠4＝46°，

∵∠4+∠3+∠2＝180°，∠2＝72°，

∴∠3＝180°﹣46°﹣72°＝62°，

故选：A．

6．如图，∠1＝68°，直线a平移后得到直线b，则∠2﹣∠3的度数为（　　）

A．78° B．132° C．118° D．112°

【解答】解：延长直线，如图：，

∵直线a平移后得到直线b，

∴a∥b，

∴∠5＝180°﹣∠1＝180°﹣68°＝112°，

∵∠2＝∠4+∠5，

∵∠3＝∠4，

∴∠2﹣∠3＝∠5＝112°，

故选：D．

二、填空题．

7．如图，将Rt△ABC沿BC方向平移得Rt△DEF，其中AB＝8，BE＝8，DM＝5，则阴影部分的面积是　44　．

【解答】解：∵直角△ABC沿BC方向平移得到直角△DEF，

∴DE＝AB＝8，

∵DM＝5，

∴ME＝DE﹣DM＝8﹣5＝3，

由平移可得：

S阴影＝S△DEF﹣S△MEC

＝S△ABC﹣S△MEC

＝S梯形ABEM

（3+8）×8，

＝44．

故答案为：44．

8．如图，△DEF是由△ABC沿直线BC向右平移得到，若BC＝6，当点E刚好移动到BC的中点时，则CF＝　3　．

【解答】解：由平移的性质可得：BC＝EF，BE＝CF，

∵BC＝6，点E刚好移动到BC的中点，

∴BE＝EC＝CF＝3，

故答案为：3．

9．如图，将直角三角形ABC沿CB方向平移后，得到直角三角形DEF．已知AG＝3，BE＝6，DE＝10，则阴影部分的面积为　51　．

【解答】解：由平移的性质知，AB＝DE＝10，S△ABC＝S△DEF，

∵△GBF为△ABC和△DEF的公共部分，

∴S阴影部分＝S梯形DEBG，

∵∠E＝90°，

∴BE是梯形DEBG的高；

∵BG＝AB﹣AG＝10﹣3＝7，

∴S阴影部分＝S梯形DEBG（7+10）×6＝51．

故答案为：51．

10．如图，将直角三角形ABC沿AB方向平移AD的长度得到三角形DEF，已知BE＝5，EF＝8，CG＝2，则图中阴影部分的面积为　35　．

【解答】解：∵直角三角形ABC沿AB方向平移AD的长度得到三角形DEF，

∴S△ABC＝S△DEF，BC＝EF＝8，

∵CG＝2，

∴BG＝BC﹣CG＝8﹣2＝6，

∴S阴＝S梯形BEFG•（BG+BF）•BE（6+8）×5＝35，

故答案为35．

11．如图，在△ABC中，BC＝3，将△ABC平移5个单位长度得到△A1B1C1，点P、Q分别是AB、A1C1的中点，PQ的最小值等于　　．

【解答】解：取AC的中点M，A1B1的中点N，连接PM，MQ，NQ，PN，

∵将△ABC平移5个单位长度得到△A1B1C1，

∴B1C1＝BC＝3，PN＝5，

∵点P、Q分别是AB、A1C1的中点，

∴NQB1C1，

∴5PQ≤5，

即PQ，

∴PQ的最小值等于，

故答案为：．

12．如图，∠C＝90°，将直角三角形ABC沿着射线BC方向平移6cm，得三角形A′B′C′，已知BC＝3cm，AC＝4cm，则阴影部分的面积为　18　cm2．

【解答】解：由题意平行四边形ABB′A′的面积＝6×4＝24（cm2），S△ABC3×4＝6（cm2），

∴S阴＝S平行四边形ABB′A′﹣S△ABC＝24﹣6＝18（cm2），

故答案为18．

13．如图，将等腰直角△ABC沿BC方向平移得到△A1B1C1，若BC，，则BB1＝　　．

【解答】解：∵△ABC是等腰直角三角形，

∴平移后∠PB1C＝∠B＝45°，

∴△PB1C是等腰直角三角形，

∴S△PB1CB1C•（B1C）＝2，

解得B1C＝2，

∴BB1＝BC﹣B1C＝3．

故答案为：．

14．某宾馆在重新装修后，准备在大厅的主楼梯上铺上红色地毯．已知这种红色地毯的售价为每平方米32元，主楼道宽2米，其侧面如图所示，则购买地毯至少需要　512　元．

【解答】解：利用平移线段，把楼梯的横竖向上向左平移，构成一个矩形，长宽分别为5.5米，2.5米，

∴地毯的长度为2.5+5.5＝8米，地毯的面积为8×2＝16平方米，

∴买地毯至少需要16×32＝512元．

故答案为：512．

三、解答题．

15．在正方形网格中，每个小正方形的边长均为1个单位长度，我们将小正方形的顶点叫做格点，如图，△ABC的三个顶点均在格点上．

（1）将△ABC先向右平移7个单位长度，再向上平移5个单位长度，得到对应的△A1B1C1，画出平移后的△A1B1C1；

（2）请在图中建立适当的平面直角坐标系，使得点A的坐标为（﹣6，3）；

（3）试判断△AB1C的形状，并说明理由．

【解答】解：（1）如图，△A1B1C1为所作；

（2）如图所示，

（3）△AB1C是直角三角形，理由如下：

∴AB12＝12+72＝50，AC2＝32+32＝18，B1C2＝42+42＝32，

∴AB12＝AC2+B1C2，

∴△AB1C是直角三角形．

16．如图，网格中每个小正方形的边长为1个单位长度，三角形ABC中，点A、点B、点C均在格点上．

（1）在图1中，过点C画出线段AB的垂线；

（2）在图1中，过点B画出直线BM，使BM∥AC；

（3）在图2中，先将三角形ABC向右平移5个单位长度，再向上平移4个单位长度，得到三角形A1B1C1，画出三角形A1B1C1．

【解答】解：（1）如图，CD为所作；

（2）如图，BM为所作；

（3）如图，△A1B1C1为所作．

17．南湖公园有很多的长方形草地，草地里修了很多有趣的小路，如图三个图形都是长为50米，宽为30米的长方形草地，且小路的宽都是1米．

（1）如图1，阴影部分为1米宽的小路，长方形除去阴影部分后剩余部分为草地，则草地的面积为　1470平方米　；

（2）如图2，有两条宽均为1米的小路（图中阴影部分），求草地的面积．

（3）如图3，非阴影部分为1米宽的小路，沿着小路的中间从入口E处走到出口F处，所走的路线（图中虚线）长为　108米　．

【解答】解：（1）将小路往左平移，直到E、F与A、B重合，则平移后的四边形EFF1E1是一个矩形，并且EF＝AB＝30，FF1＝EE1＝1，

则草地的面积为：50×30﹣1×30＝1470（平方米）；

故答案为：1470平方米；

（2）小路往AB、AD边平移，直到小路与草地的边重合，

则草地的面积为：（50﹣1）×（30﹣1）＝1421（平方米）；

（3）将小路往AB、AD、DC边平移，直到小路与草地的边重合，

则所走的路线（图中虚线）长为：30﹣1+50+30﹣1＝108（米）．

故答案为：108米．

18．如图，方格纸中每个小正方形的边长均为1．在图中平移三角形ABC，使点A移到点D处，点B的对应点为点E，点C的对应点为点F．

（1）请在方格纸中画出平移后的三角形DEF；

（2）分别连接CD，CF，请直接写出三角形CDF的面积；

（3）过点D作CF的垂线，垂足为H，延长AB交直线DH于点G，请画出图形；直接写出四边形BGHC的面积．

【解答】解：（1）如图所示，△DEF即为所求：

（2）△CDF的面积，

（3）四边形BGHC的面积4.5．

19．如图，将△ABC，向右平移4个格子，再向下平移2个格子．

（1）请你画出经过两次平移后的△DEF（A与D、B与E、C与F对应）；

（2）若每个小正方形的边长为1个单位长度，连接BE和CE，请你求出△BCE的面积．

【解答】解：（1）如图，△DEF即为所求．

（2）S△BCE2×2＝2．

20．如图，在正方形网格中，每个小正方形的边长均为1，格点三角形（顶点是网格线的交点的三角形）ABC的顶点A、C的坐标分别为（﹣4，5）、（﹣1，3）．

（1）请在如图所示的网格平面内画出平面直角坐标系；

（2）点D（m，n）是△ABC边BC上任意一点，三角形经过平移后得到△A1B1C1，点P的对应点为P1（m+6，n﹣2）．

①直接写出点B1的坐标　（4，﹣1）　；

②画出△ABC平移后的△A1B1C1．

（3）在y轴上是否存在点P，使△AOP的面积等于△ABC面积的，若存在，请求出点P的坐标；若不存在，请说明理由．

【解答】解：（1）如图，平面直角坐标系如图所示：

（2）①B1（4，﹣1）．

故答案为（4，﹣1）．

②如图，△A1B1C1即为所求．

（3）设P（0，m）．

由题意，|m|×4（3×42×42×31×2），

解得m＝±，

∴P（0，）或（0，）．

21．如图：在正方形网格中有一个△ABC，按要求进行下列作图（只能借助于网格）．

（1）分别画出△ABC中BC边上的高AH、中线AG．

（2）画出先将△ABC向右平移6格，再向上平移3格后的△DEF．

（3）画一个锐角△MNP（要求各顶点在格点上），使其面积等于△ABC的面积的2倍．

【解答】解：（1）如图所示，AH、AG即为所求；

（2）如图所示，△DEF即为所求；

（3）如图所示，△MNP即为所求．

22．如右图，在每个小正方形边长为1的方格纸中，△ABC的顶点都在方格纸格点上．将△ABC向左平移2格，再向上平移4格．

（1）请在图中画出平移后的△A′B′C′，

（2）再在图中画出△ABC的高CD，

（3）在图中能使S△PBC＝S△ABC的格点P的个数有　4　个（点P异于A）．

【解答】解：（1）如图，△A′B′C′即为所求；

（2）如图，CD即为所求；

（3）如图，P点共有4个．

故答案为：4．

23．如图，已知AB∥CD，点E在直线AB，CD之间．

（1）求证：∠AEC＝∠BAE+∠ECD；

（2）若AH平分∠BAE，将线段CE沿CD平移至FG．

①如图2，若∠AEC＝90°，HF平分∠DFG，求∠AHF的度数；

②如图3，若HF平分∠CFG，试判断∠AHF与∠AEC的数量关系并说明理由．

【解答】解：（1）如图1，过点E作直线EN∥AB，

∵AB∥CD，

∴EN∥CD，

∴∠BAE＝∠AEN，∠DCE＝∠CEN，

∴∠AEC＝∠AEN+∠CEN＝∠BAH+∠ECD；                

（2）∵AH平分∠BAE，

∴∠BAH＝∠EAH，

①∵HF平分∠DFG，设∠GFH＝∠DFH＝x，

又CE∥FG，

∴∠ECD＝∠GFD＝2x，

又∠AEC＝∠BAE+∠ECD，∠AEC＝90°，

∴∠BAH＝∠EAH＝45°﹣x，

如图2，过点H作l∥AB，

易证∠AHF＝∠BAH+∠DFH＝45°﹣x+x＝45°；       

②设∠GFD＝2x，∠BAH＝∠EAH＝y，

∵HF平分∠CFG，

∴∠GFH＝∠CFH＝90°﹣x，

由（1）知∠AEC＝∠BAE+∠ECD＝2x+2y，

如图3，过点H作l∥AB，

易证∠AHF﹣y+∠CFH＝180°，

即∠AHF﹣y+90°﹣x＝180°，∠AHF＝90°+（x+y），

∴∠AHF＝90°∠AEC．（或2∠AHF﹣∠AEC＝180°．）