人教版六年级下册5 数学广角 （鸽巢问题）课堂教学课件ppt

这是一份人教版六年级下册5 数学广角 （鸽巢问题）课堂教学课件ppt，共17页。PPT课件主要包含了教学内容，教学过程，由形抽象到数，计算绝招，温馨提示，板书设计等内容，欢迎下载使用。
人教版六年级数学下册数学广角《抽屉原理》第一课时，也就是教材68-69页的例1和例2. 
深入探究 形成规律
回归生活 灵活应用
组织活动 探究新知
（一）游戏导入 激发兴趣
请五个同学抢坐四把椅子 ，猜猜会有什么样的结果？
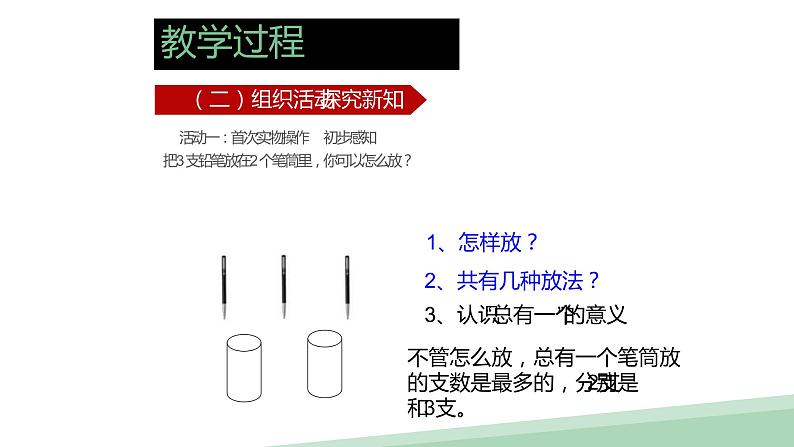
活动一：首次实物操作 初步感知把3支铅笔放在2个笔筒里，你可以怎么放？
（二）组织活动 探究新知
不管怎么放，总有一个笔筒放的支数是最多的，分别是2支和3支。
3、认识“总有一个”的意义 
（１）让学生动手活动：独立思考，怎样解释这一现象？ （２）可以小组合作，实际摆一摆，共有几种情况？ 2、例1 的学习和探索，主要有以下几种方法： （１）借助实物，将４枝铅笔放进３个文具盒中，并把所有可能出现的情况都摆出来。由此发现，把４枝铅笔放进３个文具盒一共有四种情况（课件展示），在每种情况中，都一定有一个文具盒中至少有２枝铅笔。共有四种情况，即（4， 0，0），（3，1，0），（2，2，0），（2，1，1）并板书，每一种结果的三个数中，至少有一个数是不小于2 的。 通过这个例题主要让学生体会“不管”和“至少”两个词的含义，通过刚才的四种情况让学生反复体会。
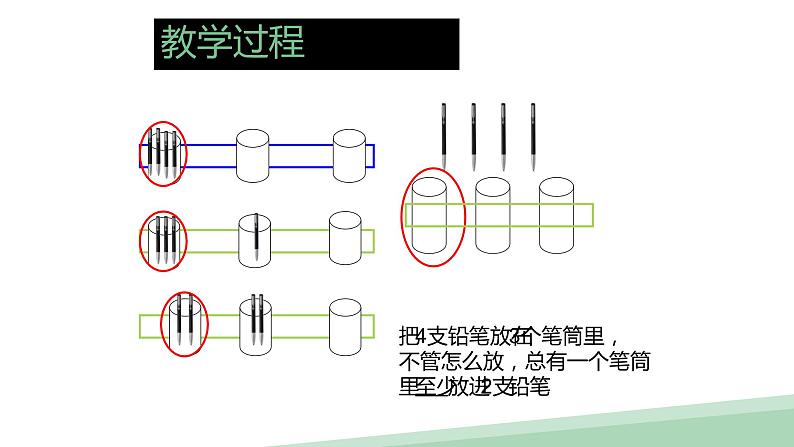
活动二：再次具体操作 深化感知例1、把4支笔放进3个笔筒里，你可以怎么放？
把4支铅笔放在3个笔筒里，不管怎么放，总有一个笔筒里至少放进2支铅笔
活动三：脱离具体操作 由形抽象到数 把6支笔放入5个笔筒中，你能不用动手就很快得到至少数吗？
1、枚举操作自然过渡到平均分的方法。
2、理解“平均分”的思路，知道为什么要“平均分”。
6÷5=1(支）……1（支） 1+1=2（支）
活动四：抽象概括，小结现象 “7支铅笔，放在6个笔筒里”、“ 10支铅笔，放在9个笔筒里”和“100支铅笔，放在99个笔筒里”
归纳概括：当铅笔数比笔筒数多1时，不管怎么放，总有一个笔筒至少放入2支铅笔
例2、把8本书 放进3个抽屉中，不管怎么放，总有一个抽屉至少放进多少本书？为什么？
8÷3=2(本）……2（本）2+1=3（本）
（三）深入探究 形成规律
物体数÷抽屉数=商……余数至少数=商+1
“抽屉原理”又称“鸽巢原理”最先是由19世纪的德国数学家狄利克雷提出来的，所以又称“狄利克雷原理”这一原理在解决实际问题中有着广泛的应用。
狄利克雷（1805～1859）
三个小朋友同行，其中必有两个小朋友性别相同。
（四）回归生活 灵活应用
一幅扑克，拿走大、小王后还有52张牌，请你任意抽出其中的5张牌，猜一猜，会有什么结果？为什么？
小游戏 摸扑克牌
在有些问题中，“抽屉”和“物体”不是很明显,需要我们制造出“抽屉”和“物体”。要能正确地找出题中什么是“物体”，什么是“抽屉”。
抽屉原理铅笔（物体数） 笔筒（抽屉数） 总有一个笔筒里至少有（商+1）支笔 4 ÷ 3= 1…... 1 2 6 ÷ 5 =1…… 1 2 7 ÷ 6 =1 ……1 2 10 ÷ 9 =1 ……1 2 8 ÷ 3 =2…… 2 3 物体数÷抽屉数=商……余数至少数=商+1