六年级下册5 数学广角 （鸽巢问题）教学ppt课件

这是一份六年级下册5 数学广角 （鸽巢问题）教学ppt课件，共23页。PPT课件主要包含了第一种情况，第二种情况，第三种情况，第四种情况，÷311，你发现什么，1﹢1＝2只，尝试练习，合作探究，至少数＝平均数+1等内容，欢迎下载使用。
我给大家表演一个“魔术”。一副牌，取出大小王，还剩52张牌，你们5人每人随意抽一张，我知道至少有2张牌是同花色的，你们相信吗？
想知道我是怎么猜到的吗？
这就是我们这节课要学习的鸽巢问题。
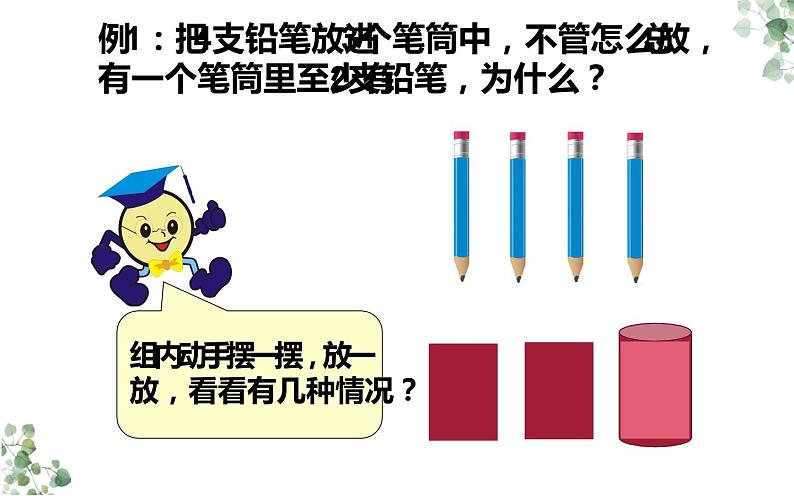
例1：把4支铅笔放进3个笔筒中，不管怎么放，总有一个笔筒里至少有2支铅笔，为什么？
组内动手摆一摆，放一放，看看有几种情况？
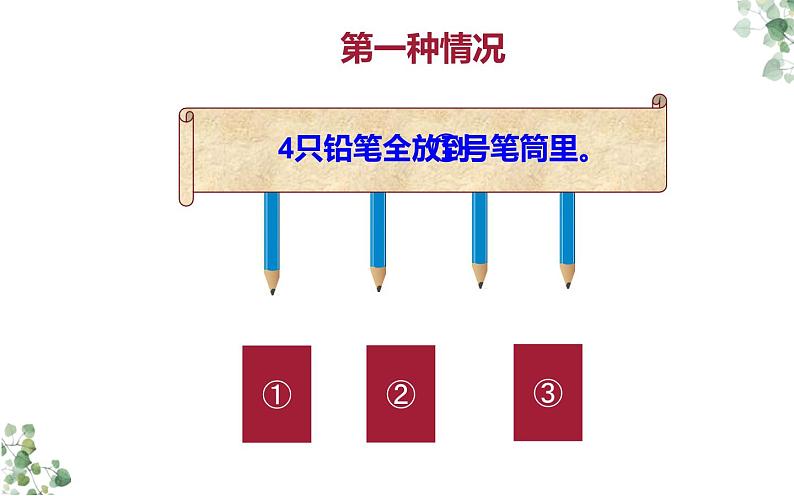
4只铅笔全放到①号笔筒里。
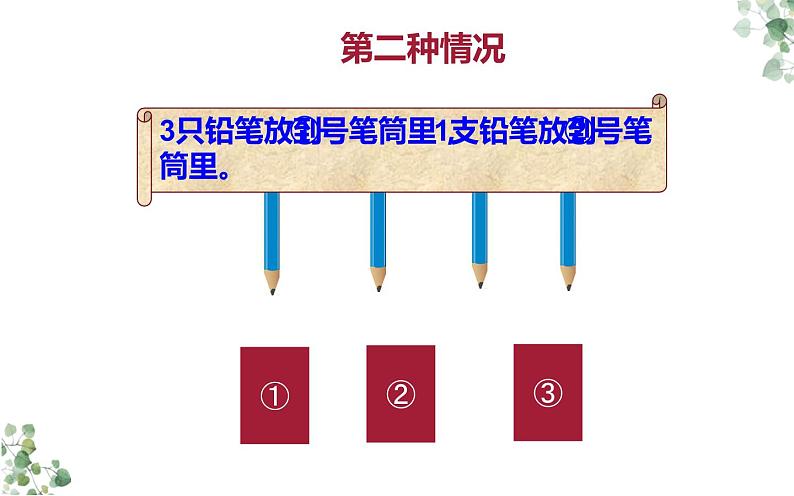
3只铅笔放到①号笔筒里，1支铅笔放到②号笔筒里。
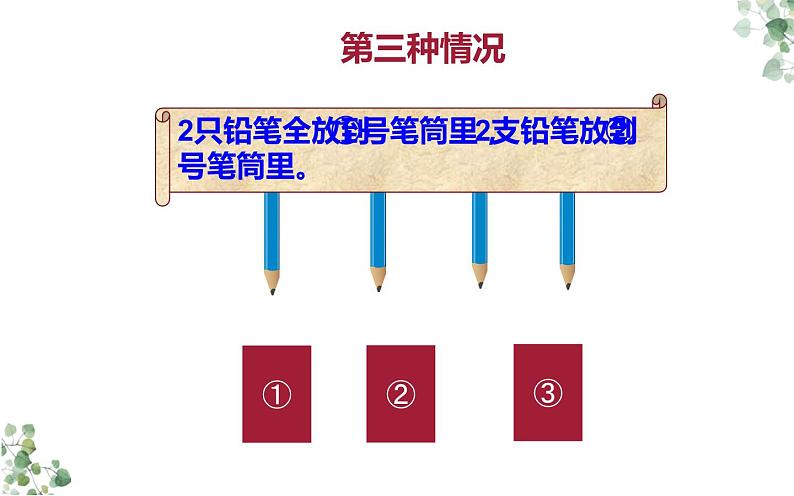
2只铅笔全放到①号笔筒里，2支铅笔放到②号笔筒里。
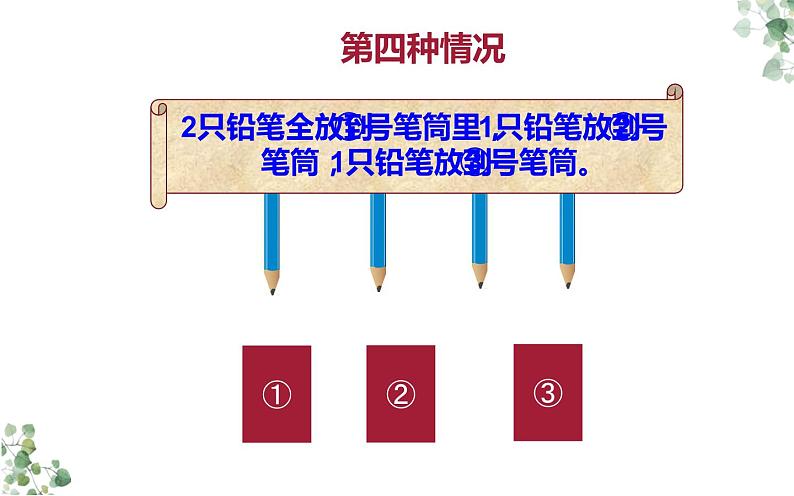
2只铅笔全放到①号笔筒里，1只铅笔放到②号笔筒，1只铅笔放到③号笔筒。
像这样把所有情况都列举出来的方法叫列举法。
请同学们观察不同的摆法，能发现什么？
不管怎么放，总有一个文具盒里至少放进2枝铅笔。
把4支笔平均放到3个盒子里
剩下的1支笔不管放到哪个文具盒，总有一个文具盒里至少有2枝铅笔。
像这样的方法叫做假设法。
把这4支铅笔放进这3个笔筒中,不管怎么放，总有一个笔筒里至少放进2支铅笔。
把6支铅笔放进5个笔筒里呢？
把7支铅笔放进6个笔筒里呢？
把100支铅笔放进99个笔筒里呢？
把n+1支铅笔放进n个笔筒里呢？
像这样的问题就是“鸽巢问题” ，也叫“抽屉问题”。它里面蕴含的数学原理，叫做“鸽巢原理”或“抽屉原理” 。
只要铅笔的支数比笔筒的数量多1，总有一个笔筒里至少有2支铅笔。
“鸽巢问题”最先是由19世纪的德国数学家狄利克雷提出来的，所以又称“狄利克雷原理”。“鸽巢问题” 的应用是千变万化的，用它可以解决许多有趣的问题，并且常常能得到一些令人惊异的结果。
狄利克雷（1805～1859）
为什么老师可以肯定地说：从52张牌中任意抽取5张牌，至少会有2张牌是同一花色的？你能用所学的抽屉原理来解释吗？
5÷4=1……1 1+1=2
如果4人选中了4种不同的花色，剩下的1人不管选，总会和其他4人中的一人相同，所以至少有2张牌是同一花色的。
5只鸽子飞进了4个鸽笼，总有一个鸽笼至少飞进了2只鸽子，为什么？
5 ÷ 4＝ 1（只） · · · · · ·1（只）
例2：把7本书放进3个抽屉中，不管怎么放，总有一个抽屉至少放进3本书？为什么？如果有8本书会怎么样呢？10本呢？
7÷3=2……1　　　2+1=3
把7本书平均放进3个抽屉里，每个抽屉里放2本书，剩下的1本书无论放进哪个抽屉里，总有1个抽屉里至少放了3本书。
如果有8本书会怎么样呢？
8÷3＝2……2 2+1=3
10÷3＝3……1 3+1=4
观察上面的式子你发现了什么规律吗？
物体数÷抽屉数=平均数┅┅余数
解决“鸽巢问题”关键是找准哪是物体，哪是抽屉。
解决“鸽巢问题”的关键是找准什么？
11只鸽子飞回4个鸽舍，至少有（ ）只鸽子要飞进同一个鸽舍。为什么？
1、11本书放进3个抽屉，至少有5本书要放进同一个抽屉里。 （ ）
2、17 只鸽子飞回5个鸽舍，至少有5个鸽子要飞进同一个鸽舍。 （ ）
1、5个人坐4把椅子，总有一把椅子上至少坐（ ）人。为什么？
2、实验小学六（1）班第一小组一共13位同学，一定至少有（ ）名同学的生日在同一个月。为什么？
5÷4=1 …… 1 1+1=2
13÷12=1 …… 1 1+1=2
3、张叔叔参加飞镖比赛，投了5镖，成绩是41环。张叔叔至少有一镖不低于（ ）环。为什么？
41÷5=8 …… 1 8+1=9
某学校有31名学生是6月份出生的，那么，其中至少有几名学生的生日是在同一天。
因为6月份有30天，相当于30个抽屉，31名学生相当于31个物体，31÷30=1……1，1+1=2，所以至少有2名学生的生日是同一天。