湘教版七年级下册第2章 整式的乘法综合与测试导学案及答案

这是一份湘教版七年级下册第2章 整式的乘法综合与测试导学案及答案，共13页。学案主要包含了学习目标，知识网络，要点梳理，典型例题，思路点拨，答案与解析，总结升华，巩固练习等内容，欢迎下载使用。

【学习目标】
1. 理解正整数幂的运算性质，并能运用它们熟练地进行运算；掌握单项式乘（或除以）单项式、多项式乘（或除以）单项式以及多项式乘多项式的法则，并运用它们进行运算；
2. 会推导乘法公式（平方差公式和完全平方公式），了解公式的几何意义，能利用公式进行乘法运算；
3. 掌握整式的加、减、乘、除、乘方的较简单的混合运算，并能灵活地运用运算律与乘法公式简化运算；
4. 理解因式分解的意义，并感受分解因式与整式乘法是相反方向的运算，掌握提公因式法和公式法（直接运用公式不超过两次）这两种分解因式的基本方法，了解因式分解的一般步骤；能够熟练地运用这些方法进行多项式的因式分解.
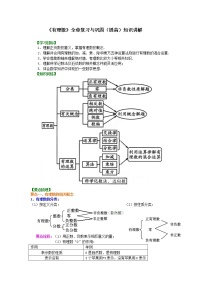
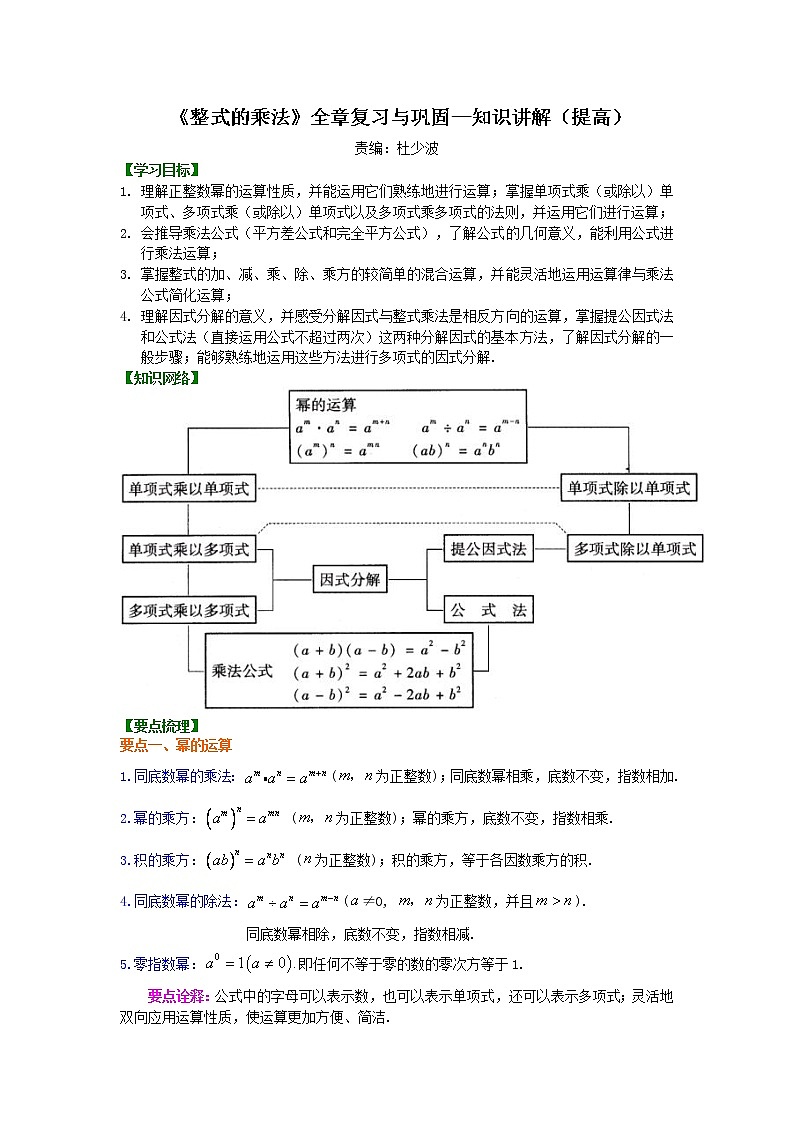
【知识网络】
【要点梳理】
要点一、幂的运算
1.同底数幂的乘法：(为正整数)；同底数幂相乘，底数不变，指数相加.
2.幂的乘方： (为正整数)；幂的乘方，底数不变，指数相乘.
3.积的乘方： (为正整数)；积的乘方，等于各因数乘方的积.
4.同底数幂的除法：(≠0, 为正整数，并且).
同底数幂相除，底数不变，指数相减.
5.零指数幂：即任何不等于零的数的零次方等于1.
要点诠释：公式中的字母可以表示数，也可以表示单项式，还可以表示多项式；灵活地双向应用运算性质，使运算更加方便、简洁.
要点二、整式的乘法和除法
1.单项式乘以单项式
单项式与单项式相乘，把他们的系数，相同字母分别相乘，对于只在一个单项式里含有的字母，则连同它的指数作为积的一个因式.
2.单项式乘以多项式
单项式与多项式相乘，就是用单项式去乘多项式的每一项，再把所得的积相加.即(都是单项式).
3.多项式乘以多项式
多项式与多项式相乘，先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加.即.
要点诠释：运算时，要注意积的符号，多项式中的每一项前面的“＋”“－”号是性质符号，单项式乘以多项式各项的结果，要用“＋”连结，最后写成省略加号的代数和的形式．根据多项式的乘法，能得出一个应用比较广泛的公式：.
4.单项式相除
把系数、相同字母的幂分别相除作为商的因式，对于只在被除式里出现的字母，则连同它的指数一起作为商的一个因式.
5.多项式除以单项式
先把这个多项式的每一项分别除以单项式，再把所得的商相加.
即：
要点三、乘法公式
1.平方差公式： 两个数的和与这两个数的差的积，等于这两个数的平方差.

要点诠释：在这里，既可以是具体数字，也可以是单项式或多项式.
平方差公式的典型特征：既有相同项，又有“相反项”，而结果是“相同项”的平方减去“相反项”的平方.
2. 完全平方公式：两数和 (差)的平方等于这两数的平方和加上（减去）这两数乘积的两倍.
；
要点诠释：公式特点：左边是两数的和（或差）的平方，右边是二次三项式，是这两数的平方和加（或减）这两数之积的2倍.
要点四、因式分解
把一个多项式化成几个整式的积的形式，像这样的式子变形叫做把这个多项式因式分解，也叫做把这个多项式分解因式.
因式分解的方法主要有: 提公因式法, 公式法等.
要点诠释：落实好方法的综合运用：
首先提取公因式，然后考虑用公式；
两项平方或立方，三项考虑完全平方；
四项以上想分组，分组分得要合适；
几种方法反复试，最后须是连乘式；
因式分解要彻底，一次一次又一次.
【典型例题】
类型一、幂的运算
1、已知，求的值．
【思路点拨】由于已知的值，所以逆用幂的乘方把变为，再代入计算．
【答案与解析】
解：∵，
∴．
【总结升华】本题培养了学生的整体思想和逆向思维能力．
举一反三：
【变式】（1）已知，比较的大小.
（2）比较大小。
【答案】
解：（1）； （2）
提示：（1）转化为同指数不同底数的情况进行比较，指数转化为12；
（2）转化成比较同底数不同指数，底数转化为3.
类型二、整式的乘除法运算
2、（2015•杭州模拟）已知代数式（mx2+2mx﹣1）（xm+3nx+2）化简以后是一个四次多项式，并且不含二次项，请分别求出m，n的值，并求出一次项系数．
【思路点拨】先把代数式按照多项式乘以多项式展开，因为化简后是一个四次多项式，所以x的最高指数m+2=4；不含二次项，即二次项的系数为0，即可解答．
【答案与解析】
解：（mx2+2mx﹣1）（xm+3nx+2）=mxm+2+3mnx3+2mx2+2mxm+1+6mnx2+4mx﹣xm﹣3nx﹣2，
因为该多项式是四次多项式，
所以m+2=4，
解得：m=2，
原式=2x4+（6n+4）x3+（3+12n）x2+（8﹣3n）x﹣2
∵多项式不含二次项，
∴3+12n=0，
解得：n=，
所以一次项系数8﹣3n=8+=．
【总结升华】本题考查了多项式乘以多项式，解决本题的关键是明确化简后是一个四次多项式，所以x的最高指数m+2=4；不含二次项，即二次项的系数为0，即可解答．
举一反三：
【变式】若的乘积中不含的一次项，则等于______．
【答案】；
类型三、乘法公式
3、计算：(1)；(2)．
【思路点拨】（1）中可以将两因式变成与的和差.（2）中可将两因式变成与的和差.
【答案与解析】
解：(1)原式
．
(2)原式

.
【总结升华】(1)在乘法计算中，经常同时应用平方差公式和完全平方公式．(2)当两个因式中的项非常接近时，有时通过拆项用平方差公式会达到意想不到的效果．
举一反三：
【变式】计算：．
【答案】
解：
．
4、已知，求代数式的值.
【思路点拨】将原式配方，变成几个非负数的和为零的形式，这样就能解出.
【答案与解析】
解：
所以
所以.
【总结升华】一个方程，三个未知数，从理论上不可能解出方程，尝试将原式配方过后就能得出正确答案.
举一反三：
【变式1】配方，求＝________.
【答案】
解：原式＝
所以，解得
所以.
【变式2】（2015春•祁阳县期末）课堂上老师指出：若a，b，c是△ABC的三边长，且满足a2+b2+c2﹣ab﹣bc﹣ac=0，请判断该三角形的形状．小明在与同学一起合作探究这个问题时，说出了自己的猜想及理由，得到了老师的赞扬．请你写出小明的猜想和理由．
【答案】
解：依题意得：
所以（a﹣b）2+（b﹣c）2+（c﹣a）2=0
所以a=b，b=c，c=a．
故△ABC是等边三角形．
5、求证：无论为何有理数，多项式的值恒为正数．
【答案与解析】
解：原式＝
所以多项式的值恒为正数.
【总结升华】通过配方，将原式变成非负数＋正数的形式，这样可以判断多项式的正负.
举一反三：
【变式】证明:不论为何值 , 多项式的值一定小于0.
【答案】
证明：
＝
＝
∵ ,
∴,
∴ 原式一定小于0.
类型四、因式分解
6、若，则E是（ ）
A． B． C． D．
【答案】C；
【解析】
解：．故选C．
【总结升华】观察等式的右边，提取的是，故可把变成，即左边＝.注意偶次幂时，交换被减数和减数的位置，值不变；奇次幂时，交换被减数和减数的位置，应加上负号．
举一反三：
【变式】把多项式提取公因式后，余下的部分是（ ）
A． B． C．2 D．
【答案】D；
解：，
＝，
＝．
7、分解因式：
（1）； （2）； （3）．
【思路点拨】（1）把看做整体，变形为后分解．（2）可写成，可写成，和分别相当于公式里的和．（3）把、看作一个整体进行分解．
【答案与解析】
解：（1）．
（2）
．
（3）
．
【总结升华】注意套用公式时要注意字母的广泛意义，可以是字母，也可以是单项式或多项式.
举一反三：
【变式】将下列各式分解因式：
（1）； （2）
（3）； （4）；
【答案】
解：（1）原式

（2）原式＝
＝
（3）原式
（4）原式
ADDIN CNKISM.UserStyle【巩固练习】
一.选择题
1．若二项式加上一个单项式后构成的三项式是一个完全平方式，则这样的单项式的个数有（ ）．
A．1个 B．2个 C．3个 D．4个
2. 已知：△ABC的三边长分别为，那么代数式的值（ ）
A.大于零 B.等于零 C.小于零 D不能确定
3. 下列因式分解正确的是( ).
A.B.
C. D.
4．（2015•邵阳）已知a+b=3，ab=2，则a2+b2的值为（ ）
A．3 B．4 C．5 D．6
5. 若能被60或70之间的两个整数所整除，这两个数应当是（ ）
A．61，63 B．61，65 C．63，65 D．63，67
6. 乘积应等于（ ）
A． B． C． D．
7. 下列各式中正确的有（ ）个：
①；② ； ③；
④；⑤；⑥
A. 1 B. 2 C. 3 D. 4
8. 若为任意实数时，二次三项式的值都不小于0，则常数满足的条件是（ ）
A. B. C. D.
二.填空题
9.（2015•游仙区模拟）已知关于x的二次三项式x2+2mx﹣m2+4是一个完全平方式，则m的值为 ．
10.若，，则用含的代数式表示为______．
11.已知，则＝ ．
12．若，化简＝_________．
13．若有一个因式为，则的值应当是_________.
14. 设实数，满足，则＝_________，＝__________.
15.已知，则＝ ．
16.分解因式：（1）＝________；（2）＝________.
三.解答题
17.（2015春•禅城区校级期末）请你说明：当n为自然数时，（n+7）2﹣（n﹣5）2能被24整除．
18.（2015春•碑林区期中）图①是一个长为2m，宽为2n的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后按图②的形状拼成一个正方形．
（1）图②中的阴影部分的面积为 ；
（2）观察图②，三个代数式（m+n）2，（m﹣n）2，mn之间的等量关系是 ；
（3）观察图③，你能得到怎样的代数等式呢？
（4）试画出一个几何图形，使它的面积能表示（m+n）（m+3n）；
（5）若x+y=﹣6，xy=2.75，求x﹣y的值．
19.计算
20.下面是某同学对多项式＋4进行因式分解的过程：
解：设
原式＝ （第一步）
＝ （第二步）
＝ （第三步）
＝ （第四步）
回答下列问题：
（1）该同学第二步到第三步运用了因式分解的（ ）
A．提取公因式 B.平方差公式
C.两数和的完全平方公式 D.两数差的完全平方公式
（2）该同学因式分解的结果是否彻底？______________(填彻底或不彻底)
若不彻底，请直接写出因式分解的最后结果_______________.
（3）请你模仿以上方法尝试对多项式 进行因式分解.
【答案与解析】
一.选择题
1. 【答案】D；
【解析】可以是，，.
2. 【答案】C；
【解析】，因为为三角形三边长，所以，所以原式小于零.
3. 【答案】C；
【解析】；
；
.
4. 【答案】C；
【解析】解：∵a+b=3，ab=2，
∴a2+b2
=（a+b）2﹣2ab
=32﹣2×2
=5，
故选C.
5. 【答案】C；
【解析】

6. 【答案】C；
【解析】

7. 【答案】D；
【解析】②④⑤⑥正确.
8. 【答案】B；
【解析】，由题意得，，所以.
二.填空题
9. 【答案】±；
【解析】解：∵关于x的二次三项式x2+2mx﹣m2+4是一个完全平方式，
即x2+2mx﹣m2+4，
∴﹣m2+4=m2，
解得：m=±．
故答案为：±．
10.【答案】
【解析】∵，∴.
11.【答案】－3；
【解析】.
12.【答案】
【解析】因为，所以，原式＝.
13.【答案】－6；
【解析】由题意，当时，，解得＝－6.
14.【答案】2；4；
【解析】等式两边同乘以4，得：
∴∴ .
15.【答案】39；
【解析】原式＝.
16.【答案】；；
【解析】；
.
三.解答题
17.【解析】
解：原式=（n+7+n﹣5）（n+7﹣n+5）
=24（n+1），
则当n为自然数时，（n+7）2﹣（n﹣5）2能被24整除．
18.【解析】
解：（1）阴影部分的边长为（m﹣n），所以阴影部分的面积为（m﹣n）2；
故答案为：（m﹣n）2；
（2）（m+n）2﹣（m﹣n）2=4mn；
故答案为：（m+n）2﹣（m﹣n）2=4mn；
（3）（m+n）（2m+n）=2m2+3mn+n2；
（4）答案不唯一：
（5）∵（x﹣y）2=（x+y）2﹣4xy=（﹣6）2﹣2.75×4=25，
∴x﹣y=±5．
19.【解析】
解：原式＝

.
20.【解析】
解：（1）C；
（2）不彻底；；
（3）设，原式＝
.