2022高考数学一轮复习专题45 空间几何体的折叠问题（解析卷）

这是一份2022高考数学一轮复习专题45 空间几何体的折叠问题（解析卷），共16页。试卷主要包含了题型选讲，折叠问题，折叠的综合性问题等内容，欢迎下载使用。
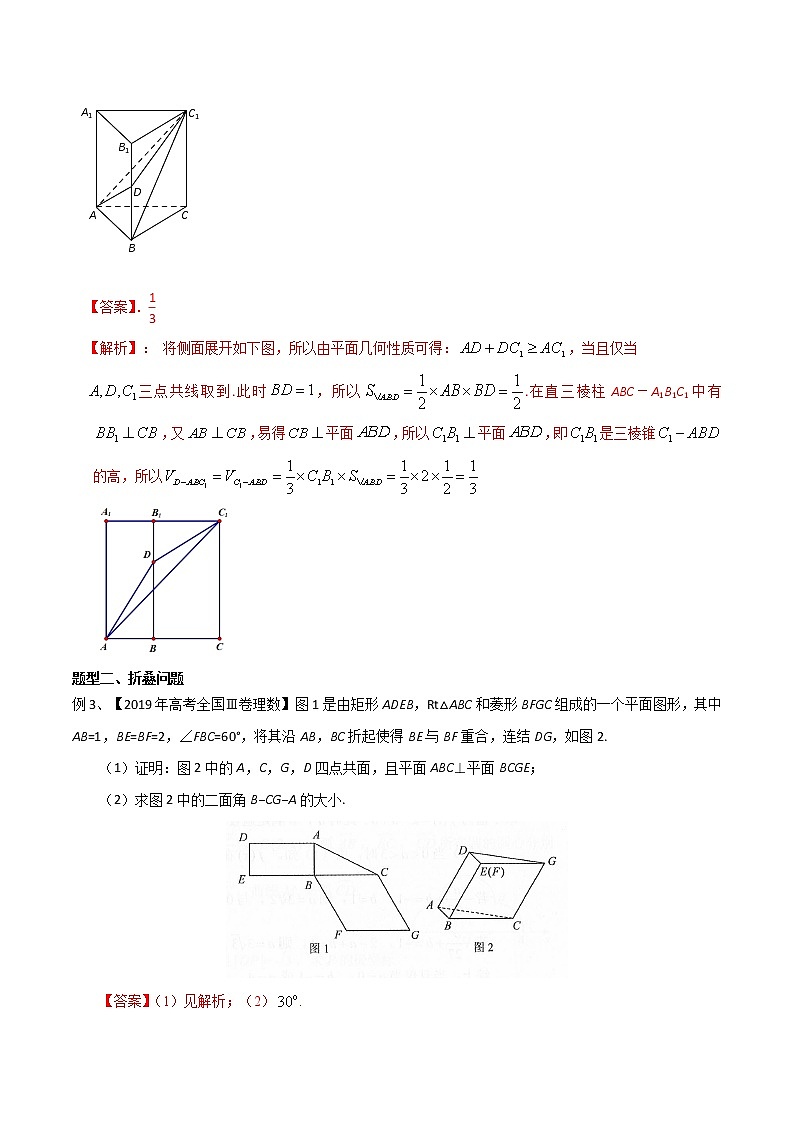
专题45  空间几何体的折叠问题一、题型选讲题型一 、展开问题例1、【2020年高考全国Ⅰ卷理数】如图，在三棱锥P–ABC的平面展开图中，AC=1，，AB⊥AC，AB⊥AD，∠CAE=30°，则cos∠FCB=______________.【答案】【解析】，，，由勾股定理得，同理得，，在中，，，，由余弦定理得，，在中，，，，由余弦定理得.故答案为：.例2、(2017南京三模）如图，在直三棱柱ABC－A1B1C1中，AB＝1，BC＝2，BB1＝3，∠ABC＝90°，点D为侧棱BB1上的动点．当AD＋DC1最小时，三棱锥D－ABC1的体积为   ▲   ．【答案】．  【解析】： 将侧面展开如下图，所以由平面几何性质可得：，当且仅当三点共线取到.此时，所以.在直三棱柱ABC－A1B1C1中有，又，易得平面，所以平面，即是三棱锥的高，所以题型二、折叠问题例3、【2019年高考全国Ⅲ卷理数】图1是由矩形ADEB，Rt△ABC和菱形BFGC组成的一个平面图形，其中AB=1，BE=BF=2，∠FBC=60°，将其沿AB，BC折起使得BE与BF重合，连结DG，如图2.（1）证明：图2中的A，C，G，D四点共面，且平面ABC⊥平面BCGE；（2）求图2中的二面角B−CG−A的大小.【答案】（1）见解析；（2）.【解析】（1）由已知得ADBE，CGBE，所以ADCG，故AD，CG确定一个平面，从而A，C，G，D四点共面．由已知得ABBE，ABBC，故AB平面BCGE．又因为AB平面ABC，所以平面ABC平面BCGE．（2）作EHBC，垂足为H．因为EH平面BCGE，平面BCGE平面ABC，所以EH平面ABC．由已知，菱形BCGE的边长为2，∠EBC=60°，可求得BH=1，EH=．以H为坐标原点，的方向为x轴的正方向，建立如图所示的空间直角坐标系H–xyz，则A（–1，1，0），C（1，0，0），G（2，0，），=（1，0，），=（2，–1，0）．设平面ACGD的法向量为n=（x，y，z），则即所以可取n=（3，6，–）．又平面BCGE的法向量可取为m=（0，1，0），所以．因此二面角B–CG–A的大小为30°．例4、【2018年高考全国Ⅰ卷理数】如图，四边形为正方形，分别为的中点，以为折痕把折起，使点到达点的位置，且.（1）证明：平面平面；（2）求与平面所成角的正弦值.【答案】（1）见解析；（2）.【解析】方法一：（1）由已知可得，BF⊥PF，BF⊥EF，所以BF⊥平面PEF.又平面ABFD，所以平面PEF⊥平面ABFD.（2）在平面DEF中，过P作PH⊥EF于点H，连接DH，如图，由于EF为平面ABCD和平面PEF的交线，PH⊥EF，则PH⊥平面ABFD，故PH⊥DH.则与平面所成的角为.在三棱锥P-DEF中，可以利用等体积法求PH.因为DE∥BF且PF⊥BF，所以PF⊥DE，又△PDF≌△CDF，所以∠FPD=∠FCD=90°，所以PF⊥PD，由于DE∩PD=D，则PF⊥平面PDE，故，因为BF∥DA且BF⊥平面PEF，所以DA⊥平面PEF，所以DE⊥EP.设正方形的边长为2a，则PD=2a，DE=a，在△PDE中，，所以，故，又，所以，所以在△PHD中，，故与平面所成角的正弦值为.方法二：（1）由已知可得，BF⊥PF，BF⊥EF，所以BF⊥平面PEF.又平面ABFD，所以平面PEF⊥平面ABFD.（2）作PH⊥EF，垂足为H.由（1）得，PH⊥平面ABFD.以H为坐标原点，的方向为y轴正方向，为单位长，建立如图所示的空间直角坐标系H−xyz.由（1）可得，DE⊥PE.又DP=2，DE=1，所以PE=.又PF=1，EF=2，故PE⊥PF.可得.则为平面ABFD的法向量.设DP与平面ABFD所成角为，则.所以DP与平面ABFD所成角的正弦值为.例5、（2020届山东省德州市高三上期末）如图（1），边长为的正方形中，，分别为、上的点，且，现沿把剪切、拼接成如图（2）的图形，再将，，沿，，折起，使、、三点重合于点，如图（3）.（1）求证：；（2）求二面角最小时的余弦值.【答案】（1）证明见解析；（2）.【解析】（1）折叠前，，折叠后，，又，所以平面，因此；（2）由（1）及题意知，因此以为原点，、、分别为、、轴建立空间直角坐标系如图：令，，，所以，，设平面法向量为则所以，令，则又平面法向量为，设二面角的大小为，所以，又，当且仅当取等号，所以.所以二面角最小时的余弦值为.例6、（2020届浙江省宁波市余姚中学高考模拟）如图，为正三角形，且，，将沿翻折.（1）若点的射影在上，求的长；（2）若点的射影在中，且直线与平面所成角的正弦值为，求的长.【答案】（1）2 （2）.【解析】（1）过A作交于E，则平面.取中点O，连接，，∵平面，平面，∴，又是正三角形，∴，又，AE，平面，∴平面，∴.又，O为的中点，∴为的中点.∵，∴，，，∴，.∴；（2）取中点为过点作平面的垂线，垂足为,连接,因为.以O为原点，以为x轴，以为y轴，以平面的过O的垂线为z轴建立空间直角坐标系，如图所示：设二面角为，因为平面，与（1）同理可证平面，，，则，，，.∴，，，设平面的法向量为，则，令，得.∴，解得.∴，又，∴.题型三、折叠的综合性问题例7、（2020届山东省滨州市高三上期末）已知菱形中，，与相交于点，将沿折起，使顶点至点，在折起的过程中，下列结论正确的是(     )A． B．存在一个位置，使为等边三角形C．与不可能垂直 D．直线与平面所成的角的最大值为【答案】ABD【解析】A选项，因为菱形中，与相交于点，所以，；将沿折起，使顶点至点，折起过程中，始终与垂直，因此，又，由线面垂直的判定定理，可得：平面，因此，故A正确；B选项，因为折起的过程中，边长度不变，因此；若为等边三角形，则；设菱形的边长为，因为，则，即，又，所以，即二面角的余弦值为时，为等边三角形；故B正确； C选项，，，由A选项知，，，所以，因此，同B选项，设菱形的边长为，易得，，所以，显然当时，，即；故C错误；D选项，同BC选项，设菱形的边长为，则，，，由几何体直观图可知，当平面，直线与平面所成的角最大，为，易知.故选：ABD.例8、（2020届浙江省台州市温岭中学3月模拟）如图，在直角梯形中，，，，为中点，，分别为，的中点，将沿折起，使点到，到，在翻折过程中，有下列命题：①的最小值为；②平面；③存在某个位置，使；④无论位于何位置，均有.其中正确命题的个数为（    ）A． B． C． D．【答案】D【解析】在直角梯形中，， ，，为中点，，分别为，的中点，将沿折起，使点到，到，在翻折过程中，当与重合时，的最小值为；所以①正确；连接交于连接，可以证明平面平面，所以平面，所以②正确；当平面时，可得平面，所以，所以③正确；因为，，所以直线平面，所以无论位于何位置，均有.所以④正确；故选：D. 二、达标训练1、（2020届山东省潍坊市高三上学期统考）已知边长为2的等边三角形，为的中点，以为折痕进行折叠，使折后的，则过，，，四点的球的表面积为（   ）A． B． C． D．【答案】C【解析】边长为2的等边三角形，为的中点，以为折痕进行折叠，使折后的，构成以D为顶点的三棱锥，且三条侧棱互相垂直，可构造以其为长宽高的长方体，其对角线即为球的直径，三条棱长分别为1,1，，所以，球面积，故选C.2、（2020届浙江省杭州市建人高复高三4月模拟）如图，点在正方体的表面上运动，且到直线与直线 的距离相等，如果将正方体在平面内展开，那么动点的轨迹在展开图中的形状是（ ） A． B．C． D．【答案】B【解析】在平面BCC1B1上，P到直线C1D1的距离为|PC1|，∵P到直线BC与直线C1D1的距离相等，∴点P到点C1的距离与到直线BC的距离相等，∴轨迹为抛物线,且点C1为焦点，BC为准线；故排除C，D，同理可得，在平面ABB1A1上，点P到点B的距离与到直线C1D1的距离相等，从而排除A，本题选择B选项.3、如图，在正方形ABCD中，E，F分别是BC，CD的中点，G是EF的中点，现在沿AE，AF及EF将这个正方形折成一个空间图形，使B，C，D三点重合，重合后的点记为H，则在这个空间图形中必有(　　)A. AG⊥平面EFH　　   B. AH⊥平面EFHC. HF⊥平面AEF　   D. HG⊥平面AEF【答案】 B【解析】 根据折叠，AH⊥HE，AH⊥HF不变，得AH⊥平面EFH，故B正确；因为过点A只有一条直线与平面EFH垂直，所以A不正确；因为AG⊥EF，EF⊥GH，AG∩GH＝G，所以EF⊥平面HAG，又EF⊂平面AEF，所以平面HAG⊥AEF，过点H作直线垂直于平面AEF，该直线一定在平面HAG内，所以C不正确；由条件证不出HG⊥平面AEF，所以D不正确．故选B.4、【2020年高考浙江】已知圆锥的侧面积（单位：cm2）为，且它的侧面展开图是一个半圆，则这个圆锥的底面半径（单位：cm）是_______．【答案】【解析】设圆锥底面半径为，母线长为，则，解得.故答案为：5、（2020届山东省济宁市高三上期末）下图是两个腰长均为的等腰直角三角形拼成的一个四边形，现将四边形沿折成直二面角，则三棱锥的外接球的体积为__________．【答案】【解析】由题设可将该三棱锥拓展成如图所示的正方体，则该正方体的外接球就是三棱锥的外接球，由于正方体的对角线长为，即球的半径，该球的体积，应填答案．6、(2018南京、盐城、连云港二模）在边长为4的正方形ABCD内剪去四个全等的等腰三角形(如图1中阴影部分)，折叠成底面边长为的正四棱锥SEFGH(如图2)，则正四棱锥SEFGH的体积为________．（图1）　　　　（图2）【答案】. 　【解析】：连结EG，HF，交点为O，正方形EFGH的对角线EG＝2，EO＝1，则点E到线段AB的距离为1，EB＝＝.SO＝＝＝2，故正四棱锥SEFGH的体积为×()2×2＝.7、【天津市和平区2020届高考三模】如图甲所示的平面五边形中，，，，，，现将图甲所示中的沿边折起，使平面平面得如图乙所示的四棱锥．在如图乙所示中
（1）求证：平面；（2）求二面角的大小；（3）在棱上是否存在点使得与平面所成的角的正弦值为？并说明理由．【答案】（1）证明见解析；（2）；（3）存在，理由见解析.【解析】（1）∵，，，∴，∴，∵平面平面，平面平面，∴平面，又∵平面，∴，又∵，，∴平面．（2）取的中点，连结，，由平面平面知平面，由知，以为坐标原点，所在的直线为轴，所在的直线为轴建立空间直角坐标系如图所示，则易得，，，，，设平面的法向量为，由，得，令得，，∴，设二面角大小为，则，∵，∴二面角的大小．（3）假设点存在，其坐标为，与平面所成的角为，则存在，有，即，，则，从而化简得，解得∵，∴∴在棱上满足题意的点存在．