人教版八年级下册第十八章 平行四边形综合与测试复习ppt课件

这是一份人教版八年级下册第十八章 平行四边形综合与测试复习ppt课件，共31页。PPT课件主要包含了概念性质判定，菱形常用的判定方法，正方形的性质，你会做吗，考考你等内容，欢迎下载使用。

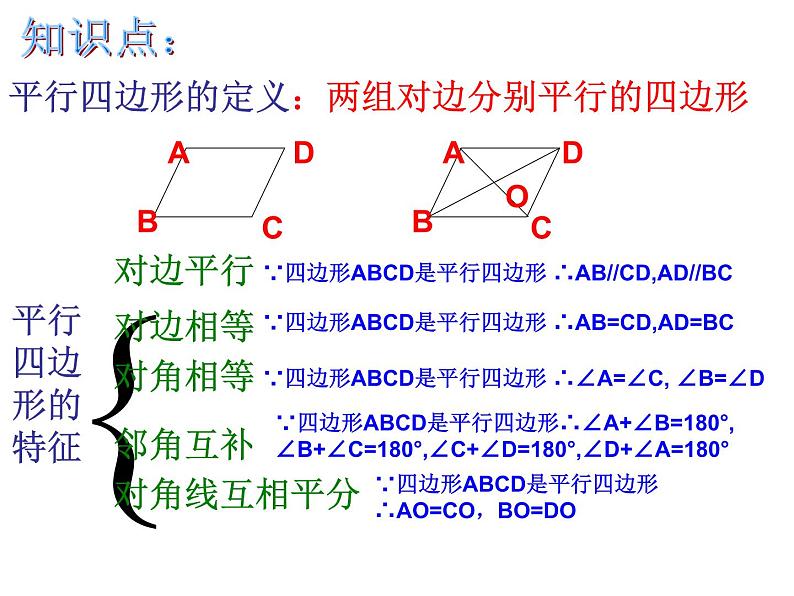
平行四边形的定义：两组对边分别平行的四边形
∵四边形ABCD是平行四边形 ∴AB//CD,AD//BC
∵四边形ABCD是平行四边形 ∴AB=CD,AD=BC
∵四边形ABCD是平行四边形 ∴∠A=∠C, ∠B=∠D
∵四边形ABCD是平行四边形∴∠A+∠B=180°,∠B+∠C=180°,∠C+∠D=180°,∠D+∠A=180°
∵四边形ABCD是平行四边形 ∴AO=CO，BO=DO
2.从角与角的关系:　
3.从对角线的相互关系:　
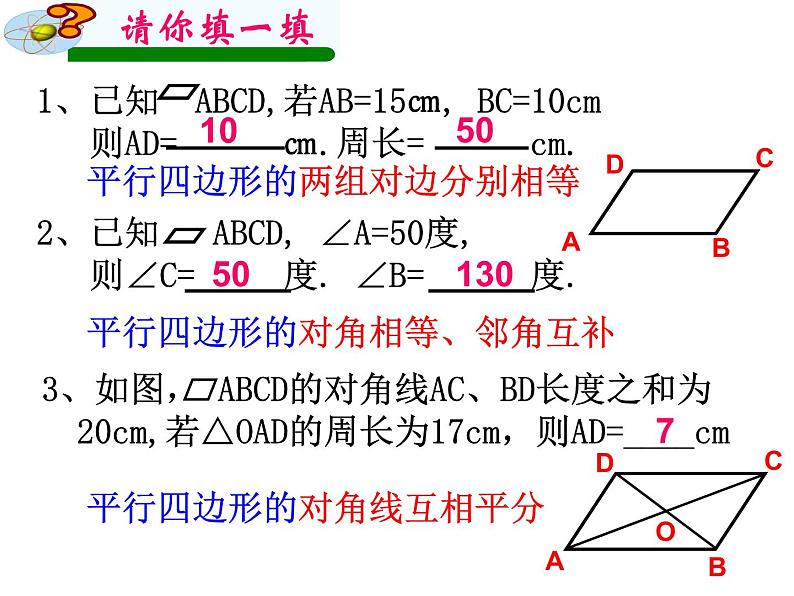
1、已知 ABCD,若AB=15㎝, BC=10cm 则AD= ㎝.周长= cm.
平行四边形的对角相等、邻角互补
平行四边形的两组对边分别相等
平行四边形的对角线互相平分
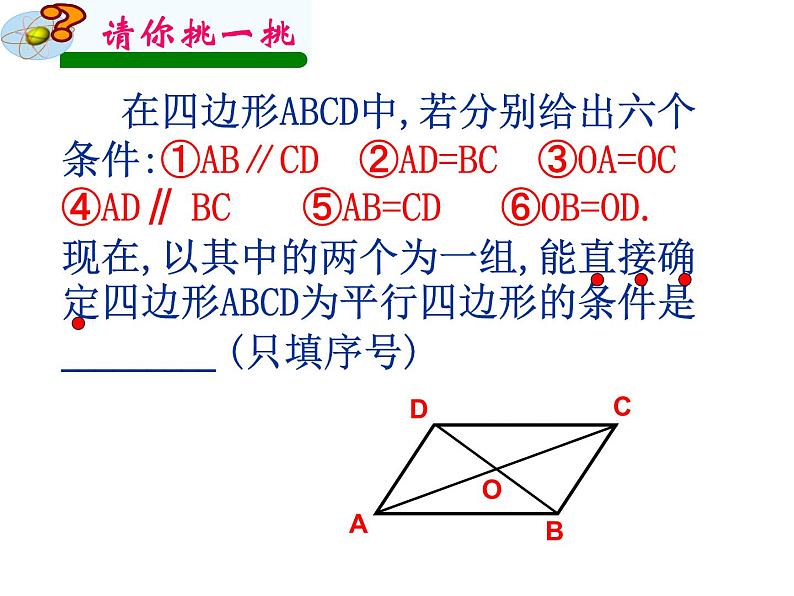
在四边形ABCD中,若分别给出六个条件:①AB∥CD ②AD=BC ③OA=OC ④AD∥ BC ⑤AB=CD ⑥OB=OD. 现在,以其中的两个为一组,能直接确定四边形ABCD为平行四边形的条件是 _________ (只填序号)
如图，在 ABCD中，E、F、G、H 分别是各边上的点，且AE=CF，BG=DH。求证：EF与GH互相平分。
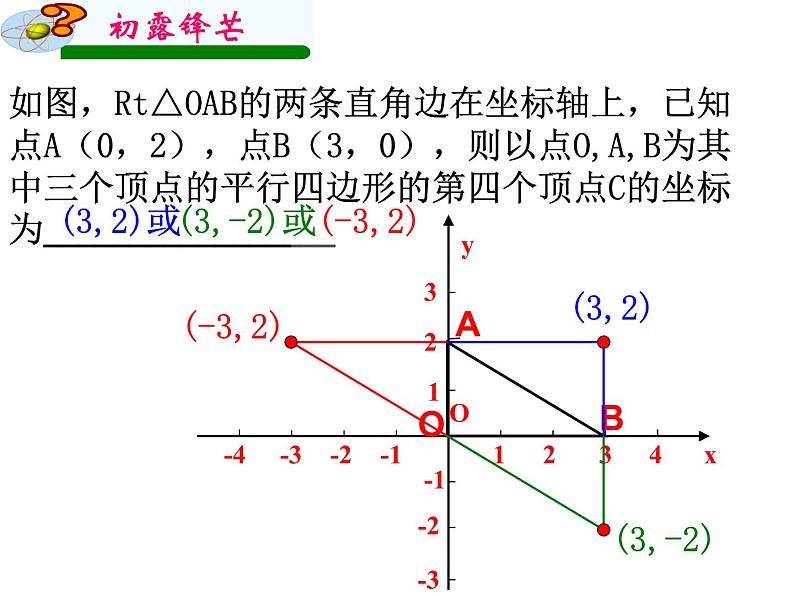
如图，Rt△OAB的两条直角边在坐标轴上，已知点A（0，2），点B（3，0），则以点O,A,B为其中三个顶点的平行四边形的第四个顶点C的坐标为_________________
矩形的四个角都是直角；
矩形的对角线相等且平分；
直角三角形斜边上的中线等于斜边的一半．
直角三角形斜边上中线的性质：
矩形的定义：有一个角是直角的平行四边形叫做矩形
有一个角是直角的平行四边形是矩形。
对角线相等的平行四边形是矩形 。
有三个角是直角的四边形是矩形 。
对角线相等且相互平分的四边形是矩形 。
1、如图，在矩形ABCD中，AC、BD相交于点O， ∠AOB= 60°，AB=6，则AC=_______
2、已知矩形的周长是24，相邻两边之比是1：2，那么这个矩形的面积是_____________
3、矩形的两条对角线的夹角为60°，一条对角线与短边的和为15，则短边长为____________
4、请在横线上写出原因，在括号里填理由 ∵四边形ABCD是矩形 ∴____________________ ( )
5、矩形具有而一般的平行四边形不具有的性质是(　　　) A、对角相等 B、对边相等 C、对角线相等 D、对角线互相平分
6、把一张长方形的纸条按图那样折叠，若得到∠AME＝70 ，则∠EMN＝（ ） A、45 B、50 C、55 D、60
7、如图，矩形ABCD沿AE折叠，使D点落在BC边上的F点处，如果∠BAF=60°，那么∠DAE等于（ ） A．15°B．30° C．45° D．60°
有一组邻边相等的平行四边形叫做菱形。
对角线互相平分、互相垂直且平分每一组对角
有一组邻边相等的平行四边形是菱形.
对角线互相垂直的平行四边形是菱形.
有四条边相等的四边形是菱形.
对角线互相垂直且平分的四边形是菱形.
1、如图，在菱形ABCD中，AB=10，OA=8，OB=6，则菱形的周长是_________，面积是___________
2、如图，在菱形ABCD中， ∠B= 120°，则∠DAC=___________
3、菱形的一个内角为120°，较短的对角线长为10，那么菱形的周长是_____________
每条对角线平分一组对角
正方形具有平行四边形、矩形、菱 形的一切性质。
判断四边形是正方形有哪些方法？
2、先说明它是矩形，再说明这个矩形有一组邻边相等．
3、先说明它是菱形，再说明这个菱形有一个角是直角．
1、先说明它是平行四边形，再说明有一组邻边相等，有一个角是直角。(定义法）
几种平行四边形的特征比较
对边平行,四条边都相等
对角线互相垂直平分,每条对角线平分对角
对角线互相垂直平分且相等,每条对角线平分对角
要使矩形ABCD成为正方形，需增加的条件是____
要使菱形ABCD成为正方形，需增加的条件是____
要使四边形ABCD成为正方形，需增加的条件是____
1、矩形具有而一般的平行四边形不具有的性质是(　) A、对角相等 B、对角线相等 C、对边相等 D、对角线互相平分2、菱形有而一般的平行四边形不具有的性质是(　) A、对角相等 B、对角线互相平分 C、对边平行且相等 D、对角线互相垂直
(3).下列性质中，平行四边形不一定具备的是（ ）
(A)对角相等 (B)邻角互补(C )对角互补 (D)内角和是360°
(A)一组对边平行，另一组对边也平行；(B)一组对角相等，另一组对角也相等；
(4).下面判定四边形是平行四边形的方法中， 错误的是（ ）。
(C )一组对边平行，一组对角相等； (D)一组对边平行，另一组对边相等
5.如图，在四边形ABCD中，E、F、G、H分别是边AB、BC、CD、DA的中点，请添加一个条件，使四边形EFGH为菱形，并说明理由。 解：添加的条件__________
三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半.
例5.顺次连接任意四边形各边的中点，所构成的四边形以下简称为“中点四边形”。试判断中点四边形EFGH的形状，并说明理由。
（1）添加一个条件，使四边形EFGH为菱形；
AC=BD且AC ⊥ BD
（2）添加一个条件，使四边形EFGH为矩形；
（3）添加一个条件，使四边形EFGH为正方形；
顺次连接任意的四边形各边中点得顺次连接对角线相等的四边形各边中点得顺次连接对角线互相垂直的四边形各边中点得顺次连接对角线相等且互相垂直的四边形各边中点得
1.矩形的“中点四边形”是 形；2.菱形的“中点四边形”是 形3.正方形的“中点四边形”是 形。
那么，特殊平行四边形的“中点四边形”会是怎样的图形呢？
1、检查一个门框是矩形的方法是（ ） A、测量两条对角线是否相等. B、测量有三个角是直角. C、 测量两条对角线是否互相平分. D、 测量两条对角线是否互相垂直.2、顺次连接矩形各边中点所得的四边形是（ ） A、矩形 B、菱形 C、梯形 D、正方形
3、菱形的周长等于高的8倍，则其最大内角 等于（ ） A、60° B、90° C、120° D、150° 4、矩形ABCD中，AB=8，BC=6，E、F是AC的三等分点，则△BEF的面积是（ ）A、8 B、12 C、16 D、24
5、在正方形ABCD中，E在BC上，BE=2，CE=1，P在BD上，则PE和PC的长度之和最小可达到_____________
在矩形ABCD中，AB=16，BC=8.将矩形沿AC折叠，点D落在点E处，且CE交AB于点F，求AF的长.
点拨：对于折叠问题，可以从折叠前后的两个图形是全等图形入手进行分析.