课时训练22 锐角三角函数
展开课时训练(二十二) 锐角三角函数
(限时:20分钟)
|夯实基础|
1.[2017·天津] cos60°的值等于 ( )
A. B.1 C. D.
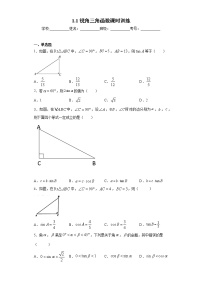
2.[2017·湖州] 如图K22-1,已知在Rt△ABC中,∠C=90°,AB=5,BC=3,则cosB的值是 ( )
图K22-1
A. B. C. D.
3.[2018·益阳] 如图K22-2,小刚从山脚A出发,沿坡角为α的山坡向上走了300米到达B点,则小刚上升了 ( )
图K22-2
A.300sinα米 B.300cosα米
C.300tanα米 D.米
4.[2018·常州] 某数学研究性学习小组制作了如图K22-3的三角函数计算图尺:在半径为1的半圆形量角器中,画一个直径为1的圆,把刻度尺CA的0刻度固定在半圆的圆心O处,刻度尺可以绕点O转,从图中所示的图尺可读出sin∠AOB的值是 ( )
图K22-3
A. B. C. D.
5.[2018·日照] 如图K22-4,边长为1的小正方形构成的网格中,半径为1的☉O的圆心O在格点上,则∠BED的正切值等于 ( )
图K22-4
A. B. C.2 D.
6.[2018·荆州] 如图K22-5,平面直角坐标系中,☉P经过三点A(8,0),O(0,0),B(0,6),点D是☉P上的一动点,当点D到弦OB的距离最大时,tan∠BOD的值是 ( )
图K22-5
A.2 B.3 C.4 D.5
7.[2018·天水] 已知在Rt△ABC中,∠C=90°,sinA=,则tanB的值为 .
8.如图K22-6,点A(3,t)在第一象限,射线OA与x轴所夹的锐角为α,tanα=,则t的值是 .
图K22-6
9.[2018·枣庄] 如图K22-7,某商店营业大厅自动扶梯AB的倾斜角为31°,AB的长为12米,则大厅两层之间的高度约为 米.(结果精确到0.1米)
【参考数据:sin31°≈0.515,cos31°≈0.857,tan31°≈0.601】
图K22-7
10.如图K22-8,在半径为3的☉O中,直径AB与弦CD相交于点E,连接AC,BD,若AC=2,则tanD= .
图K22-8
11.计算:(1)+-1-(3-π)0-;
(2)6tan230°-sin60°-2sin45°.
12.如图K22-9,在△ABC中,∠ABC=90°,∠A=30°,D是边AB上一点,∠BDC=45°,AD=4.求BC的长(结果保留根号).
图K22-9
13.如图K22-10,AD是△ABC的中线,tanB=,cosC=,AC=.求:
(1)BC的长;
(2)sin∠ADC的值.
图K22-10
14.如图K22-11,在Rt△ABC中,∠ACB=90°,AC=BC=3,点D在边AC上,且AD=2CD,DE⊥AB,垂足为点E,连接CE,求:
(1)线段BE的长;
(2)∠ECB的正切值.
图K22-11
|拓展提升|
15.[2017·福建] 小明在某次作业中得到如下结果:
sin27°+sin283°≈0.122+0.992=0.9945,
sin222°+sin268°≈0.372+0.932=1.0018,
sin229°+sin261°≈0.482+0.872=0.9873,
sin237°+sin253°≈0.602+0.802=1.0000,
sin245°+sin245°=2+2=1.
据此,小明猜想:对于任意锐角α,均有sin2α+sin2(90°-α)=1.
(1)当α=30°时,验证sin2α+sin2(90°-α)=1是否成立;
(2)小明的猜想是否成立?若成立,请给予证明;若不成立,请举出一个反例.
参考答案
1.D
2.A [解析] 在Rt△ABC中,cosB==.
3.A [解析] ∵sinα=,∴BO=ABsinα=300sinα米,故选择A.
4.D [解析] 如图,连接EF,由题意可知OF=0.8,OE=1,
∵∠OEF+∠EOF=∠EOF+∠BOF,∴∠OEF=∠AOB,
∵OE是直径,∴∠EFO=90°,
∴sin∠AOB==,故选D.
5.D [解析] 如图,在Rt△ABC中,AB=2,BC=1,
∴tan∠BAC==.
∵∠BED=∠BAD,
∴tan∠BED=.故选D.
6.B [解析] 如图所示,当点D到弦OB的距离最大时,DE⊥OB于E点,且D,E,P三点共线.连接AB,由题意可知AB为☉P的直径,∵A(8,0),∴OA=8,∵B(0,6),∴OB=6,∴OE=BE=OB=3,在Rt△AOB中,AB==10,∴BP=AB=×10=5,在Rt△PEB中,PE==4,∴DE=EP+DP=4+5=9,∴tan∠DOB===3,故选B.
7. [解析] 在Rt△ABC中,sinA=,令BC=a=12k,AB=c=13k,
根据勾股定理,得AC=b=5k.
∴tanB==.
8. [解析] 作AB⊥x轴于B,
∵点A(3,t)在第一象限,
∴AB=t,OB=3,又∵tanα==,∴t=.
9.6.2 [解析] 运用锐角三角函数:=sin∠BAC,即=sin31°,BC≈12×0.515=6.18≈6.2(米),故填6.2.
10.2 [解析] 如图,连接BC,
∵AB是☉O的直径,∴∠ACB=90°,
∵AB=6,AC=2,
∴BC===4,
又∵∠D=∠A,
∴tanD=tanA===2.
故答案为2.
11.解:(1)原式=2+2-1-
=2+2-1+1-
=+2.
(2)原式=6×2-×-2×=-.
12.解:∵∠ABC=90°,∠BDC=45°,∴BD=BC.
∵∠ABC=90°,∠A=30°,
∴AB=BC,∴AD+BD=BC,
即AD+BC=BC.
∵AD=4,∴4+BC=BC,
解得BC=2+2.
13.[解析] (1)过点A作AE⊥BC于点E,根据cosC=,求出∠C=45°,求出AE=CE=1,根据tanB=,求出BE,进而求出BC;
(2)根据AD是△ABC的中线,求出CD的长,得到DE的长,进而得出∠ADC的度数,求出正弦值.
解:(1)如图,过点A作AE⊥BC于点E,
∵cosC=,∴∠C=45°,
在Rt△ACE中,CE=AC·cosC=1,
∴AE=CE=1,
在Rt△ABE中,tanB=,
即=,∴BE=3AE=3,
∴BC=BE+CE=4.
(2)∵AD是△ABC的中线,∴CD=BC=2,
∴DE=CD-CE=1,
∵AE⊥BC,DE=AE,∴∠ADC=45°,
∴sin∠ADC=.
14.解:(1)∵AD=2CD,AC=3,∴AD=2,
∵在Rt△ABC中,∠ACB=90°,AC=BC=3,
∴∠A=∠B=45°,AB===3,
∵DE⊥AB,∴∠AED=90°,
∴AE=AD·cos45°=2×=,
∴BE=AB-AE=3-=2,
即线段BE的长为2.
(2)过点E作EH⊥BC,垂足为点H,如图所示.
∵在Rt△BEH中,∠EHB=90°,∠B=45°,
∴EH=BH=BE·cos45°=2×=2,∵BC=3,∴CH=1,
在Rt△CHE中,tan∠ECB==2,
即∠ECB的正切值为2.
15.解:(1)当α=30°时,sin2α+sin2(90°-α)=sin230°+sin260°=2+2=+=1.
所以sin2α+sin2(90°-α)=1成立.
(2)小明的猜想成立.证明如下:
如图,在△ABC中,∠C=90°,
设∠A=α,则∠B=90°-α.
sin2α+sin2(90°-α)=2+2===1.
数学九年级下册28.1 锐角三角函数精练: 这是一份数学九年级下册28.1 锐角三角函数精练,共5页。试卷主要包含了选择题,填空题等内容,欢迎下载使用。
初中数学沪科版九年级上册23.1 锐角的三角函数同步训练题: 这是一份初中数学沪科版九年级上册23.1 锐角的三角函数同步训练题,文件包含231锐角三角函数原卷版doc、231锐角三角函数解析版doc等2份试卷配套教学资源,其中试卷共13页, 欢迎下载使用。
初中数学苏科版九年级下册第7章 锐角函数7.6 用锐角三角函数解决问题同步达标检测题: 这是一份初中数学苏科版九年级下册第7章 锐角函数7.6 用锐角三角函数解决问题同步达标检测题,共11页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。