人教版第十七章 勾股定理17.2 勾股定理的逆定理完美版ppt课件

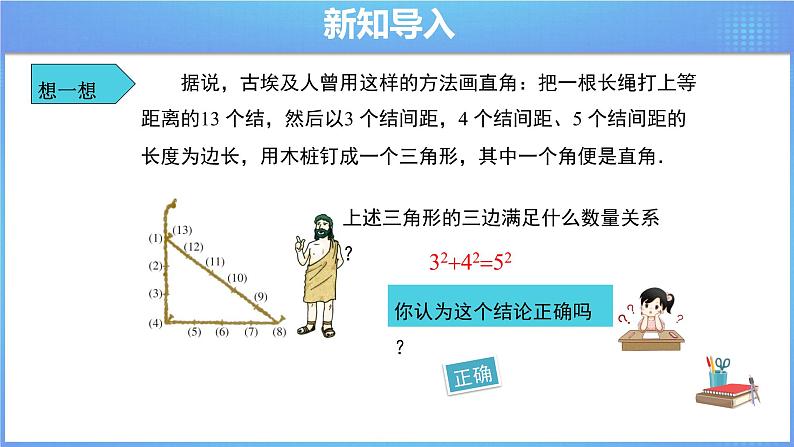
导入新课

【复习回顾】

1.直角三角形有哪些性质?

预设答案：(1)有一个角是直角；(2)两个锐角互余；(3)两直角边的平方和等于斜边的平方；(4)在含30°角的直角三角形中，30°的角所对的直角边是斜边的一半.

2.一个三角形，满足什么条件是直角三角形?

预设答案：(1)有一个角是直角；(2)有两个角的和是90°.

教师活动：教师提出问题，引导学生回顾直角三角形的性质，以及如何判断一个三角形是直角三角形.全班学生回答.然后教师让学生观察第2问的结果，引导学生发现，目前的两种方法都是从角度出发判断一个三角形是不是直角三角形的.进一步追问：能用三角形三边的关系来判断是否为直角三角形吗？

【想一想】

据说，古埃及人曾用这样的方法画直角：把一根长绳打上等距离的13 个结，然后以3 个结间距，4 个结间距、5 个结间距的长度为边长，用木桩钉成一个三角形，其中一个角便是直角．

上述三角形的三边满足什么数量关系？

预设答案：324252

你认为这个结论正确吗？

预设答案：正确

学生回顾并根据老师的提问进行思考,并回答.

学生测量课本中三角形的角度，并计算三边长的关系.形

通过对前面所学知识的归纳总结，联想到用三边的关系是否可以判断一个三角形为直角三角形，引导学生自然合理地提出问题.

介绍前人经验，启发思考，使学生意识到数学知识来源于生活实际，激发学习兴趣.

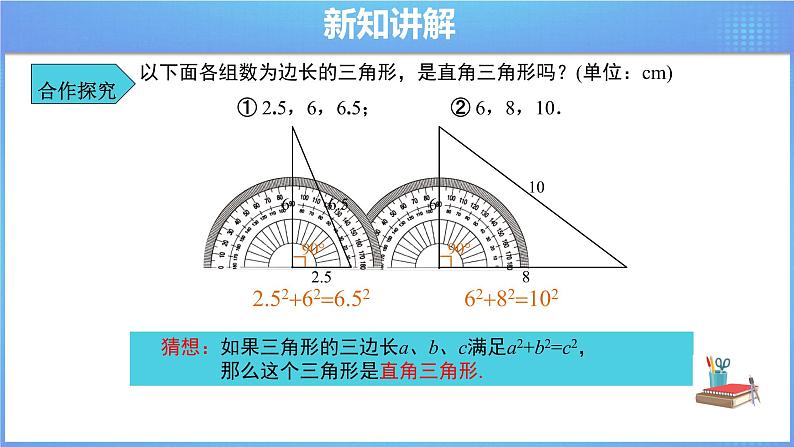
讲授新课

【合作探究】

以下面各组数为边长的三角形，是直角三角形吗？(单位：cm)

① 2.5，6，6.5；  ② 6，8，10．      

【操作】

1.画一画：分别以这些数为三边长画出三角形；

2.算一算：每组中较小两个数的平方和与较大数的平方之间有什么关系？

3.量一量：用量角器分别测量三角形中最大角的度数；

4.想一想：试着判断这些三角形的形状，并提出猜想.

教师活动：教师指导学生按要求画出三角形，并计算三边的数量关系，2.52626.52，6282102. 接着度量三角形最大角的度数，发现最大角为90°.教师引导学生提出猜想：

     如果三角形的三边长a、b、c满足a2+b2=c2，那么这个三角形是直角三角形.

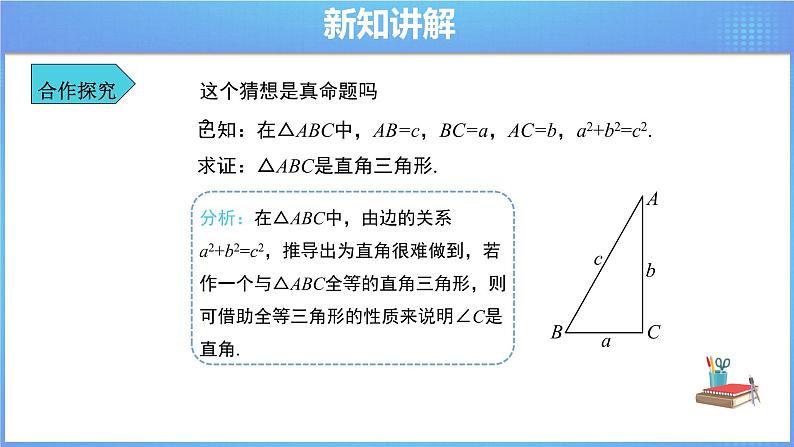
追问：这个命题是真命题吗？

教师活动：要证明一个命题是真命题，首先要分析命题的题设和结论，画出图形，写出已知、求证.教师让学生自行完成.

已知：在△ABC中，AB=c，BC=a，AC=b，a2+b2=c2.

求证：△ABC是直角三角形.

追问：要证明△ABC是直角三角形，只需要证明∠C是直角即可，由已知条件，能直接证明吗?

教师活动：引导学生发现在△ABC中，由边的关系a2+b2=c2，推导出为直角很难做到，若作一个与△ABC全等的直角三角形，则可借助全等的性质来说明∠C是直角.

【证明猜想】

已知：在△ABC中，AB=c，BC=a，AC=b，a2+b2=c2.

求证：△ABC是直角三角形.

证明：如图，作△A'B'C'，使∠C'=90°，B'C'=a，A'C'=b.

由勾股定理可得A'B'2=a2+b2.

∵a2+b2=c2，∴A'B'2=c2.

在△ABC和△A'B'C'中，

∵AB=A'B'=c，BC=B'C'=a，AC=A'C'=b.

∴△ABC≌△A'B'C'(SSS).

∴∠C'=∠C=90°(全等三角形的对应角相等).

即△ABC是直角三角形.

教师活动：引导学生分析，通过构造一个直角三角形，利用同一法证明△ABC为直角三角形.

所以命题2是真命题，也是一个定理，可以用这个定理判定一个三角形是否为直角三角形.

【小试牛刀】

下面以a，b，c为边长的三角形是不是直角三角形？

(1) a5，b12，c13；

(2) a6，b7，c8；

(3) a1，b2，c.

答：(1) 52+122132，是直角三角形.

(2) 62+7282，不是直角三角形.

(3) 12+()222，是直角三角形.

教师活动：先由学生独立完成，教师及时给予指导，在此活动中，教师应重点关注学生能否进一步理解勾股定理的逆定理的用处，以及能否用几何语言规范地书写过程，并介绍勾股数

像5，12，13这样能够成为直角三角形三条边长的三个正整数，称为勾股数.

【合作探究】

与上节课学习的命题1比较，命题1、命题2的题设、结论分别是什么？

命题1  如果直角三角形的两条直角边长分别为a，b，斜边长为c，那么a2+b2=c2.

命题2  如果三角形的三边长a、b、c满足a2+b2=c2，那么这个三角形是直角三角形.

教师活动：教师带领学生分析两个命题的题设和结论，并让学生初步感受两个命题的题设和结论的关系，然后教师介绍原命题、逆命题、互逆命题等概念.

命题1与命题2的题设、结论正好相反. 我们把像这样的两个命题叫做互逆命题.

如果我们把其中一个叫做原命题，那么另一个叫做它的逆命题.

如：把命题1叫做原命题，那么命题2就是命题1的逆命题.

教师活动：教师引导学生回顾，上节课我们已经学过了命题1，知道它是真命题，通过刚刚的证明我们也知道命题2也是真命题.教师引导学生思考，原命题成立时，它的逆命题一定成立吗？让学生思考，小组讨论交流，教师汇总，并补充.

     预设答案：

     (1)原命题：如果两个角是对顶角，那么这两个角相等. 真命题.

逆命题：如果两个角相等，那么这两个角是对顶角.假命题.

     (2)原命题：如果两直线平行，那么同位角相等.真命题.

逆命题：如果同位角相等，那么两直线平行.真命题.

    结论：原命题成立时，它的逆命题可能成立，也可能不成立.

    一般地，如果一个定理的逆命题经过证明是正确的，那么它也是一个定理，称这两个定理互为逆定理.

    如：命题1是上节课学习的勾股定理，命题2叫做勾股定理的逆定理.命题1与命题2不仅是互逆命题，还是互逆定理.

学生按要求画图、计算、测量、猜想.

学生计算并回答

学生思考并举例说明.

教学中先要求学生画几个三角形，测量边长，然后计算边长的平方，并分析最长边的平方与其他两边平方和之间的关系，最后引导得出结论，这种测量、计算、归纳和猜想的过程，是典型的几何探索过程.

本问题中，难以直接证明△ABC是直角三角形，联想到三角形全等这一工具，通过构造直角三角形，证明当前三角形与一个直角三角形全等，从而证明当前三角形是直角三角形.让学生体会这种证明思路的合理性，帮助学生突破难点.

通过练习，把陈述性的定理转化为认知操作，学会用勾股定理及其逆定理判断一个三角形是否为直角三角形.

以PK的形式让学生进一步熟悉在数轴上表示无理数的点的步骤，提高学习积极性.

通过归纳总结让学生熟悉利用勾股定理在数轴上表示无理数的方法，培养归纳概括能力和应用意识.

    通过分析命题1与命题2的题设和结论之间的关系，使学生了解原命题、逆命题、互逆命题、互逆定理的概念.

【典型例题】

教师提出问题，学生先独立思考，解答.然后再小组交流探讨，教师巡视，如遇到有困难的学生适当点拨，最终教师展示答题过程.

例 判断由a、b、c组成的三角形是不是直角三角形：

(1) a15，b8，c17；(2) a13，b14，c15.

分析：由勾股定理的逆定理，判断三角形是不是直角三角形，只要看两条较小边的平方和是否等于最大边的平方.

解：(1)∵1528222564289

                  172289

  ∴15282172

  ∴根据勾股定理的逆定理，这个三角形是直角三角形.

(2)∵132142169196365

                152225

  ∴132142152

  ∴根据勾股定理，这个三角形不是直角三角形.

【课堂练习】

 教师给出练习，随时观察学生完成情况并相应指导，最后给出答案，根据学生完成情况适当分析讲解.

1.△ABC中A， B， C的对边分别是a，b，c，则下列命题中的假命题是(      )

A.如果CBA，则△ABC是直角三角形；

B.如果c2=b2a2，则△ABC是直角三角形，且C90°；

C.如果(ca)(ca)=b2，则△ABC是直角三角形；

D.如果A  B  C=5  2  3，则△ABC是直角三角形.

答：B.

2.下列四组线段，不能构成直角三角形的是(   )

A. a8，b15，c17；

B. a9，b12，c15；

C. a，b，c；

D. a  b  c2  3  4.

答：D.

3.写出下列命题的逆命题，并判断逆命题是否成立.

 (1)全等三角形的对应角相等.

 (2)两直线平行，内错角相等.

 (3)互为相反数的两个数的绝对值相等.

解：(1)对应角相等的两个三角形是全等三角形；不成立.

(2)内错角相等，两直线平行；成立.

(3)绝对值相等的两个数互为相反数. 不成立.

学生思考、计算并回答.

自主完成练习，然后集体交流评价.

巩固所学知识，加深对勾股定理的逆定理的理解.

通过课堂练习及时巩固本节课所学内容，并考查学生的知识应用能力，培养独立完成练习的习惯.

课堂小结

以思维导图的形式呈现本节主要内容：

回顾本节课所讲的内容

通过小结让学生进一步熟悉巩固本节课所学的知识.

板书

1.勾股定理的逆定理

如果三角形的三边长a、b、c满足a2+b2=c2，那么这个三角形是直角三角形.

2.互逆命题

（1）原命题     （2）逆命题

3.例题讲解