专题01 角平分线的五种模型--中考数学必备几何模型讲义（全国通用）

这是一份专题01 角平分线的五种模型--中考数学必备几何模型讲义（全国通用），文件包含专题01角平分线的五种模型讲义+练习老师版docx、专题01角平分线的五种模型讲义+练习学生版docx等2份试卷配套教学资源，其中试卷共25页， 欢迎下载使用。
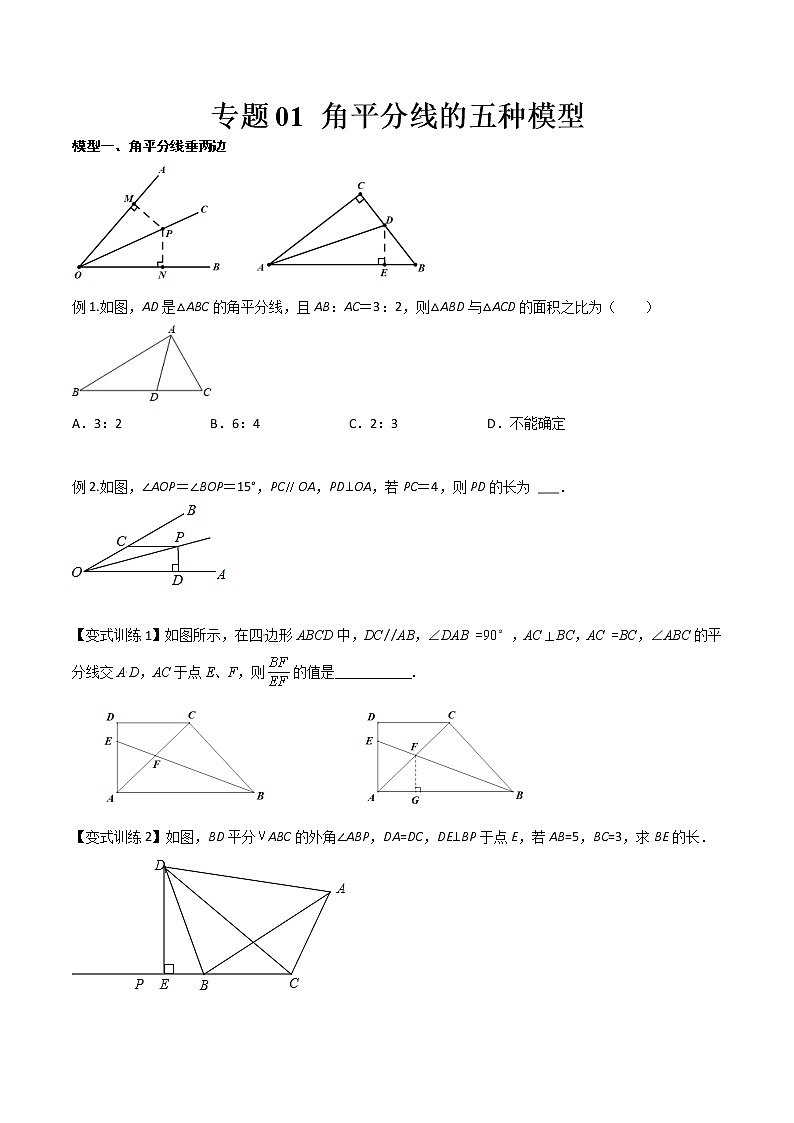
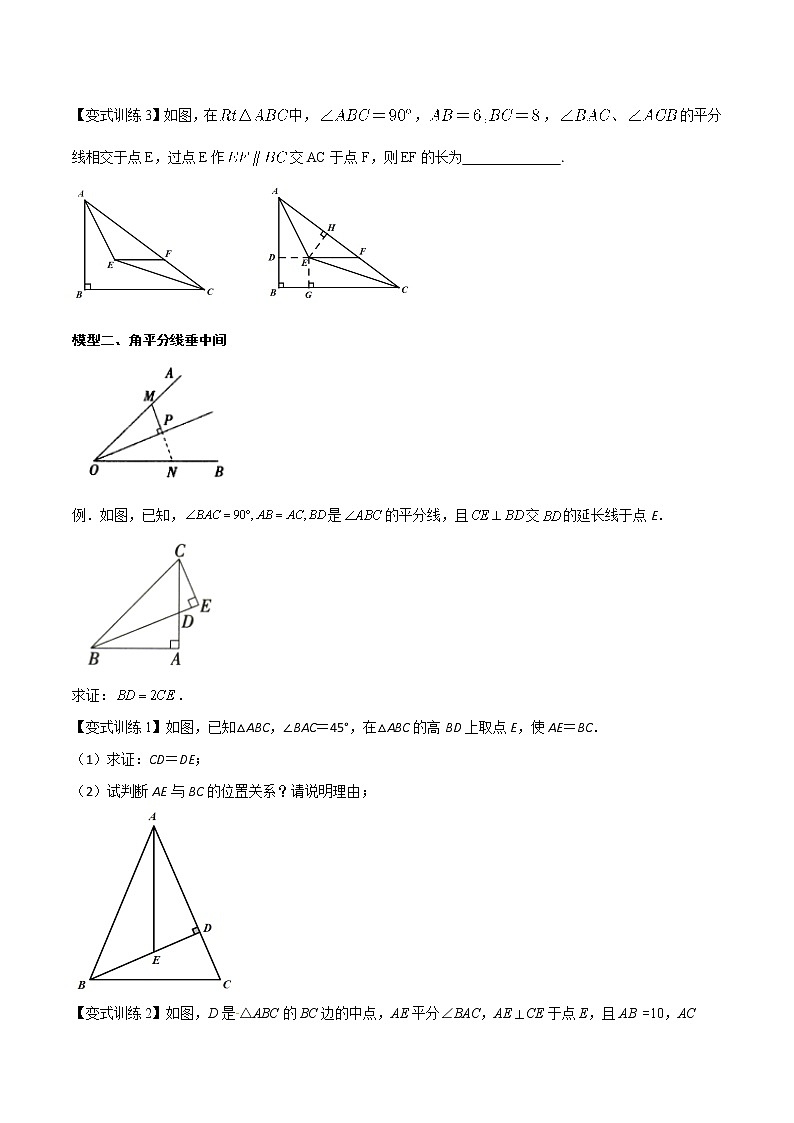
专题01 角平分线的五种模型模型一、角平分线垂两边 例1.如图，AD是△ABC的角平分线，且AB：AC＝3：2，则△ABD与△ACD的面积之比为（　　）A．3：2 B．6：4 C．2：3 D．不能确定【答案】A【详解】过点D作DE⊥AB于E，DF⊥AC于F．∵AD为∠BAC的平分线，∴DE=DF，又AB：AC=3：2，∴S△ABD：S△ACD=（AB•DE）：（AC•DF）=AB：AC=3：2．故选A．例2.如图，∠AOP＝∠BOP＝15°，PCOA，PD⊥OA，若PC＝4，则PD的长为 ___．【答案】2【详解】解：过P作PE⊥OB，交OB与点E，∵∠AOP＝∠BOP，PD⊥OA，PE⊥OB，∴PD＝PE，∵PCOA，∴∠CPO＝∠POD，又∠AOP＝∠BOP＝15°，∴∠CPO＝∠BOP＝15°，又∠ECP为△OCP的外角，∴∠ECP＝∠COP＋∠CPO＝30°，在直角三角形CEP中，∠ECP＝30°，PC＝4，∴PE＝PC＝2，则PD＝PE＝2．故答案为：2．【变式训练1】如图所示，在四边形ABCD中，DC//AB，∠DAB =90°，ACBC，AC =BC，∠ABC的平分线交AD，AC于点E、F，则的值是___________.【答案】【详解】解：如图，作FGAB于点G，∠DAB-90°，FG/AD， =ACBC，∠ACB =90°又BF平分∠ABC，FG =FC在Rt△BGF和Rt△BCF中△BGF≌△BCF（HL），BC =BGAC =BC，∠CBA =45°，AB =BC【变式训练2】如图，BD平分ABC的外角∠ABP，DA=DC，DE⊥BP于点E，若AB=5，BC=3，求BE的长．【答案】1【详解】解：过点D作BA的垂线交AB于点H，∵BD平分△ABC的外角∠ABP，DH⊥AB，∴DE＝DH，在Rt△DEB和Rt△DHB中，，∴Rt△DEB≌Rt△DHB（HL），∴BE＝BH，在Rt△DEC和Rt△DHA中，，∴Rt△DEC≌Rt△DHA（HL），∴AH＝CE，由图易知：AH＝AB−BH，CE＝BE＋BC，∴AB−BH＝BE＋BC，∴BE＋BH＝AB−BC＝5−3＝2，而BE＝BH，∴2BE＝2，故BE＝1．【变式训练3】如图，在中，，，、的平分线相交于点E，过点E作交AC于点F，则EF的长为              .【答案】【解析】延长FE交AB于点D，作于点G，作于点H，如图所示：四边形BDEG是矩形，平分，CE平分，四边形BDEG是正方形，在和中，，同理可得，设，则，，，解得，，，即，解得，. 模型二、角平分线垂中间 例．如图，已知，是的平分线，且交的延长线于点E．求证：．【答案】见解析【详解】证明：如图，延长与的延长线相交于点F，∵，∴，在和中，，∴，∴，∵是的平分线，∴．在和中，，∴，∴，∴，∴．【变式训练1】如图，已知△ABC，∠BAC＝45°，在△ABC的高BD上取点E，使AE＝BC．（1）求证：CD＝DE；（2）试判断AE与BC的位置关系？请说明理由；【答案】（1）见解析；（2），理由见解析；（3）【详解】（1）证明：∵，，∴，∴，在和中，∵ ∴，∴CD＝DE；（2），理由如下：如图，延长AE，交BC于点F，由（1）得，∵，∴，∴，即；【变式训练2】如图，D是△ABC的BC边的中点，AE平分∠BAC，AECE于点E，且AB =10，AC =16，则DE的长度为________          【答案】3【解答】解：如图，延长CE，AB交于点F.                       AE平分∠BAC，AEEC，∠FAE =∠CAE，∠AEF =∠AEC =90°在△AFE和△ACE中，，△AFE ≌ACE（ASA），AF =AC =16，EF =EC，BF =6又D是BC的中点，BD =CD，DE是△CBF的中位线，DE =BF=3，故答案为：3.【变式训练3】如图，在中，是的平分线，于点,//交于点，求证:.【答案】见解析【解答】证明：延长交于点.平分,  .又≌,.又∥,.模型三、角平分线+平行线构造等腰三角形例.如图所示，在△ABC中，BC =6，E、F分别是AB、AC的中点，动点P在射线EF上，BP交CE于D，∠CBP的平分线交CE于Q，当CQ =CE时，EP+BP =________.               【答案】12【解答】解：如图，延长BQ交射线EF于点M. E、F分别是AB、AC的中点，EF//BC，∠CBM =∠EMBBM平分∠ABC，∠ABM =∠CBM，∠EMB =∠EBM，EB =EM，EP +BP =EP +PM =EMCQ =CE，EQ =2CQ由EF//BC得，△EMQ∽△CBQ【变式训练1】如图，平分，于点C，，求OC的长？【答案】【解析】如图所示：过点D作交OA于点E，则，平分，，在中，，.【变式训练2】在中，∠C=90°，AD平分∠CAB，BE平分∠ABC，AD、BE相交于点F，且，则AC=　      　．【答案】【解析】过点E作于G，连接CF，如图所示：分别是和的平分线，，CF是的平分线，，在中，，由勾股定理可得.模型四、利用角平分线作对称例.已知：如图，在中，平分，求证：.【答案】见解析【解析】证明：在AB上截取，连接DE，如图所示：.【变式训练】AD是△ABC的角平分线，过点D作DE⊥AB于点E，且DE＝3，S△ABC＝20．（1）如图1，若AB＝AC，求AC的长；（2）如图2，若AB＝5，请直接写出AC的长．【答案】（1）；（2）【详解】解：（1）如图1，作DF⊥AC于F，∵AD是△ABC的角平分线，DE⊥AB，DF⊥AC，∴DF＝DE＝3，由题意得，×AB×3＋×AC×3＝20，解得，AC＝AB＝；（2）如图2，作DF⊥AC于F，∵AD是△ABC的角平分线，DE⊥AB，DF⊥AC，∴DF＝DE＝3，由题意得，×5×3＋×AC×3＝20，解得，AC＝．模型五、内外模型例.如图，在△ABC中，AB=AC，∠A=30°，E为BC延长线上一点，∠ABC与∠ACE的平分线相交于点D，则∠D的度数为（　　）A．15°             B．17.5°          C．20°           D．22.5°【答案】A【解析】∵∠ABC与∠ACE的平分线相交于点D，∴∠DCE=∠DCA，∠CBD=∠ABD，即，，.【变式训练】如图，的外角的平分线CP与内角的平分线BP交于点P，若，则           .【答案】【解析】是的外角，是的外角，平分平分，又，过点P分别作的延长线，垂足分别为点E、F、G，如图所示：由角平分线的性质可得，AP是的平分线，.课后训练1．如图，BD是ABC的外角∠ABP的角平分线，DA＝DC，DE⊥BP于点E，若AB＝5，BC＝3，则BE的长为（　　）A．2 B．1.5 C．1 D．0【答案】C【详解】解：如图，过点作于，是的角平分线，，DE⊥BP，，在和中，，，，在和中，，，，，，，，，，，解得：．故选：C．2．如图，是中的平分线，交于点E，交于点F，若，，，则的长为（ ）A． B．4 C．5 D．6【答案】A【详解】∵是中的平分线，于点E，交于点F，∴．又∵，，∴，∴．故选：A．3．如图，在Rt△ABC中，∠C＝90°，∠BAC的平分线交BC于点D，CD＝2，BD＝3，Q为AB上一动点，则DQ的最小值为（　　）A．1 B．2 C．2.5 D．【答案】B【详解】解：作DH⊥AB于H，如图，∵AD平分∠BAC，DH⊥AB，DC⊥AC，∴DH=DC=2，∵Q为AB上一动点，∴DQ的最小值为DH的长，即DQ的最小值为2．故选：B．4．如图，已知在四边形ABCD中，∠BCD＝90°，BD平分∠ABC，AB＝6，BC＝9，CD＝4，则四边形ABCD的面积是______．【答案】30【详解】过D作DE⊥AB，交BA的延长线于E，则∠E＝∠C＝90°，∵∠BCD＝90°，BD平分∠ABC，∴DE＝DC=4，∴四边形ABCD的面积S＝S△BCD＋S△BAD＝×BC×CD＋×AB×DE＝×9×4＋×6×4＝30，故答案为：30．5．如图，在△ABC中，AD为△ABC的角平分线，DE⊥AB，垂足为E，DF⊥AC，垂足为F，若AB=5，AC=3，DF=2，则△ABC的面积为______．【答案】8【详解】解：∵AD为△ABC的角平分线，DE⊥AB， DF⊥AC，∴DE=DF=2，∴△ABC的面积=×5×2+×3×2=8，故答案侍：8．6．在△ABC中，∠ABC＝62°，∠ACB＝50°，∠ACD是△ABC的外角 ∠ACD和∠ABC的平分线交于点E，则∠AEB＝_____︒【答案】25【详解】解：如图示：过点，分别作交于点，交于点，，交延长线于点，∵平分，平分，∴，，∴，∴平分，∵，，∴，∴，∵平分，∴在和中，∴，故答案是：25．7．如图，DE⊥AB于E，DF⊥AC于F，若BD=CD，BE=CF．（1）求证：AD平分∠BAC：（2）已知AC=18，BE=4，求AB的长．【答案】（1）见解析；（2）．【详解】（1）证明：，，，在和中，，∴，，，，平分；（2）解：，，，，，．8．如图1，在平面直角坐标系中，△ABC的顶点A（-4，0），B（0，4），AD⊥BC交BC于D点，交y轴正半轴于点E（0，t）（1）当t=1时，点C的坐标为       ；（2）如图2，求∠ADO的度数；（3）如图3，已知点P（0，3），若PQ⊥PC，PQ=PC，求Q的坐标（用含t的式子表示）．【答案】（1）点C坐标（1，0）；（2）∠ADO=45°；（3）Q（-3，3-t）．【详解】（1）如图1，当t=1时，点E（0，1），∵AD⊥BC，    ∴∠EAO+∠BCO=90°，∵∠CBO+∠BCO=90°，∴∠EAO=∠CBO，在△AOE和△BOC中，∵，∴△AOE≌△BOC（ASA），∴OE=OC=1，∴点C坐标（1，0）．故答案为：（1，0）；（2）如图2，过点O作OM⊥AD于点M，作ON⊥BC于点N，∵△AOE≌△BOC，∴S△AOE=S△BOC，且AE=BC，∵OM⊥AE，ON⊥BC，∴OM=ON，∴OD平分∠ADC；AD⊥BC，∴∠ADO=；（3）如图3，过P作GH∥x轴，过C作CG⊥GH于G，过Q作QH⊥GH于H，交x轴于F，∵P（0，3），C（t，0），∴CG=FH=3，PG=OC=t，∵∠QPC=90°，∴∠CPG+∠QPH=90°，∵∠QPH+∠HQP=90°，∴∠CPG=∠HQP，∵∠QHP=∠G=90°，PQ=PC，∴△PCG≌△QPH，∴CG=PH=3，PG=QH=t，∴Q（-3，3-t）