2020年云南省大理州中考数学一模测试卷4

这是一份2020年云南省大理州中考数学一模测试卷4，共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2020年云南省大理州中考数学一模测试卷4
一、选择题（本大题共8小题，共32.0分）
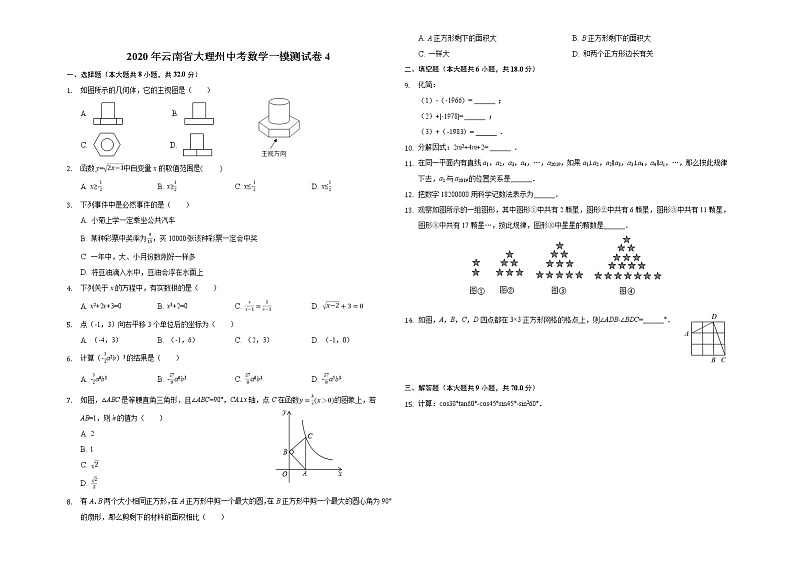
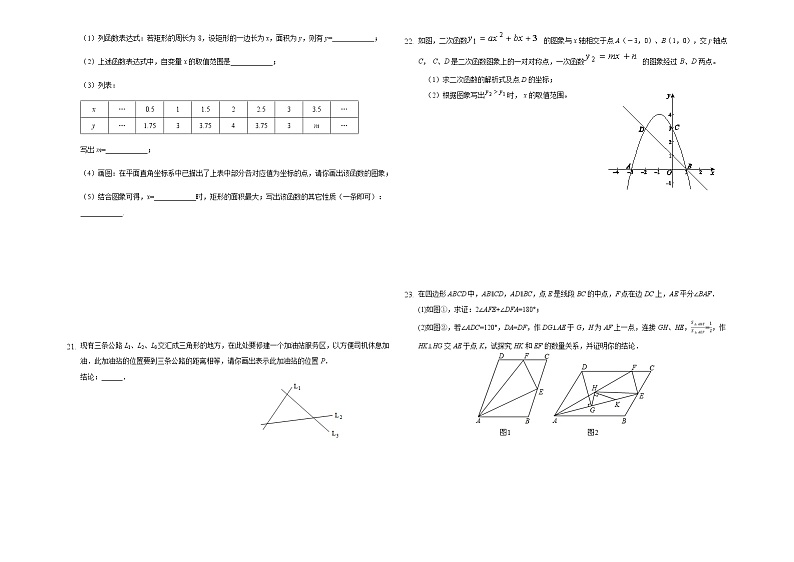
1. 如图所示的几何体，它的主视图是（　　）
A. B.
C. D.
2. 函数y=中自变量x的取值范围是( )
A. x≥- B. x≥ C. x≤- D. x≤
3. 下列事件中是必然事件的是（　　）
A. 小菊上学一定乘坐公共汽车
B. 某种彩票中奖率为，买10000张该种彩票一定会中奖
C. 一年中，大、小月份数刚好一样多
D. 将豆油滴入水中，豆油会浮在水面上
4. 下列关于x的方程中，有实数根的是（　　）
A. x2+2x+3=0 B. x3+2=0 C. D.
5. 点（-1，3）向右平移3个单位后的坐标为（　　）
A. （-4，3） B. （-1，6） C. （2，3） D. （-1，0）
6. 计算（-a2b）3的结果是（　　）
A. -a6b3 B. -a6b3 C. a6b3 D. -a5b3
7. 如图，△ABC是等腰直角三角形，且∠ABC=90°，CA⊥x轴，点C在函数的图象上，若AB=1，则k的值为（　　）
A. 2
B. 1
C.
D.
8. 有A、B两个大小相同正方形，在A正方形中剪一个最大的圆，在B正方形中剪一个最大的圆心角为90°的扇形，那么剪剩下的材料的面积相比（　　）
A. A正方形剩下的面积大 B. B正方形剩下的面积大
C. 一样大 D. 和两个正方形边长有关
二、填空题（本大题共6小题，共18.0分）
9. 化简：
（1）-（-1966）= ______ ； 
（2）+|-1978|= ______ ；  
（3）+（-1983）= ______ ．
10. 分解因式：2m2+4m+2= ______ ．
11. 在同一平面内有直线a1，a2，a3，a4，…，a2019，如果a1⊥a2，a2∥a3，a3⊥a4，a4∥as，…，那么按此规律下去，a1与a2019的位置关系是______．
12. 把数字18200000用科学记数法表示为______．
13. 观察如图所示的一组图形，其中图形①中共有2颗星，图形②中共有6颗星，图形③中共有11颗星，图形④中共有17颗星…，按此规律，图形⑩中星星的颗数是______．

14. 如图，A，B，C，D四点都在3×3正方形网格的格点上，则∠ADB-∠BDC=______°．




三、解答题（本大题共9小题，共70.0分）
15. 计算：cos30°tan60°-cos45°sin45°-sin260°．







16. 如图，PA、PB是⊙O的两条切线，点A、B为切点，直线OP交⊙O于点D、E，交AB于点C．
（1）写出圆中所有的垂直关系；
（2）写出图中所有的全等三角形.











17. 2014年5月12日，国家统计局公布了《2013年农民工监测调查报告》，报告显示：我国农民工收入持续快速增长．某地区农民工人均月收入增长率如图1，并将人均月收入绘制成如下图的不完整的条形统计图．

根据以上统计图解答下列问题：
（1）2013年农民工人均月收入的增长率是多少？
（2）2011年农民工人均月收入是多少？
（3）小明看了统计图后说：“农民工2012年的人均月收入比2011年的少了．”你认为小明的说法正确吗？请说明理由．



18. 列方程解应用题：
某市今年进行水网升级，1月1日起调整居民用水价格，每立方米水费上涨，小丽家去年12月的水费是15元，而今年5月的水费则是30元．已知小丽家今年5月的用水量比去年12月的用水量多5m3，求该市今年居民用水的价格．







19. 有4个完全相同的小球，把它们分别标号为1、2、3、4，放在一个口袋中，随机的摸出一个小球然后放回，再随机的摸出一个小球.
（1）采用树形图法（或列表法）列出两次摸球出现的所有可能结果，并回答两次摸球出现的所有可能结果共有几种.
（2）求两次摸出的球的标号相同的概率.
（3）求两次摸出的球的标号的和等于4的概率.





20. 某学习小组在学习了函数及函数图象的知识后，想利用此知识来探究周长一定的矩形其边长分别为多少时面积最大. 请将他们的探究过程补充完整.

（1）列函数表达式：若矩形的周长为8，设矩形的一边长为x，面积为y，则有y=____________；
（2）上述函数表达式中，自变量x的取值范围是____________；
（3）列表：
x
…
0.5
1
1.5
2
2.5
3
3.5
…
y
…
1.75
3
3.75
4
3.75
3
m
…
写出m=____________；
（4）画图：在平面直角坐标系中已描出了上表中部分各对应值为坐标的点，请你画出该函数的图象；
（5）结合图象可得，x=____________时，矩形的面积最大；写出该函数的其它性质（一条即可）：____________.







21. 现有三条公路L1、L2、L3交汇成三角形的地方，在此处要修建一个加油站服务区，以方便司机休息加油．此加油站的位置要到三条公路的距离相等，请你画出表示此加油站的位置P．
结论：______．








22. 如图，二次函数 的图象与x轴相交于点A（－3，0）、B（1，0），交y轴点C， C、D是二次函数图象上的一对对称点，一次函数的图象经过 B、D两点。
    （1）求二次函数的解析式及点D的坐标；
    （2）根据图象写出时， x的取值范围。
    









23. 在四边形ABCD中，AB∥CD，AD∥BC，点E是线段BC的中点，F点在边DC上，AE平分∠BAF．
(1)如图①，求证：2∠AFE+∠DFA=180°；
(2)如图②，若∠ADC=120°，DA=DF，作DG⊥AE于G，H为AF上一点，连接GH、HE，=，作HK⊥HG交AE于点K，试探究HK和EF的数量关系，并证明你的结论．






答案和解析

1.【答案】A

【解析】解：从正面看该组合体，底层是一个矩形，矩形的两侧分别由一条纵向的实线，上层是一个矩形．
故选：A．
根据主视图的意义，从正面看该组合体所得到的图形即可．
本题考查简单组合体的三视图，理解视图的意义，掌握主视图的画法是正确判断的关键．

2.【答案】B

【解析】试题分析：根据二次根式的性质，被开方数大于等于0，列不等式求解．
根据题意得：2x-1≥0
解得
故选B．

3.【答案】D

【解析】解：A．小菊上学一定乘坐公共汽车是随机事件；
B．某种彩票中奖率为，买10000张该种彩票会中奖是随机事件；
C．一年中大月份有7个，小月份有5个，不相等，是不可能事件；
D．将豆油滴入水中，豆油会浮在水面上是必然事件；
故选：D．
根据事件发生的可能性大小判断相应事件的类型即可．
考查了随机事件，解决本题需要正确理解必然事件、不可能事件、随机事件的概念．必然事件指在一定条件下一定发生的事件．不可能事件是指在一定条件下，一定不发生的事件．不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件．

4.【答案】B

【解析】解：A、x2+2x+3=0中，△=4-12=-8＜0，无实数根；
B、x3+2=0中，有实数根；
C、中,当分母x-1≠0，即x≠1，无实根；
D、+3=0中，被开方数a＜0，无实数根；
故选B
根据①分母=0，②中，被开方数a＜0时，③△＜0，满足①、②、③中的任何一个条件，方程都无实数根，
本题考查了不解方程来判别方程根的情况，依据是：一元二次方程ax2+bx+c=0（a≠0）的根与△=b2-4ac有如下关系：①当△＞0时，方程有两个不相等的两个实数根；②当△=0时，方程有两个相等的两个实数根；③当△＜0时，方程无实数根．

5.【答案】C

【解析】解：根据平移的规律可知：点A（-1，3）向右平移3个单位，得到的点的坐标为（2，3）．
故选：C．
移中点的变化规律是：横坐标右移加，左移减；纵坐标上移加，下移减．
本题考查平移的规律，在平面直角坐标系中，图形的平移与图形上某点的平移相同，注意平移规律的熟练运用．

6.【答案】B

【解析】解：（-a2b）3=（-）3a6b3=-a6b3．
故选：B．
直接利用记得乘方运算法则求出答案．
此题主要考查了积的乘方运算，正确掌握运算法则是解题关键．

7.【答案】B

【解析】解：∵等腰直角三角形ABC的顶点A、B分别在x轴、y轴的正半轴上，∠ABC=90°，CA⊥x轴，AB=1，
∴∠BAC=∠BAO=45°，
∴OA=OB=，AC=，
∴点C的坐标为（，），
∵点C在函数的图象上，
∴k=×=1，
故选：B．
根据题意可以求得OA和AC的长，从而可以求得点C的坐标，进而求得k的值．
本题考查反比例函数图象上点的坐标特征、等腰直角三角形，解答本题的关键是明确题意，利用数形结合的思想解答．

8.【答案】C

【解析】解：如图，设正方形的边长为2a．

则正方形中剪一个最大的圆的面积=πa2，正方形中剪一个最大的圆心角为90°的扇形的面积=•π•（2a）2=πa2，
∴圆的面积与扇形面积相等，
∴剪剩下的材料的面积一样大，
故选：C．
如图，设正方形的边长为2a．分别求出圆与扇形的面积，即可判断．
本题考查扇形的面积，正方形的性质等知识，解题的关键是理解题意，学会利用参数解决问题．

9.【答案】1966；1978；-1983

【解析】解：（1）-（-1966）=1966，
（2）+|-1978|=1978，
（3）+（-1983）=-1983，
故答案为：1966，1978，-1983．
（1）根据只有符号不同的两个数互为相反数，可得一个数的相反数；
（2）根据负数的绝对值是它的相反数，可得答案；
（3）根据在一个数的前面加上正号是原数，可得答案．
本题考查了相反数，在一个数的前面加上负号就是这个数的相反数，在一个数的前面加上正号是原数．

10.【答案】2（m+1）2

【解析】解：2m2+4m+2=2（m2+2n+1）=2（m+1）2．
故答案为：2（m+1）2．
首先提取公因式2，进而利用完全平方公式分解因式得出即可．
此题主要考查了提取公因式法以及公式法分解因式，熟练应用乘法公式是解题关键．

11.【答案】垂直

【解析】解：在同一平面内有直线两直线的位置
关系是相交或平行，如图所示：

∵a1⊥a2，a2∥a3，
∴a1 ⊥a3，
又∵a3⊥a4，
∴a1∥a4，
又∵a4∥as
∴a1∥a5，
又∵a5⊥a6，
∴a1⊥a6，
又∵a6∥a7，
∴a1⊥a7，
…
从以上的规律可知：a1与an的位置关系是4为周期进行循环，
若下角标的余数为0或1时与a1平行；若下角标的余数为2或3时与a1垂直．
∵2019=4×504+3，
∴a1⊥a2019，
故答案为：垂直．
从已知两直线的位置关系，运用平行线的性质，观察分析得几条特殊直线与a1的位置关系为a1∥a4，a1∥a5；a1⊥a2，a1 ⊥a3；且a1与an的位置关系是4为周期进行循环，下角标的余数为0或1时与a1平行，下角标的余数为2或3时与a1垂直，计算2019=4×504+3，余数为3判定两直线的位置关系为a1⊥a2019．
本题综合考查了平行线的性质，同一平面内图形的变化规律，倍数和余数的运用等相关知识点，重点是掌握平行线的性质，难点是掌握由特殊到一般图形变化规律在几何中的运用．

12.【答案】1.82×107

【解析】
【分析】
​​​​​​​此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．
科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正数；当原数的绝对值＜1时，n是负数．
【解答】
解：将18200000用科学记数法表示为1.82×107．
故答案为：1.82×107．  
13.【答案】74

【解析】解：设图形n中星星的颗数是an（n为正整数），
∵a1=2=1+1，
a2=6=（1+2）+3，
a3=11=（1+2+3）+5，
a4=17=（1+2+3+4）+7，
∴an=1+2+…+n+（2n-1）=+（2n-1）=n2+n-1．
∴a10=×102+×10-1=50+25-1=74．
故答案为：74．
设图形n中星星的颗数是an（n为正整数），列出部分图形中星星的个数，根据数据的变化找出变化规律n2+n-1，依此规律即可得出结论．
本题考查了规律型中的图形的变化类，根据图形中数的变化找出变化规律是解题的关键．

14.【答案】45

【解析】解：如图，找到C点关于DB的对应点，连结DE，AE，
则∠EDB=∠CDB，
则∠ADB-∠BDC=∠ADB-∠BDE=∠ADE，
∵AD=AE==，
DE==，
（）2+（）2=（）2，
∴△EAD是等腰直角三角形，
∴∠ADE=45°，即∠ADB-∠BDC=45°．
故答案为：45．
根据轴对称图形的性质得到∠EDB=∠CDB，可得∠ADB-∠BDC=∠ADE，根据勾股定理和勾股定理的逆定理得到△EAD是等腰直角三角形，再根据等腰直角三角形的性质即可求解．
此题主要考查了轴对称、勾股定理和勾股定理的逆定理、等腰直角三角形的性质，得出∠ADB-∠BDC=∠ADE是解题关键．

15.【答案】解：原式=×-×-（）2
=--
=．

【解析】把特殊角的三角函数值代入算式，计算即可．
本题考查的是特殊角的三角函数值的计算，解决此类题目的关键是熟记特殊角的三角函数值．

16.【答案】解：（1）OA⊥PA，OB⊥PB，AB⊥OP；
（2）△APO≌△BPO；△AOC≌△BOC；△APC≌△BPC.

【解析】（1）利用切线的性质得到OA⊥PA，OB⊥PB；再由切线定理得PA=PB，OP平分∠APB，然后根据等腰三角形的性质可判断AB⊥OP；
（2）根据“HL”判断△APO≌△BPO，△AOC≌△BOC；△APC≌△BPC；
本题考查了切线的性质：圆的切线垂直于经过切点的半径．注意构造直角三角形．

17.【答案】解：（1）由折线统计图可得出：
2013年农民工人均月收入的增长率是：10%；

（2）由条形统计图可得出：
2011年农民工人均月收入是：2205元；

（3）不正确，
理由：∵2012年农民工人均月收入是：2205×（1+20%）=2646（元）＞2205元，
∴农民工2012年的人均月收入比2011年的少了，是错误的．

【解析】（1）直接利用折线统计图得出答案即可；
（2）直接利用条形统计图得出答案即可；
（3）利用2012年农民工人均月收入增长率进而求出2012年的月平均收入，进而得出答案．
此题主要考查了条形统计图以及折线统计图的应用，利用图形获取正确信息是解题关键．

18.【答案】解：设该市去年居民用水的价格为x元/m3．
由题意：-=5，
解得x=，
经检验：x=是分式方程的解．
×（1+）=2（元/m3），
答：该市今年居民用水的价格为2元/m3

【解析】设该市去年居民用水的价格为x元/m3．构建分式方程即可解决问题；
本题考查分式方程的应用，解题的关键是正确寻找等量关系，构建分式方程解决问题，注意解分式方程，必须检验．

19.【答案】解：（1）画树状图如下：

两次摸球出现的所有可能结果共有16种；

（2）两次摸出的球的标号相同有4种，
所以，P（两次摸出的球的标号相同）==；

（3）两次摸出的球的标号的和等于4有3次，
所以，P（两次摸出的球的标号的和等于4）=．

【解析】（1）画出树状图，然后即可得解；
（2）根据树状图，利用概率公式列式计算即可得解；
（3）根据概率公式列式进行计算即可得解．
本题用到的知识点为：概率=所求情况数与总情况数之比．

20.【答案】解：（1）-x2 + 4 x；
（2）0＜x＜4；
（3）1.75；
（4）如图所示: 

（5）2；当0＜x≤2时，y随x的增大而增大.


【解析】
【分析】
本题考查了二次函数的图像，二次函数的性质，二次函数的最值，矩形的性质.
（1）根据矩形的面积可得答案;
（2）根据矩形的性质，结合解析式可得：0＜x＜4；
（3）计算可得：m=1.75；
（4）根据（3）中数据，画出函数的图象；
（5）结合图象可得：轴对称图形；x=2时，矩形的面积最大；该函数的性质：当0＜x≤2时，y随x的增大而增大.
【解答】
解：（1）若矩形的周长为8，设矩形的一边长为x，面积为y，则有y=-x2 + 4 x;
（2）根据矩形的性质，结合解析式可得：0＜x＜4；
（3）计算可得：m=1.75；
（4）图示见答案；
（5）结合图象可得：轴对称图形；
x=2时，矩形的面积最大；
该函数的性质：当0＜x≤2时，y随x的增大而增大；
故答案为（1）-x2 + 4 x；（2）0＜x＜4；（3）1.75；（5）2；当0＜x≤2时，y随x的增大而增大.
  
21.【答案】作∠ABC与∠ACB的平分线，两条角平分线交于点P，则点P即为所求点

【解析】解：如图所示：

①以点B为圆心，以任意长为半径画圆，分别交AB、BC于点D、E；
②分别以点D、E为圆心，以大于DE为半径画圆，两圆相交于点F．连接BF，则BF即为∠ABC的平分线；
同理作出∠ACB的平分线，两条角平分线交于点P，则点P即为所求点．
故答案为作∠ABC与∠ACB的平分线，两条角平分线交于点P，则点P即为所求点．
分别作∠ABC与∠ACB的平分线，两条角平分线交于点P，则点P即为所求点．
本题考查的是作图-应用与设计作图，熟知角平分线上的点到角两边距离相等的性质是解答此题的关键，属于基础题目，中考常考题型．

22.【答案】  （1）二次函数过点A（－3，0）、B（1，0）
    ∴   解得   
    ∴二次函数解析式为y=-x2-2 x+3       
     则c点坐标为（0,3）  又由抛物线解析式可得其对称轴为直线x= -1
    ∴ C点的对称点D的坐标为（-2，3）       
    （2）由抛物线图象知，当y2>y1时，x1

【解析】试题分析：本题考查待定系数法求二次函数解析式。在利用待定系数法求二次函数关系式时，要根据题目给定的条件，选择恰当的方法设出关系式，从而代入数值求解。一般地，当已知抛物线上三点时，常选择一般式，用待定系数法列三元一次方程组来求解；当已知抛物线的顶点或对称轴时，常设其解析式为顶点式来求解；当已知抛物线与x轴有两个交点时，可选择设其解析式为交点式来求解。
考点：待定系数法求二次函数解析式

23.【答案】(1)证明：延长AE、BC相交于点M．
∵四边形ABCD是平行四边形，
∴ DC∥AB，
∴∠2=∠ M．
∵ AE平分∠BAF，
∴∠1=∠2．
∴∠1=∠ M．
∵ E是线段BC的中点，
∴ BE=CE．
在△ ABE和△MCE中
，
∴△ ABE≌△MCE(AAS)，
∴ AE=ME．
∵ AF=MF，
∴∠ AFE=∠CFE．∠AEF=90°．
∵∠ AFM+∠DFA=180°，
∴∠ AFE+∠MFE+∠DFA=180°，
即2∠ AFE+∠DFA=180°；



(2)解：HK=EF．
∵ AD=DF，∠ADC=120°，
∴∠1=∠2=30°．
∵ DC∥AB，∠DAB=60°，
∴∠ BAF=30°．
∵ AE平分∠BAF，
∴∠3=∠4=15°，
∴∠1+∠3=45°．
∵ DG⊥AE，
∴∠ DGA=90°，
∴∠ ADG=45°，
∴∠ ADG=∠DAG，
∴ AG=DG．
作 EM⊥AF于点M．

∵=，
∴，
∴ AH=FH．
∴ H为AF的中点．
作 HI⊥BE于I，
∴∠ HIA=∠HIK=90°，
∴∠ AIH=∠AEF，
∴ HI∥EF，
∴．
PG⊥HG交AF于点P，
∴∠ PGH=90°，
∴∠ AGD=∠PGH，
∴∠ AGD-∠PGD=∠PGH-∠PGD，
∴∠6=∠7．
在△ AGP和△DGH中，
，
∴△ AGP≌△DGH(ASA)，
∴ PG=HG，
∴∠ HPG=∠3+∠6=45°，
∴∠6=30°．
∵ HK⊥HG，
∴∠ GHK=90°，
∴∠ GHK=∠PGH，
∴ PG∥HE，
∴∠ HKG=∠6=30°，
∴，
∴，
∴ HK=EF．

【解析】(1)延长AE、BC相交于点M，根据平行四边形的性质就可以得出∠1=∠M．∠B=∠MCE，通过证明△ABE≌△MCE就可以得出AE=EM，就可以得出∠AFE=∠CFE，进而得出结论；
(2)连接DH，作HI⊥BE于I，PG⊥HG交AF于点P，根据平行四边形的性质就可以得出GA=GD，就可以得出△GPA≌△GHD，就可以求出∠6=∠GKH=30°，得出，由就可以得出结论．