中考数学一轮全程复习课时练第43课时《开放与探究型问题》(学生版)

这是一份中考数学一轮全程复习课时练第43课时《开放与探究型问题》(学生版)，共5页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。


一、选择题
1．如图，点A，B，C在一条直线上，△ABD，△BCE均为等边三角形，连结AE和CD，AE分别交CD，BD于点M，P，CD交BE于点Q，连结PQ，BM，下面结论：①△ABE≌△DBC；②∠DMA＝60°；③△BPQ为等边三角形；④MB平分∠AMC，
其中结论正确的有( )
A．1个 B．2个 C．3个 D．4个
2．如图，AC是矩形ABCD的对角线，⊙O是△ABC的内切圆，现将矩形ABCD按如图所示的方式折叠，使点D与点O重合，折痕为FG，点F，G分别在边AD，BC上，连结OG，DG，若OG⊥DG，且⊙O的半径长为1，则下列结论不成立的是 ( )
A．CD＋DF＝4
B．CD－DF＝2eq \r(3)－3
C．BC＋AB＝2eq \r(3)＋4
D．BC－AB＝2
二、填空题
3．如图，正方形ABCD边长为1，以AB为直径作半圆，点P是CD中点，BP与半圆交于点Q，连结DQ.给出如下结论：①DQ＝1；②eq \f(PQ,BQ)＝eq \f(3,2)；③S△PDQ＝eq \f(1,8)；④cs∠ADQ＝eq \f(3,5).其中正确结论是____.(填写序号)

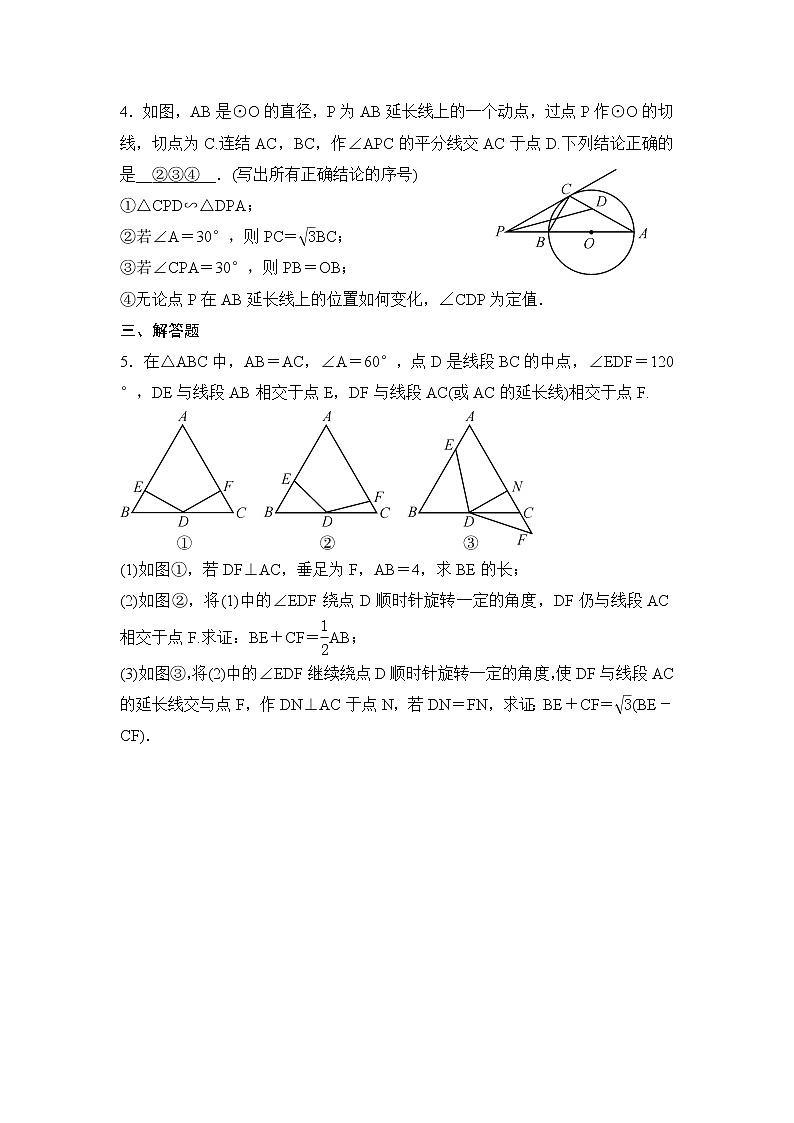
4．如图，AB是⊙O的直径，P为AB延长线上的一个动点，过点P作⊙O的切线，切点为C.连结AC，BC，作∠APC的平分线交AC于点D.下列结论正确的是__②③④__．(写出所有正确结论的序号)
①△CPD∽△DPA；
②若∠A＝30°，则PC＝eq \r(3)BC；
③若∠CPA＝30°，则PB＝OB；
④无论点P在AB延长线上的位置如何变化，∠CDP为定值．
三、解答题
5．在△ABC中，AB＝AC，∠A＝60°，点D是线段BC的中点，∠EDF＝120°，DE与线段AB相交于点E，DF与线段AC(或AC的延长线)相交于点F.
(1)如图①，若DF⊥AC，垂足为F，AB＝4，求BE的长；
(2)如图②，将(1)中的∠EDF绕点D顺时针旋转一定的角度，DF仍与线段AC相交于点F.求证：BE＋CF＝eq \f(1,2)AB；
(3)如图③，将(2)中的∠EDF继续绕点D顺时针旋转一定的角度，使DF与线段AC的延长线交与点F，作DN⊥AC于点N，若DN＝FN，求证：BE＋CF＝eq \r(3)(BE－CF)．
6．(1)如图①，已知△ABC，以AB，AC为边向△ABC外作等边△ABD和等边△ACE，连结BE，CD.请你完成图形，并证明：BE＝CD；(尺规作图，不写作法，保留作图痕迹)
(2)如图②，已知△ABC，以AB，AC为边向外作正方形ABFD和正方形ACGE，连结BE，CD.BE与CD有什么数量关系？简单说明理由；
(3)运用(1)(2)解答中积累的经验和知识，完成下题：如图③，要测量池塘两岸相对的两点B，E的距离，已经测得∠ABC＝45°，∠CAE＝90°，AB＝BC＝100 m，AC＝AE，求BE的长．
7．如图，矩形ABCD中，AD＝2AB，E是AD边上一点，DE＝eq \f(1,n)AD(n为大于2的整数)，连结BE，作BE的垂直平分线分别交AD，BC于点F，G，FG与BE的交点为O，连结BF和EG.
(1)试判断四边形BFEG的形状，并说明理由；
(2)当AB＝a(a为常数)，n＝3时，求FG的长；
(3)记四边形BFEG的面积为S1，矩形ABCD的面积为S2，当eq \f(S1,S2)＝eq \f(17,30)时，求n的值．
8．如图，已知AB是圆O的切线，切点为B，直线AO交圆O于C，D两点，CD＝2，∠DAB＝30°，动点P在直线AB上运动，PC交圆O于另一点Q.
(1)当点P运动到Q，C两点重合时(如图①)，求AP的长；
(2)点运动过程中，有几个位置(几种情况)使△CQD的面积为eq \f(1,2)？(直接写出答案)
(3)当使△CQD的面积为eq \f(1,2)，且Q位于以CD为直径的上半圆上，CQ＞QD时(如图②)，求AP的长．
10．类比等腰三角形的定义，我们定义：有一组邻边相等的凸四边形叫做“等邻边四边形”．
(1)概念理解
如图43－10①，在四边形ABCD中，添加一个条件使得四边形ABCD是“等邻边四边形”．请写出你添加的一个条件；
(2)问题探究
①小红猜想：对角线互相平分的“等邻边四边形”是菱形．她的猜想正确吗？请说明理由；
②如图②，小红画了一个Rt△ABC，其中∠ABC＝90°，AB＝2，BC＝1，并将Rt△ABC沿∠ABC的平分线BB′方向平移得到△A′B′C′，连结AA′，BC′.小红要使平移后的四边形ABC′A′是“等邻边四边形”，应平移多少距离(即线段BB′的长)?
(3)应用拓展
如图③，“等邻边四边形”ABCD中，AB＝AD，∠BAD＋∠BCD＝90°，AC，BD为对角线，AC＝eq \r(2)AB.试探究BC，CD，BD的数量关系．