考点17解直角三角形（解析版）-2022年数学中考一轮复习考点透析（华师大版）

这是一份考点17解直角三角形（解析版）-2022年数学中考一轮复习考点透析（华师大版），共22页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
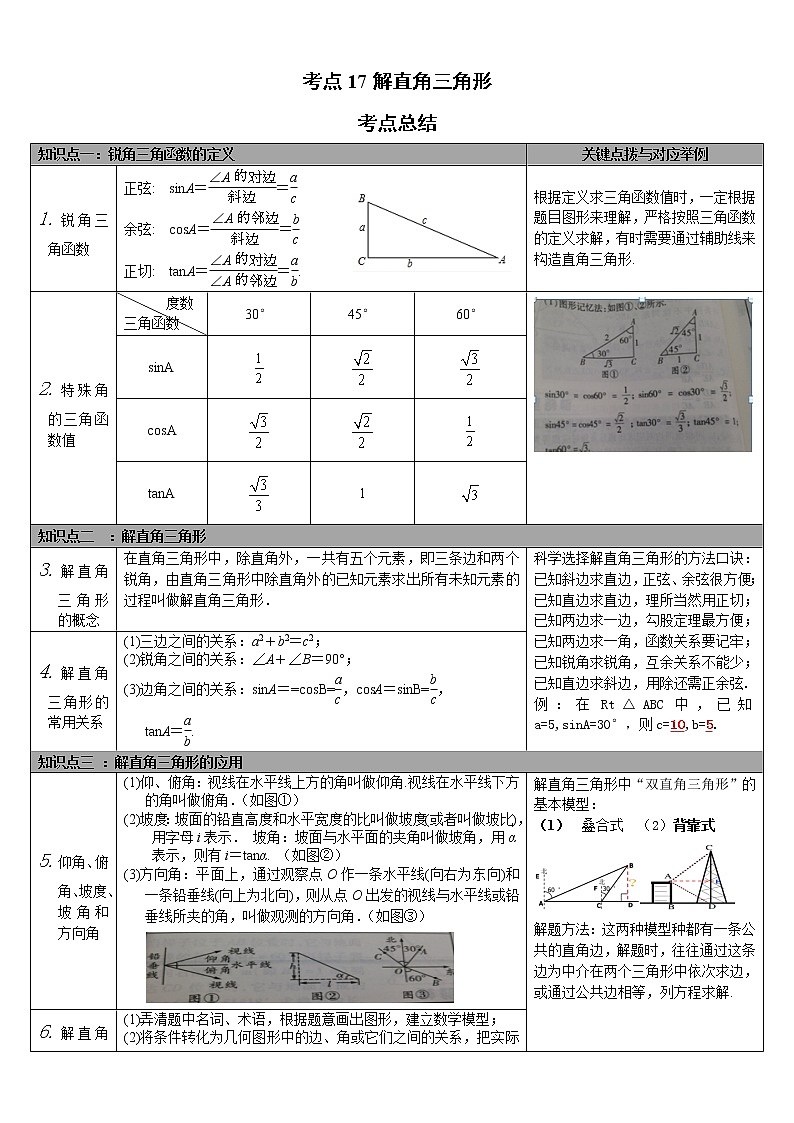
考点17解直角三角形考点总结知识点一：锐角三角函数的定义             关键点拨与对应举例1.锐角三角函数正弦:  sinA＝＝余弦:  cosA＝＝正切:  tanA＝＝. 根据定义求三角函数值时，一定根据题目图形来理解，严格按照三角函数的定义求解，有时需要通过辅助线来构造直角三角形.2.特殊角的三角函数值      度数三角函数30°45°60°sinAcosAtanA1知识点二  ：解直角三角形3.解直角三角形的概念在直角三角形中，除直角外，一共有五个元素，即三条边和两个锐角，由直角三角形中除直角外的已知元素求出所有未知元素的过程叫做解直角三角形．科学选择解直角三角形的方法口诀：已知斜边求直边，正弦、余弦很方便；已知直边求直边，理所当然用正切；已知两边求一边，勾股定理最方便；已知两边求一角，函数关系要记牢；已知锐角求锐角，互余关系不能少；已知直边求斜边，用除还需正余弦.例：在Rt△ABC中，已知a=5,sinA=30°，则c=10,b=5.4.解直角三角形的常用关系(1)三边之间的关系：a2＋b2＝c2； (2)锐角之间的关系：∠A＋∠B＝90°；(3)边角之间的关系：sinA＝=cosB=，cosA＝sinB=，tanA＝.知识点三 ：解直角三角形的应用5.仰角、俯角、坡度、坡角和方向角(1)仰、俯角：视线在水平线上方的角叫做仰角.视线在水平线下方的角叫做俯角．（如图①）(2)坡度：坡面的铅直高度和水平宽度的比叫做坡度(或者叫做坡比)，用字母i表示． 坡角：坡面与水平面的夹角叫做坡角，用α表示，则有i＝tanα. （如图②）(3)方向角：平面上，通过观察点Ο作一条水平线(向右为东向)和一条铅垂线(向上为北向)，则从点O出发的视线与水平线或铅垂线所夹的角，叫做观测的方向角．（如图③）解直角三角形中“双直角三角形”的基本模型：（1）          叠合式  （2）背靠式解题方法：这两种模型种都有一条公共的直角边，解题时，往往通过这条边为中介在两个三角形中依次求边，或通过公共边相等，列方程求解.6.解直角三角形实际应用的一般步骤(1)弄清题中名词、术语，根据题意画出图形，建立数学模型；(2)将条件转化为几何图形中的边、角或它们之间的关系，把实际问题转化为解直角三角形问题；(3)选择合适的边角关系式，使运算简便、准确；(4)得出数学问题的答案并检验答案是否符合实际意义，从而得到问题的解． 真题演练 一、单选题1．（2021·山东青岛·中考真题）如图，在四边形纸片中，，，．将纸片折叠，使点落在边上的点处，折痕为．若，则的长为（    ）A．5 B． C． D．【答案】C【分析】过点A作 于H，由折叠知识得： ，再由锐角三角函数可得，然后根据，可证得四边形AHFG是矩形，即可求解．【详解】解：过点A作 于H，由折叠知：BF=GF，∠BFE=∠GFE，， ，在 中，，， ，， ， ， 四边形AHFG是矩形， ， ．故选：C．2．（2021·山东济南·中考真题）无人机低空遥感技术已广泛应用于农作物监测．如图，某农业特色品牌示范基地用无人机对一块试验田进行监测作业时，在距地面高度为的处测得试验田右侧出界处俯角为，无人机垂直下降至处，又测得试验田左侧边界处俯角为，则，之间的距离为（参考数据：，，，，结果保留整数）（    ）A． B．C． D．【答案】C【分析】根据题意易得OA⊥MN，∠N=43°，∠M=35°，OA=135m，AB=40m，然后根据三角函数可进行求解．【详解】解：由题意得：OA⊥MN，∠N=43°，∠M=35°，OA=135m，AB=40m，∴，∴，，∴；故选C．3．（2021·山东日照·中考真题）如图，在一次数学实践活动中，小明同学要测量一座与地面垂直的古塔的高度，他从古塔底部点处前行到达斜坡的底部点处，然后沿斜坡前行到达最佳测量点处，在点处测得塔顶的仰角为，已知斜坡的斜面坡度，且点，，，，在同一平面内，小明同学测得古塔的高度是（　　）A． B． C． D．【答案】A【分析】过作于，于，得到，，设，，根据勾股定理得到，求得，，，于是得到结论．【详解】解：过作于，于，，，斜坡的斜面坡度，，设，，，，，，，，，，故选：A．4．（2021·山东滨州·中考真题）如图，是的外接圆，CD是的直径．若，弦，则的值为（    ）A． B． C． D．【答案】A【分析】连接AD，根据直径所对的圆周角等于90°和勾股定理，可以求得AD的长，然后即可求得∠ADC的余弦值，再根据同弧所对的圆周角相等，可以得到∠ABC=∠ADC，从而可以得到cos∠ABC的值．【详解】解：连接AD，如右图所示，∵CD是⊙O的直径，CD=10，弦AC=6，∴∠DAC=90°，∴AD==8，∴cos∠ADC==，∵∠ABC=∠ADC，∴cos∠ABC的值为，故选：A．5．（2021·山东淄博·中考真题）如图，在中，是斜边上的中线，过点作交于点．若的面积为5，则的值为（    ）A． B． C． D．【答案】A【分析】由题意易得，设，则有，则有，，然后可得，过点C作CH⊥AB于点H，进而根据三角函数及勾股定理可求解问题．【详解】解：∵，，∴，∴，∵是斜边上的中线，∴，设，则有，∵，∴由勾股定理可得，∵的面积为5，∴，∵，∴，即，化简得：，解得：或，当时，则AC=2，与题意矛盾，舍去；∴当时，即，过点C作CH⊥AB于点H，如图所示：∴，，，∴，，∴，∴，∴；故选A．6．（2021·山东威海·中考真题）若用我们数学课本上采用的科学计算器计算sin3618＇，按键顺序正确的是（    ）A．B．C．D．【答案】D【分析】根据计算器按键顺序计算即可．【详解】解：根据计算器的按键顺序可知，正确的按键顺序为D选项，故选：D．7．（2021·山东威海·中考真题）如图，在菱形ABCD中，，，点P，Q同时从点A出发，点P以1cm/s的速度沿A﹣C﹣D的方向运动，点Q以2cm/s的速度沿A﹣B﹣C﹣D的方向运动，当其中一点到达D点时，两点停止运动．设运动时间为x（s），的面积为y（cm2），则下列图象中能大致反映y与x之间函数关系的是（    ）A． B．C． D．【答案】A【分析】先证明∠CAB=∠ACB=∠ACD=60°，再分0≤x≤1、1＜x≤2、2＜x≤3三种情况画出图形，求出函数解析式，根据二次函数、一次函数图象与性质逐项排除即可求解．【详解】解：∵四边形ABCD是菱形，∴AB=BC=CD=AD，∠B=∠D=60°，∴△ABC，ACD都是等边三角形，∴∠CAB=∠ACB=∠ACD=60°．如图1，当0≤x≤1时，AQ=2x，AP=x，作PE⊥AB于E，∴，∴，故D选项不正确；如图2，当1＜x≤2时，CP=2-x，CQ=4-2x，BQ=2x-2，作PF⊥BC与F，作QH⊥AB于H，∴，，∴，故B选项不正确；当2＜x≤3时，CP=x-2，CQ=2x-4，∴PQ=x-2，作AG⊥CD于G，∴，∴，故C不正确．故选：A8．（2021·山东东营·中考真题）如图，在中，，，，若用科学计算器求AC的长，则下列按键顺序正确的是（    ）A． B．C． D．【答案】D【分析】根据正切函数的定义，可得，根据计算器的应用，可得答案．【详解】解：由，得：，故选：D．9．（2021·山东泰安·中考真题）如图，四边形是的内接四边形，，，，，则的长为（   ）A． B． C． D．2【答案】C【分析】如图，延长AD，BC，二线交于点E，可求得∠E=30°，在Rt△CDE中，利用tan30°计算DE，在Rt△ABE中，利用sin30°计算AE，根据AD=AE-DE求解即可；【详解】如图，延长AD，BC，二线交于点E，∵∠B=90°，∠BCD=120°，∴∠A=60°，∠E=30°，∠ADC=90°，∴∠ADC=∠EDC= 90°，在Rt△CDE中，tan30°=，∴DE==，在Rt△ABE中，sin30°=，∴AB==4，∴AD=AE-DE=,故选C10．（2021·山东泰安·中考真题）如图，在中，，以点A为圆心，3为半径的圆与边相切于点D，与，分别交于点E和点G，点F是优弧上一点，，则的度数是（   ）A．50° B．48° C．45° D．36°【答案】B【分析】连接AD，由切线性质可得∠ADB=∠ADC=90°，根据AB=2AD及锐角的三角函数可求得∠BAD=60°，易求得∠ADE=72°，由AD=AE可求得∠DAE=36°，则∠GAC=96°，根据圆周角定理即可求得∠GFE的度数．【详解】解：连接AD，则AD=AG=3，∵BC与圆A相切于点D，∴∠ADB=∠ADC=90°，在Rt△ADB中，AB=6，则cos∠BAD==，∴∠BAD=60°，∵∠CDE=18°，∴∠ADE=90°﹣18°=72°，∵AD=AE，∴∠ADE=∠AED=72°，∴∠DAE=180°﹣2×72°=36°，∴∠GAC=36°+60°=96°，∴∠GFE=∠GAC=48°，故选：B． 二、填空题11．（2021·山东滨州·中考真题）如图，在中，，，．若点P是内一点，则的最小值为____________．【答案】【分析】根据题意，首先以点A为旋转中心，顺时针旋转△APB到△AP′B′，旋转角是60°，作出图形，然后根据旋转的性质和全等三角形的性质、等边三角形的性质，可以得到PA+PB+PC=PP′+P′B′+PC，再根据两点之间线段最短，可以得到PA+PB+PC的最小值就是CB′的值，然后根据勾股定理可以求得CB′的值，从而可以解答本题．【详解】解：以点A为旋转中心，顺时针旋转△APB到△AP′B′，旋转角是60°，连接BB′、PP′，，如图所示，则∠PAP′=60°，AP=AP′，PB=P′B′，∴△APP′是等边三角形，∴AP=PP′，∴PA+PB+PC=PP′+P′B′+PC，∵PP′+P′B′+PC≥CB′，∴PP′+P′B′+PC的最小值就是CB′的值，即PA+PB+PC的最小值就是CB′的值，∵∠BAC=30°，∠BAB′=60°，AB==2，∴∠CAB′=90°，AB′=2，AC=AB•cos∠BAC=2×cos30°=，∴CB′=，故答案为：．12．（2021·山东淄博·中考真题）两张宽为的纸条交叉重叠成四边形，如图所示．若，则对角线上的动点到三点距离之和的最小值是__________．【答案】【分析】由题意易得四边形是菱形，过点D作DE⊥BC于点E，连接AC，交BD于点O，易得，，然后根据勾股定理可得，则，，进而可得，要使为最小，即的值为最小，则可过点A作AM⊥AP，且使，连接BM，最后根据“胡不归”问题可求解．【详解】解：∵纸条的对边平行，即，∴四边形是平行四边形，∵两张纸条的宽度都为，∴，∴，∴四边形是菱形，过点D作DE⊥BC于点E，连接AC，交BD于点O，如图所示：∴，∴，∴，∵，，∴，，∴，∴，∴，，∴，过点A作AM⊥AP，且使，连接BM，如图所示：∴，要使的值为最小，则需满足为最小，根据三角不等关系可得：，所以当B、P、M三点共线时，取最小，即为BM的长，如图所示：∴，∴，∴的最小值为，即的最小值为；故答案为．13．（2021·山东济宁·中考真题）如图，中，，，，点O为的中点，以O为圆心，以为半径作半圆，交于点D，则图中阴影部分的面积是____．
 【答案】【分析】根据题意，作出合适的辅助线，即可求得DE的长、的度数，然后根据图形可知阴影部分的面积是的面积减去的面积和扇形的面积，从而可以解答本题．【详解】解：连接OD，过点D作于E，
在中，∴，，∴，∴，∵，∴，∴阴影部分的面积是：，故答案为：．14．（2021·山东威海·中考真题）如图，先将矩形纸片ABCD沿EF折叠（AB边与DE在CF的异侧），AE交CF于点G；再将纸片折叠，使CG与AE在同一条直线上，折痕为GH．若，纸片宽，则HE＝__________cm．【答案】【分析】根据题意，证明四边形是平行四边形，运用的正弦和余弦的关系，求出HE．【详解】如图，分别过作， 垂足分别为则根据题意，，因为折叠，则四边形ABCD是矩形同理四边形是平行四边形，中，故答案为：．15．（2021·山东东营·中考真题）如图，正方形中，，AB与直线l所夹锐角为，延长交直线l于点，作正方形，延长交直线l于点，作正方形，延长交直线l于点，作正方形，…，依此规律，则线段________．【答案】【分析】利用tan30°计算出30°角所对直角边，乘以2得到斜边，计算3次，找出其中的规律即可.【详解】∵AB与直线l所夹锐角为，正方形中，，∴∠=30°，∴=tan30°==1，∴；∵=1，∠=30°，∴=tan30°=，∴；∴线段,故答案为：. 三、解答题16．（2021·山东青岛·中考真题）某校数学社团开展“探索生活中的数学”研学活动，准备测量一栋大楼的高度．如图所示，其中观景平台斜坡的长是20米，坡角为，斜坡底部与大楼底端的距离为74米，与地面垂直的路灯的高度是3米，从楼顶测得路灯项端处的俯角是．试求大楼的高度．（参考数据：，，，，，）【答案】96米【分析】延长AE交CD延长线于M，过A作AN⊥BC于N，则四边形AMCN是矩形，得NC=AM，AN=MC，由锐角三角函数定义求出EM、DM的长，得出AN的长，然后由锐角三角函数求出BN的长，即可求解．【详解】延长交于点，过点作，交于点，由题意得，，∴四边形为矩形，∴，.在中，，∴，，∴，，∴，∴.在中，，∴，∴，∴，∴.答：大楼的高度约为96米.17．（2021·山东济南·中考真题）已知：如图，是的直径，，是上两点，过点的切线交的延长线于点，，连接，．（1）求证：；（2）若，，求的半径．【答案】（1）见解析；（2）【分析】（1）连接，根据切线的性质，已知条件可得，进而根据平行线的性质可得，根据圆周角定理可得，等量代换即可得证；（2）连接，根据同弧所对的圆周角相等，可得，进而根据正切值以及已知条件可得的长，勾股定理即可求得，进而即可求得圆的半径．【详解】（1）连接，如图，是的切线，，，，，，，．（2）连接是的直径，，，，，，，，，．即的半径为．18．（2021·山东济南·中考真题）计算：．【答案】6【分析】根据负指数幂、零次幂及三角函数值可进行求解．【详解】解：原式=．