考点19特殊平行四边形（解析版）-2022年数学中考一轮复习考点透析（华师大版）

这是一份考点19特殊平行四边形（解析版）-2022年数学中考一轮复习考点透析（华师大版），共28页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

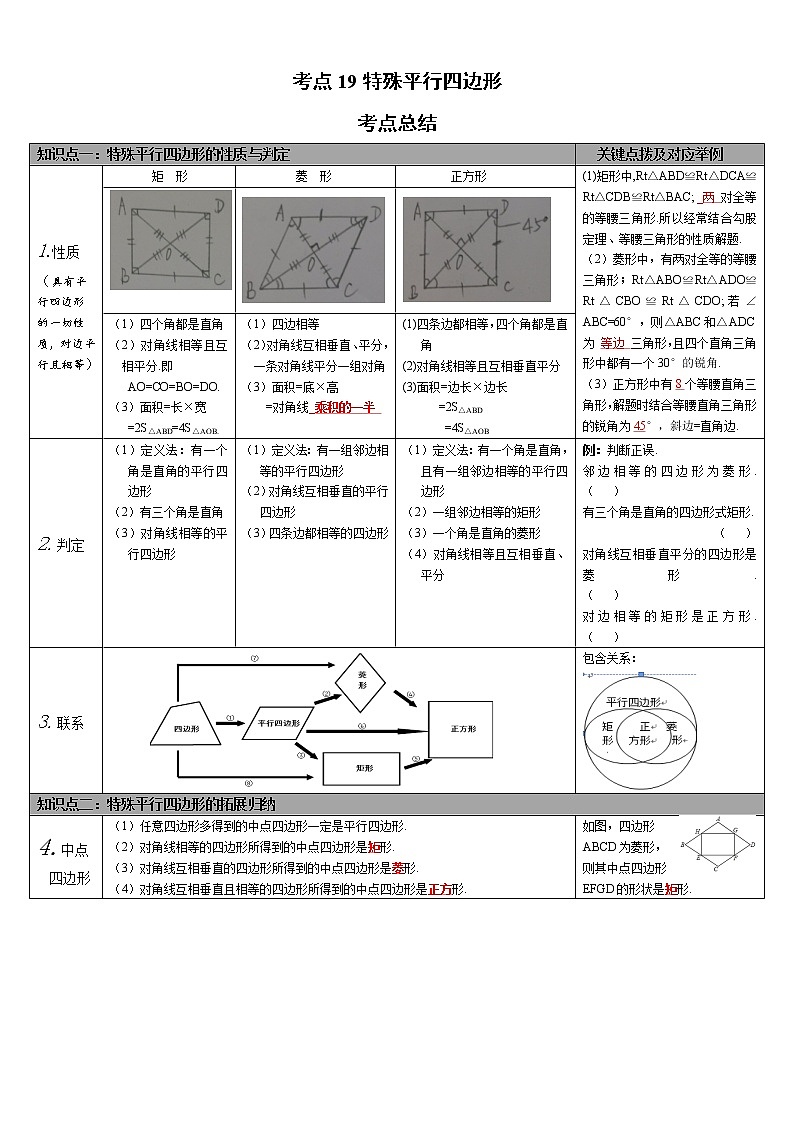
考点19特殊平行四边形
考点总结
知识点一：特殊平行四边形的性质与判定
关键点拨及对应举例
1.性质
（具有平行四边形的一切性质，对边平行且相等）
矩 形
菱 形
正方形
(1)矩形中,Rt△ABD≌Rt△DCA≌Rt△CDB≌Rt△BAC; _两 对全等的等腰三角形.所以经常结合勾股定理、等腰三角形的性质解题.
（2）菱形中，有两对全等的等腰三角形；Rt△ABO≌Rt△ADO≌Rt△CBO≌Rt△CDO;若∠ABC=60°，则△ABC和△ADC为 等边 三角形，且四个直角三角形中都有一个30°的锐角.
（3）正方形中有8个等腰直角三角形，解题时结合等腰直角三角形的锐角为45°，斜边=直角边.



（1）四个角都是直角
（2）对角线相等且互相平分.即
AO=CO=BO=DO.
（3）面积=长×宽
=2S△ABD=4S△AOB.
（1）四边相等
（2）对角线互相垂直、平分，一条对角线平分一组对角
（3）面积=底×高
=对角线_乘积的一半
(1)四条边都相等，四个角都是直角
(2)对角线相等且互相垂直平分
(3)面积=边长×边长
=2S△ABD
=4S△AOB
2.判定
（1）定义法：有一个角是直角的平行四边形
（2）有三个角是直角
（3）对角线相等的平行四边形
（1）定义法：有一组邻边相等的平行四边形
（2）对角线互相垂直的平行四边形
（3）四条边都相等的四边形
（1）定义法：有一个角是直角，且有一组邻边相等的平行四边形
（2）一组邻边相等的矩形
（3）一个角是直角的菱形
（4）对角线相等且互相垂直、平分
例：判断正误.
邻边相等的四边形为菱形.（ ）
有三个角是直角的四边形式矩形.
（ ）
对角线互相垂直平分的四边形是菱形. （ ）
对边相等的矩形是正方形.（ ）
3.联系

包含关系：

知识点二：特殊平行四边形的拓展归纳
4.中点四边形
（1）任意四边形多得到的中点四边形一定是平行四边形.
（2）对角线相等的四边形所得到的中点四边形是矩形.
（3）对角线互相垂直的四边形所得到的中点四边形是菱形.
（4）对角线互相垂直且相等的四边形所得到的中点四边形是正方形.
如图，四边形ABCD为菱形，则其中点四边形EFGD的形状是矩形.
5.特殊四边形中的解题模型
（1）矩形：如图①，E为AD上任意一点，EF过矩形中心O，则△AOE≌△COF,S1=S2.
（2）正方形:如图②，若EF⊥MN，则EF=MN;如图③，P为AD边上任意一点，则PE+PF=AO. （变式：如图④，四边形ABCD为矩形，则PE+PF的求法利用面积法，需连接PO.）




图① 图② 图③ 图④


真题演练
一、单选题
1．（2021·山东日照·中考真题）下列命题：①的算术平方根是2；②菱形既是中心对称图形又是轴对称图形；②天气预报说明天的降水概率是，则明天一定会下雨；④若一个多边形的各内角都等于，则它是正五边形，其中真命题的个数是（　　）
A．0 B．1 C．2 D．3
【答案】B
【分析】
利用算术平方根的定义、菱形的对称性、概率的意义及多边形的内角和等知识分别判断后即可确定正确的选项．
【详解】
解：①的算术平方根是，故原命题错误，是假命题；
②菱形既是中心对称图形又是轴对称图形，正确，是真命题；
②天气预报说明天的降水概率是，则明天下雨可能性很大，但不确定是否一定下雨，故原命题错误，是假命题；
④若一个多边形的各内角都等于，各边也相等，则它是正五边形，故原命题错误，是假命题；
真命题有1个，
故选：B．
2．（2021·山东潍坊·中考真题）若菱形两条对角线的长度是方程x2﹣6x+8＝0的两根，则该菱形的边长为（ ）
A． B．4 C．25 D．5
【答案】A
【分析】
先求出方程的解，即可得到，根据菱形的性质求出和 ，根据勾股定理求出即可．
【详解】
解：解方程，得，
即，
∵四边形是菱形，
∴，
由勾股定理得，
即菱形的边长为，


故选：．
3．（2021·山东潍坊·中考真题）古希腊数学家欧几里得在《几何原本》中记载了用尺规作某种六边形的方法，其步骤是：①在⊙O上任取一点A，连接AO并延长交⊙O于点B；②以点B为圆心，BO为半径作圆弧分别交⊙O于C，D两点；③连接CO，DO并延长分别交⊙O于点E，F；④顺次连接BC，CF，FA，AE，ED，DB，得到六边形AFCBDE．连接AD，EF，交于点G，则下列结论错误的是 ．

A．△AOE的内心与外心都是点G B．∠FGA＝∠FOA
C．点G是线段EF的三等分点 D．EF＝AF
【答案】D
【分析】
证明△AOE是等边三角形，EF⊥OA，AD⊥OE，可判断A；．证明∠AGF=∠AOF=60°，可判断B；证明FG=2GE，可判断C；证明EF=AF，可判断D．
【详解】
解：如图，

在正六边形AEDBCF中，∠AOF=∠AOE=∠EOD=60°，
∵OF=OA=OE=OD，
∴△AOF，△AOE，△EOD都是等边三角形，
∴AF=AE=OE=OF，OA=AE=ED=OD，
∴四边形AEOF，四边形AODE都是菱形，
∴AD⊥OE，EF⊥OA，
∴△AOE的内心与外心都是点G，故A正确，
∵∠EAF=120°，∠EAD=30°，
∴∠FAD=90°，
∵∠AFE=30°，
∴∠AGF=∠AOF=60°，故B正确，
∵∠GAE=∠GEA=30°，
∴GA=GE，
∵FG=2AG，
∴FG=2GE，
∴点G是线段EF的三等分点，故C正确，
∵AF=AE，∠FAE=120°，
∴EF=AF，故D错误，
故答案为：D．
4．（2021·山东威海·中考真题）如图，在平行四边形中，，．连接AC，过点B作，交DC的延长线于点E，连接AE，交BC于点F．若，则四边形ABEC的面积为（ ）

A． B． C．6 D．
【答案】B
【分析】
先证明四边形ABEC为矩形，再求出AC，即可求出四边形ABEC的面积．
【详解】
解：∵四边形ABCD是平行四边形，
∴AB∥CD，AB=CD=2，BC=AD=3，∠D=∠ABC，
∵，
∴四边形ABEC为平行四边形，
∵，
∴，
∵∠AFC=∠ABF+∠BAF，
∴∠ABF=∠BAF，
∴AF=BF，
∴2AF=2BF，
即BC=AE，
∴平行四边形ABEC是矩形，
∴∠BAC=90°，
∴,
∴矩形ABEC的面积为．
故选：B
5．（2021·山东枣庄·中考真题）如图，四边形是菱形，对角线，相交于点，，，点是上一动点，点是的中点，则的最小值为（ ）

A． B． C．3 D．
【答案】A
【分析】
连接，先根据两点之间线段最短可得当点共线时，取得最小值，再根据菱形的性质、勾股定理可得，然后根据等边三角形的判定与性质求出的长即可得．
【详解】
解：如图，连接，

由两点之间线段最短得：当点共线时，取最小值，最小值为，
四边形是菱形，，，
，
，
，
是等边三角形，
点是的中点，
，
，
即的最小值为，
故选：A．
6．（2021·山东泰安·中考真题）如图，在平行四边形中，E是的中点，则下列四个结论：①；②若，，则；③若，则；④若，则与全等．其中正确结论的个数为（ ）

A．1个 B．2个 C．3个 D．4个
【答案】D
【分析】
依次分析各选项，进行推理论证即可；其中①可通过证明，进一步转换后可以得到结论，②可先得到该平行四边形是矩形，利用矩形的性质等得到MN垂直平分BC，即可完成求证，③可以先证明两个三角形的共线边上的高的关系，再利用三角形面积公式即可完成证明，④可以先证明后可进一步证明，即可完成求证．
【详解】
解：∵平行四边形中，E是的中点，
∴，，，
∴,,
∴,
∴，
∴，
故①正确；
若，
则平行四边形是矩形，
由矩形的对角线相等，而点E是矩形的对角线的交点可知，
E点到B、C两点的距离相等，
∴E点在BC的垂直平分线上，
由，可得BN=CN，
所以N点是BC的中点，
∴MN垂直平分BC，
∴，
故②正确；
若，则BN=2CN，
如图1，分别过D、E两点向BC作垂线，垂足分别为Q点和P点，
∵E点是BD中点，
∴DQ=2EP，
∵，

∴，
故③正确；
若，
因为，
所以，
分别过N、C两点向AD作垂线，垂足分别为H、K，
由平行线间的距离处处相等可知：NH=CK，
∴，
∴，
∴,
∴，
又∵，
∴,
故④正确；
故选：D．

7．（2021·山东·青岛大学附属中学二模）如图，在矩形中，为边上一点，把沿翻折，使点恰好落在边上的点处，，，则的长为（ ）

A． B．1
C． D．
【答案】A
【分析】
先证得△ABF∽△FCE，再根据矩形的性质及翻折变换的性质推出BC=AD=AF=4，从而利用勾股定理求得BF=2，进而结合线段之间的和差关系利用相似三角形的性质进行求解即可．
【详解】
解：∵四边形ABCD是矩形，
∴∠B=∠C=∠D=90°，
又△ADE沿AE翻折得到△AFE，
∴∠D=∠AFE=90°，
∵∠BAF+∠AFB=90°，∠EFC+∠AFB=90°，
∴∠BAF=∠EFC，
∴△ABF∽△FCE；
∵AB=，AD=4，
∴BC=AD=AF=4，
在Rt△ABF中，
，
∴CF=BC-BF=4-2=2，
又∵△ABF∽△FCE，
∴，即，
解得：，
故选择：A
8．（2021·山东·济宁学院附属中学二模）如图，矩形纸片，，，E为边D上一点，将沿所在的直线折叠，点C恰好落在边上的点F处，过点F作，垂足为点M，取的中点N，连接，则=（　　）．

A．5 B．6 C． D．
【答案】A
【分析】
连接，，可求得为的中点，根据中位线的性质可得，勾股定理求得即可．
【详解】
解：连接，

由折叠的性质可得，
又∵
∴点在线段上，
又∵
∴
∴
又∵的中点N
∴为的中位线
∴
在中，
∴
故选A
9．（2021·山东省诸城市树一中学三模）如图，菱形的边长为2，，分别以点和点为圆心，大于的长为半径作弧，两弧相交于，两点，直线交于点，连接，则的长为（ ）

A．2 B．3
C． D．
【答案】D
【分析】
连接BE，由垂直平分线的性质和等腰直角三角形的性质，得BE=AE=， 再得∠EBC=90°，利用勾股定理即可求出CE的长度．
【详解】
解：连接BE，如图：
由题意可知，MN垂直平分AB，
∴AE=BE，
∴，
∴∠AEB=90°，
在等腰直角三角形ABE中，AB=2，
∴BE=AE=，
∵四边形ABCD为菱形，
∴AD∥BC，
∴∠EBC=∠AEB=90°，
在Rt△BCE中，由勾股定理，则
；
故选D．

10．（2021·山东枣庄·一模）如图，在矩形ABCD中，O为AC中点，交AB于E，点G是AE中点且∠AOG＝30°，下列结论：（1）DC＝3OG；（2）OG＝BC；（3）等边三角形；（4）S△AOE＝S矩形ABCD，正确的有（ ）

A．1个 B．2个 C．3个 D．4个
【答案】C
【分析】
根据矩形的性质、等边三角形的判定、勾股定理逐一判断即可；
【详解】
∵点G是AE中点，，
∴，
∵∠AOG＝30°，
∴，，
∴等边三角形，故（3）正确；
设，则，
由勾股定理得，，
∵O为AC中点，
∴，
在中，，
∴，
由勾股定理得，，
∵四边形ABCD是矩形，
∴，
∴DC＝3OG，故（1）正确；
∵，，
∴，故（2）错误；
∵，
，
∴，故（4）正确；
综上所述，正确的结论有（1）（3）（4）；
故答案选C．

二、填空题
11．（2021·山东泰安·中考真题）如图，将矩形纸片折叠（），使落在上，为折痕，然后将矩形纸片展开铺在一个平面上，E点不动，将边折起，使点B落在上的点G处，连接，若，，则的长为________．

【答案】
【分析】
根据矩形的性质和正方形的性质，证明，从而，又因为，代入求解即可．
【详解】
解：∵四边形是矩形,，
∴,,,且四边形是正方形，
∴，
∴，
又∵，
∴，
∴
又∵（折叠，
∴，, ，
设,则，
∴ ，
又∵是正方形对角线，
∴ ，
∴ ，
∴ ，
∴ ，解得：，即 ，
∴．
故答案为：
12．（2021·山东临沂·中考真题）数学知识在生产和生活中被广泛应用，下列实例所应用的最主要的几何知识，说法正确的是___（只填写序号）．
①射击时，瞄准具的缺口、准星和射击目标在同一直线上，应用了“两点确定一条直线”；
②车轮做成圆形，应用了“圆是中心对称图形”；
③学校门口的伸缩门由菱形而不是其他四边形组成，应用了“菱形的对角线互相垂直平分”；
④地板砖可以做成矩形，应用了“矩形对边相等”．

【答案】①
【分析】
根据直线的性质，圆的性质，特殊四边形的性质分别判断即可．
【详解】
解：①射击时，瞄准具的缺口、准星和射击目标在同一直线上，应用了“两点确定一条直线”，故正确；
②车轮做成圆形，应用了“同圆的半径相等”，故错误；
③学校门口的伸缩门由菱形而不是其他四边形组成，应用了“菱形的四边相等”，故错误；
④地板砖可以做成矩形，应用了“矩形的四个角是直角，可以密铺”，故错误；
故答案为：①．
13．（2021·山东青岛·中考真题）已知正方形的边长为3，为上一点，连接并延长，交的延长线于点，过点作，交于点，交于点，为的中点，为上一动点，分别连接，．若，则的最小值为__________．

【答案】
【分析】
由正方形的性质，可得A点与C点关于BD对称，则有MN +CM=MN+AM≥AN，所以当A、M、N三点共线时，MN+CM的值最小为AN，先证明△DCG~△FCE，再由，可得，分别求出DE=1，CE=2，CF=6，即可求出AN．
【详解】
解：∵四边形ABCD是正方形，
∴A点与C点关于BD对称，
∴CM=AM，
∴MN+CM=MN+AM≥AN，
∴当A、M、N三点共线时，MN+CM的值最小，
∵AD∥CF，
∴∠DAE=∠F，
∵∠DAE+∠DEH=90°，
∵DG⊥AF，
∴∠CDG+∠DEH=90°，
∴∠DAE=∠CDG，
∴∠CDG=∠F，
∴△DCG~△FCE，
∵，
∴ ，
∵正方形边长为3，
∴CF=6，
∵AD∥CF，
，
∴DE=1，CE=2，
在Rt△CEF中，EF2=CE2+CF2，
∴ ，
∵N是EF的中点，
，
在Rt△ADE中，EA2=AD2+DE2，
∴ ，
∴ ，
∴MN+MC的最小值为 ．
故答案为：．
14．（2021·山东日照·中考真题）如图，在矩形中，，，点从点出发，以的速度沿边向点运动，到达点停止，同时，点从点出发，以的速度沿边向点运动，到达点停止，规定其中一个动点停止运动时，另一个动点也随之停止运动．当为_____时，与全等．

【答案】2或
【分析】
可分两种情况：①得到，，②得到，，然后分别计算出的值，进而得到的值．
【详解】
解：①当，时，，
，
，
，
，解得：，
，
，
解得：；
②当，时，，
，
，
，解得：，
，
，
解得：，
综上所述，当或时，与全等，
故答案为：2或．
15．（2021·山东淄博·中考真题）两张宽为的纸条交叉重叠成四边形，如图所示．若，则对角线上的动点到三点距离之和的最小值是__________．

【答案】
【分析】
由题意易得四边形是菱形，过点D作DE⊥BC于点E，连接AC，交BD于点O，易得，，然后根据勾股定理可得，则，，进而可得，要使为最小，即的值为最小，则可过点A作AM⊥AP，且使，连接BM，最后根据“胡不归”问题可求解．
【详解】
解：∵纸条的对边平行，即，
∴四边形是平行四边形，
∵两张纸条的宽度都为，
∴，
∴，
∴四边形是菱形，
过点D作DE⊥BC于点E，连接AC，交BD于点O，如图所示：

∴，
∴，
∴，
∵，，
∴，，
∴，
∴，
∴，，
∴，
过点A作AM⊥AP，且使，连接BM，如图所示：

∴，
要使的值为最小，则需满足为最小，根据三角不等关系可得：，所以当B、P、M三点共线时，取最小，即为BM的长，如图所示：

∴，
∴，
∴的最小值为，即的最小值为；
故答案为．

三、解答题
16．（2021·山东滨州·中考真题）如图，矩形ABCD的对角线AC、BD相交于点O，，．
（1）求证：四边形AOBE是菱形；
（2）若，，求菱形AOBE的面积．

【答案】（1）证明过程见解答；（2）
【分析】
（1）根据BE∥AC，AE∥BD，可以得到四边形AOBE是平行四边形，然后根据矩形的性质，可以得到OA=OB，由菱形的定义可以得到结论成立；
（2）根据∠AOB=60°，AC=4，可以求得菱形AOBE边OA上的高，然后根据菱形的面积=底×高，代入数据计算即可．
【详解】
解：（1）证明：∵BE∥AC，AE∥BD，
∴四边形AOBE是平行四边形，
∵四边形ABCD是矩形，
∴AC=BD，OA=OC=AC，OB=OD=BD，
∴OA=OB，
∴四边形AOBE是菱形；
（2）解：作BF⊥OA于点F，

∵四边形ABCD是矩形，AC=4，
∴AC=BD=4，OA=OC=AC，OB=OD=BD，
∴OA=OB=2，
∵∠AOB=60°，
∴BF=OB•sin∠AOB=，
∴菱形AOBE的面积是：OA•BF==．
17．（2021·山东枣庄·中考真题）如图1，对角线互相垂直的四边形叫做垂美四边形．
（1）概念理解：如图2，在四边形中，，，问四边形是垂美四边形吗？请说明理由；
（2）性质探究：如图1，垂美四边形的对角线，交于点．猜想：与有什么关系？并证明你的猜想．
（3）解决问题：如图3，分别以的直角边和斜边为边向外作正方形和正方形，连结，，．已知，，求的长．

【答案】（1）四边形是垂美四边形，理由见解析；（2），证明见解析；（3）．
【分析】
（1）连接，先根据线段垂直平分线的判定定理可证直线是线段的垂直平分线，再根据垂美四边形的定义即可得证；
（2）先根据垂美四边形的定义可得，再利用勾股定理解答即可；
（3）设分别交于点，交于点，连接，先证明，得到，再根据角的和差可证，即，从而可得四边形是垂美四边形，然后结合（2）的结论、利用勾股定理进行计算即可得．
【详解】
证明：（1）四边形是垂美四边形，理由如下：
如图，连接，

∵，
∴点在线段的垂直平分线上，
∵，
∴点在线段的垂直平分线上，
∴直线是线段的垂直平分线，即，
∴四边形是垂美四边形；
（2）猜想，证明如下：
∵四边形是垂美四边形，
∴，
∴，
由勾股定理得：，
，
∴；
（3）如图，设分别交于点，交于点，连接，

∵四边形和四边形都是正方形，
∴，
∴，即，
在和中，，
∴，
∴，
又∵，，
∴，
∴，即，
∴四边形是垂美四边形，
由（2）得：，
∵是的斜边，且，，
∴，，
在中，，
在中，，
∴，
解得或（不符题意，舍去），
故的长为．
18．（2021·山东淄博·中考真题）已知：在正方形的边上任取一点，连接，一条与垂直的直线（垂足为点）沿方向，从点开始向下平移，交边于点．

（1）当直线经过正方形的顶点时，如图1所示．求证：；
（2）当直线经过的中点时，与对角线交于点，连接，如图2所示．求的度数；
（3）直线继续向下平移，当点恰好落在对角线上时，交边于点，如图3所示．设，求与之间的关系式．
【答案】（1）见详解；（2）；（3）
【分析】
（1）由题意易得，进而可得，则有，然后问题可求证；
（2）连接AQ，过点Q作QM⊥AD于点M，并延长MQ，交BC于点N，由题意易得AQ=FQ，∠ADB=45°，则有QM=MD，进而可得证，然后可得，则问题可求解；
（3）过点D作DH∥EG，交AB于点H，由题意易证四边形HEGD是平行四边形，则有，进而可得，然后可得，则问题可求解．
【详解】
（1）证明：∵四边形是正方形，
∴，
∵AF⊥ED，
∴，
∴，
∴，
∴，
∴；
（2）解：连接AQ，过点Q作QM⊥AD于点M，并延长MQ，交BC于点N，如图所示：

∵点P是AF的中点，AF⊥EQ，
∴，
∵四边形是正方形，
∴，
∴四边形MNCD是矩形，△MDQ是等腰直角三角形，
∴，
∴，
∴，
∴，
∵，
∴，即，
∴是等腰直角三角形，
∴；
（3）过点D作DH∥EG，交AB于点H，如图所示：

∴四边形HEGD是平行四边形，
∴，
∵AF⊥EG，
∴AF⊥HD，
由（1）中结论可得，
∵，
∴，，
∴，
∵，
∴，
∴，
∴，
∴，
∴与之间的关系式为．
19．（2021·山东潍坊·中考真题）如图，在直角坐标系中，O为坐标原点，抛物线的顶点为（2，﹣），抛物线与轴的一个交点为A（4，0），点B（2，），点C与点B关于y轴对称．

（1）判断点C是否在该抛物线上，并说明理由；
（2）顺次连接AB，BC，CO，判断四边形的形状并证明；
（3）设点P是抛物线上的动点，连接PA、PC、AC，△PAC的面积S随点P的运动而变化；请探究的大小变化并填写表格①④处的内容；在当S的值为②时，求点P的横坐标的值．
直线的函数表达式
取的一个特殊值
满足条件的点的个数
的可能取值范围
①　　
6
4个
③　　
②　　
3个

10
2个
④　　
【答案】（1）点在该抛物线上；证明见解答；（2）四边形是菱形；（3）①；②；③；④．当=时，点P的横坐标为或1或．
【分析】
（1）运用待定系数法，设抛物线解析式为，将代入，即可求得抛物线解析式，当时，，故点在该抛物线上；
（2）根据，，，的纵坐标相等可判断轴，再由，可判断四边形是平行四边形，再运用两点间距离公式求出，运用菱形的判定定理即可．
（3）①设，将，坐标代入即可求出直线的函数表达式；②当点在直线下方的抛物线上时，如图2，设，过点作轴交直线于点，则，根据满足条件的点有3个，可得在直线下方的抛物线上只有1个点，即的值最大，再利用二次函数最值性质即可得出答案；③由满足条件的点有3个，结合②即可得出答案；④满足条件的点只有2个，而在直线上方的抛物线上一定有2个点，满足，故在直线下方的抛物线上没有点，满足，结合②即可得出答案．
【详解】
解：（1）设抛物线解析式为，将代入，
得：，
解得：，
抛物线解析式为，
点，与点关于轴对称，
，，
当时，，
点在该抛物线上；
（2）四边形是菱形．

证明：，，，，
轴，，
，
，
，
四边形是平行四边形，
，
，
四边形是菱形．
（3）①设直线的函数表达式为，
，，，
，
解得：，
直线的函数表达式为；
故答案为：；
②当点在直线下方的抛物线上时，如图2，

设，过点作轴交直线于点，
则，
，
满足条件的点有3个，
在直线下方的抛物线上只有1个点，即的值最大，
，
当时，取得最大值，此时点，
故答案为：；
当P点在直线AC上方时，
∴，
当=时，即：，解得：，
综上所述：当=时，点P的横坐标为或1或．
③由②知，当时，在直线下方的抛物线上有2个点，满足，
在直线上方的抛物线上一定有2个点，满足，
满足条件的点有4个，符合题意．
故答案为：；
④满足条件的点只有2个，而在直线上方的抛物线上一定有2个点，满足，
在直线下方的抛物线上没有点，满足，
由②知，当时，在直线下方的抛物线上没有点，满足，符合题意．
故答案为：．