

考点04二次根式(解析版)-2022年数学中考一轮复习考点透析(华师大版)
展开考点04二次根式
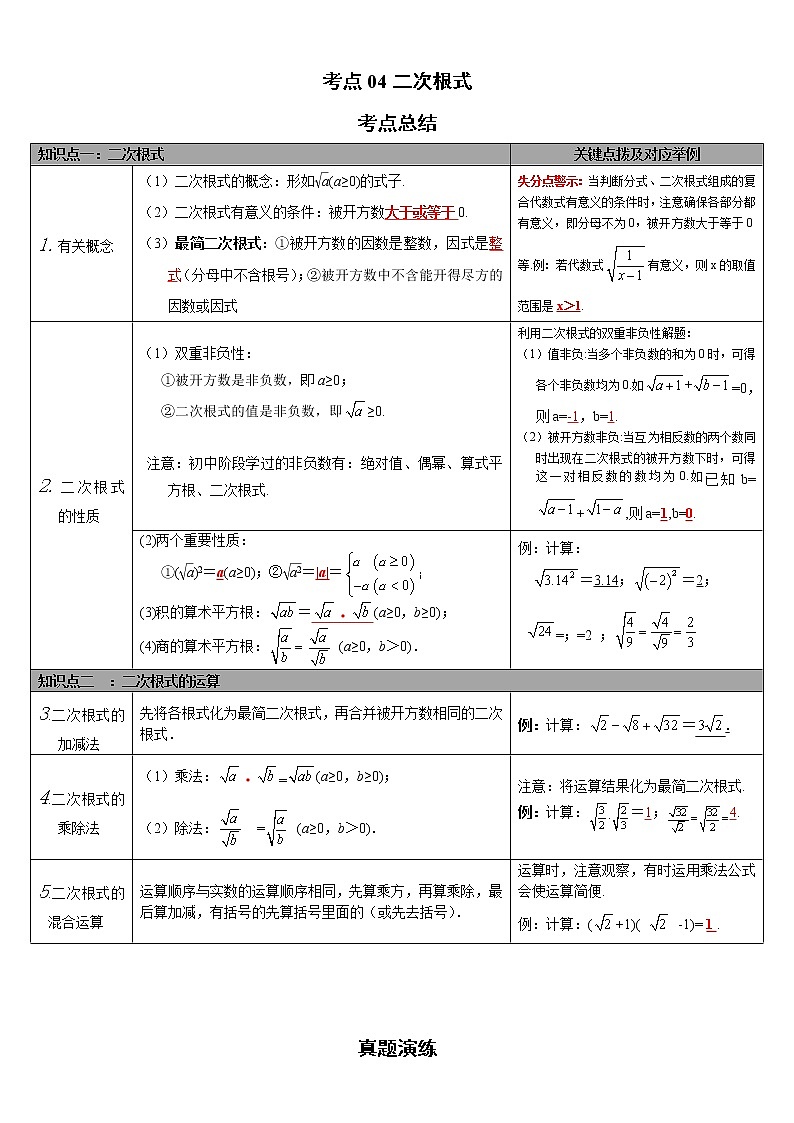
考点总结
知识点一:二次根式 | 关键点拨及对应举例 | |
1.有关概念 | (1)二次根式的概念:形如(a≥0)的式子. (2)二次根式有意义的条件:被开方数大于或等于0. (3)最简二次根式:①被开方数的因数是整数,因式是整式(分母中不含根号);②被开方数中不含能开得尽方的因数或因式 | 失分点警示:当判断分式、二次根式组成的复合代数式有意义的条件时,注意确保各部分都有意义,即分母不为0,被开方数大于等于0等.例:若代数式有意义,则x的取值范围是x>1. |
2.二次根式的性质 | (1)双重非负性: ①被开方数是非负数,即a≥0; ②二次根式的值是非负数,即≥0.
注意:初中阶段学过的非负数有:绝对值、偶幂、算式平方根、二次根式. | 利用二次根式的双重非负性解题: (1)值非负:当多个非负数的和为0时,可得各个非负数均为0.如+=0,则a=-1,b=1. (2)被开方数非负:当互为相反数的两个数同时出现在二次根式的被开方数下时,可得这一对相反数的数均为0.如已知b=+,则a=1,b=0. |
(2)两个重要性质: ①()2=a(a≥0);②=|a|=; (3)积的算术平方根:=·(a≥0,b≥0); (4)商的算术平方根: (a≥0,b>0). | 例:计算: =3.14;=2; =;=2 ; | |
知识点二 :二次根式的运算 | ||
3.二次根式的加减法 | 先将各根式化为最简二次根式,再合并被开方数相同的二次根式. | 例:计算:=. |
4.二次根式的乘除法 | (1)乘法:·=(a≥0,b≥0); (2)除法: = (a≥0,b>0). | 注意:将运算结果化为最简二次根式. 例:计算:=1;4. |
5.二次根式的混合运算 | 运算顺序与实数的运算顺序相同,先算乘方,再算乘除,最后算加减,有括号的先算括号里面的(或先去括号). | 运算时,注意观察,有时运用乘法公式会使运算简便. 例:计算:(+1)( -1)= 1 . |
真题演练
一、单选题
1.(2021·山东潍坊·中考真题)下列运算正确的是 .
A. B. C. D.
【答案】A
【分析】
根据完全平方公式、负数指数幂、分式的化简、根式的化简分别计算解答即可.
【详解】
解:A、,选项运算正确;
B、,选项运算错误;
C、是最简分式,选项运算错误;
D、,选项运算错误;
故选:A.
2.(2021·山东东营·中考真题)下列运算结果正确的是( )
A. B.
C. D.
【答案】B
【分析】
根据合并同类项法则、完全平方公式、积的乘方的运算法则、二次根式的运算法则依次计算各项后即可解答.
【详解】
选项A,和不是同类项,不能够合并,选项A错误;
选项B,根据完全平方公式可得,选项B正确;
选项C,根据积的乘方的运算法则可得,选项C错误;
选项D,与不能够合并,选项D错误.
故选B.
3.(2021·山东临沂·中考真题)如图,点,都在格点上,若,则的长为( )
A. B. C. D.
【答案】B
【分析】
利用勾股定理求出AB,再减去BC可得AC的长.
【详解】
解:由图可知:
AB==,
∵BC=,
∴AC=AB-BC==,
故选B.
4.(2020·山东日照·中考真题)下列各式中,运算正确的是( )
A.x3+x3=x6 B.x2•x3=x5
C.(x+3)2=x2+9 D.﹣=
【答案】B
【分析】
由题意根据合并同类项的法则:把同类项的系数相加,所得结果作为系数,字母和字母的指数不变;同底数幂的乘法法则,底数不变,指数相加;完全平方公式:(a±b)2=a2±2ab+b2;以及二次根式的减法运算法则逐项分析即可.
【详解】
解:A、x3+x3=2x3,故选项A不符合题意;
B、x2•x3=x5计算正确,故选项B符合题意;
C、(x+3)2=x2+6x+9,故选项C不符合题意;
D、二次根式与不是同类二次根式故不能合并,故选项D不符合题意.
故选:B.
5.(2020·山东菏泽·中考真题)函数的自变量的取值范围是( )
A. B.且 C. D.且
【答案】D
【分析】
由分式与二次根式有意义的条件得函数自变量的取值范围.
【详解】
解:由题意得:
解得:且
故选D.
6.(2020·山东聊城·中考真题)计算的结果正确的是( ).
A.1 B. C.5 D.9
【答案】A
【分析】
利用二次根式的乘除法则计算即可得到结果.
【详解】
解:
,
故选:A.
7.(2020·山东济宁·中考真题)下列各式是最简二次根式的是( )
A. B. C. D.
【答案】A
【分析】
根据最简二次根式的定义即可求出答案.
【详解】
解:A、是最简二次根式,故选项正确;
B、=,不是最简二次根式,故选项错误;
C、,不是最简二次根式,故选项错误;
D、,不是最简二次根式,故选项错误;
故选A.
8.(2021·山东兰陵·一模)实数,在数轴上对应的点的位置如图所示,化简的结果是( )
A. B. C. D.
【答案】A
【分析】
根据数轴确定a的取值范围,根据绝对值的性质,二次根式的性质化简即可.
【详解】
解:由数轴可知,a<0<b,
∴a-b<0
∴;
故选:A
9.(2021·山东滨城·模拟预测)式子有意义,则实数的取值范围是( )
A. B. C.且 D.且
【答案】C
【分析】
根据分式和二次根式有意义的条件,判断实数的取值范围
【详解】
有意义
解得:且
故选C
10.(2021·山东诸城·二模)下列计算正确的是( )
A. B. C. D.
【答案】A
【分析】
根据分式的化简,二次根式的加减运算,负指数幂逐项分析即可.
【详解】
A. ,符合题意;
B. ,不符合题意;
C. ,不符合题意;
D.,不符合题意.
故选A.
二、填空题
11.(2021·山东青岛·中考真题)计算:__________.
【答案】5
【分析】
先运用乘法分配律展开,再利用二次根式的乘法法则计算即可,
【详解】
解:,
12.(2021·山东聊城·中考真题)计算:=_______.
【答案】4
【分析】
根据二次根式的运算法则,先算乘法,再算加减法,即可.
【详解】
解:原式=
=
=
=4.
故答案是:4.
13.(2021·山东烟台·中考真题)若在实数范围内有意义,则的取值范围为__________.
【答案】x≤2
【分析】
二次根式的被开方数大于等于零,据此解答.
【详解】
解:依题意得 2-x≥0
解得 x≤2.
故答案为:x≤2.
14.(2021·山东日照·中考真题)若式子有意义,则x的取值范围是___.
【答案】且
【详解】
∵式子在实数范围内有意义,
∴x+1≥0,且x≠0,
解得:x≥-1且x≠0.
故答案为x≥-1且x≠0.
15.(2021·山东威海·中考真题)计算的结果是____________________.
【答案】
【分析】
根据二次根式的四则运算法则进行运算即可求解.
【详解】
解:原式
,
故答案为:.
三、解答题
16.(2021·山东淄博·中考真题)先化简,再求值:,其中.
【答案】,2
【分析】
先对分式进行化简,然后再代入进行二次根式的运算即可.
【详解】
解:原式=,
把代入得:原式=.
17.(2021·山东菏泽·中考真题)计算:.
【答案】0
【分析】
根据零指数幂,绝对值的化简,负整数指数幂,特殊角的函数值计算即可
【详解】
=1+3
=0.
18.(2021·山东临沂·中考真题)计算.
【答案】
【分析】
化简绝对值,同时利用平方差公式计算,最后合并.
【详解】
解:
=
=
=
考点04整式运算(解析版)-2022年数学中考一轮复习考点透析(北京版): 这是一份考点04整式运算(解析版)-2022年数学中考一轮复习考点透析(北京版),共11页。试卷主要包含了单项式及多项式,整式混合运算,幂的运算,完全平方公式及其几何背景,平方差公式及其几何背景等内容,欢迎下载使用。
考点04因式分解(解析版)-2022年数学中考一轮复习考点透析(青岛版): 这是一份考点04因式分解(解析版)-2022年数学中考一轮复习考点透析(青岛版),共9页。试卷主要包含了因式分解的概念,因式分解的方法等内容,欢迎下载使用。
考点03分式(解析版)-2022年数学中考一轮复习考点透析(华师大版): 这是一份考点03分式(解析版)-2022年数学中考一轮复习考点透析(华师大版),共10页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。












