

所属成套资源:冀教版2022年数学中考一轮复习考点透析
考点01 实数(解析版)-2022年数学中考一轮复习考点透析(冀教版)
展开
这是一份考点01 实数(解析版)-2022年数学中考一轮复习考点透析(冀教版),共10页。试卷主要包含了数轴,相反数,倒数,绝对值,按照定义分类,科学记数法,近似数,平方根等内容,欢迎下载使用。
1.数轴:规定了原点、单位长度和正方向的直线叫做数轴.数轴上所有的点与全体实数一一对应.
2.相反数:只有符号不同,而绝对值相同的两个数称为互为相反数,若a、b互为相反数,则a+b=0.
3.倒数:1除以一个不等于零的实数所得的商,叫做这个数的倒数.若a、b互为倒数,则ab=1.
4.绝对值:数轴上表示数a的点与原点的距离,记作 |a|.
5.(1)按照定义分类
(2)按照正负分类
注意:0既不属于正数,也不属于负数.另外,在理解无理数时,要注意“无限不循环”,归纳起来有四类:
(1)开方开不尽的数,如,等;
(2)有特定意义的数,如圆周率π,或化简后含有π的数,如等;
(3)有特定结构的数,如0.101 001 000 1…等;
(4)某些三角函数,如sin60°等.
6.科学记数法:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.当原数绝对值大于10时,写成a×10n的形式,其中1≤|a|<10,n等于原数的整数位数减1;当原数绝对值小于1时,写成a×10−n的形式,其中1≤|a|<10,n等于原数左边第一个非零的数字前的所有零的个数(包括小数点前面的零).
7.近似数:近似数与准确数的接近程度通常用精确度来表示,近似数一般由四舍五入取得,四舍五入到哪一位,就说这个近似数精确到哪一位.
8.平方根:(1)算术平方根的概念:若x2=a(x>0),则正数x叫做a的算术平方根.
(2)平方根的概念:若x2=a,则x叫做a的平方根.
(3)表示:a的平方根表示为,a的算术平方根表示为.
(4)
9.立方根:(1)定义:若x3=a,则x叫做a的立方根.
(2)表示:a的立方根表示为.
(3).
10.数的乘方:求 QUOTE n个相同因数a的积的运算叫做乘方,乘方的结果叫幂.在an中,a叫底数,n叫指数.
11.实数的运算:
(1)有理数的运算定律在实数范围内都适用,常用的运算定律有加法结合律 、加法交换律 、乘法交换律 、乘法结合律、 乘法分配律.
(2)运算顺序:先算乘方(开方),再算乘除,最后算加减;有括号的先算括号里面的.
12.指数,负整数指数幂:a≠0,则a0=1;若a≠0,n为正整数,则.
13.数的大小比较常用以下几种方法:数轴比较法、差值比较法、绝对值比较法、乘方比较法、中间值比较法等等.
真题演练
一.选择题(共10小题)
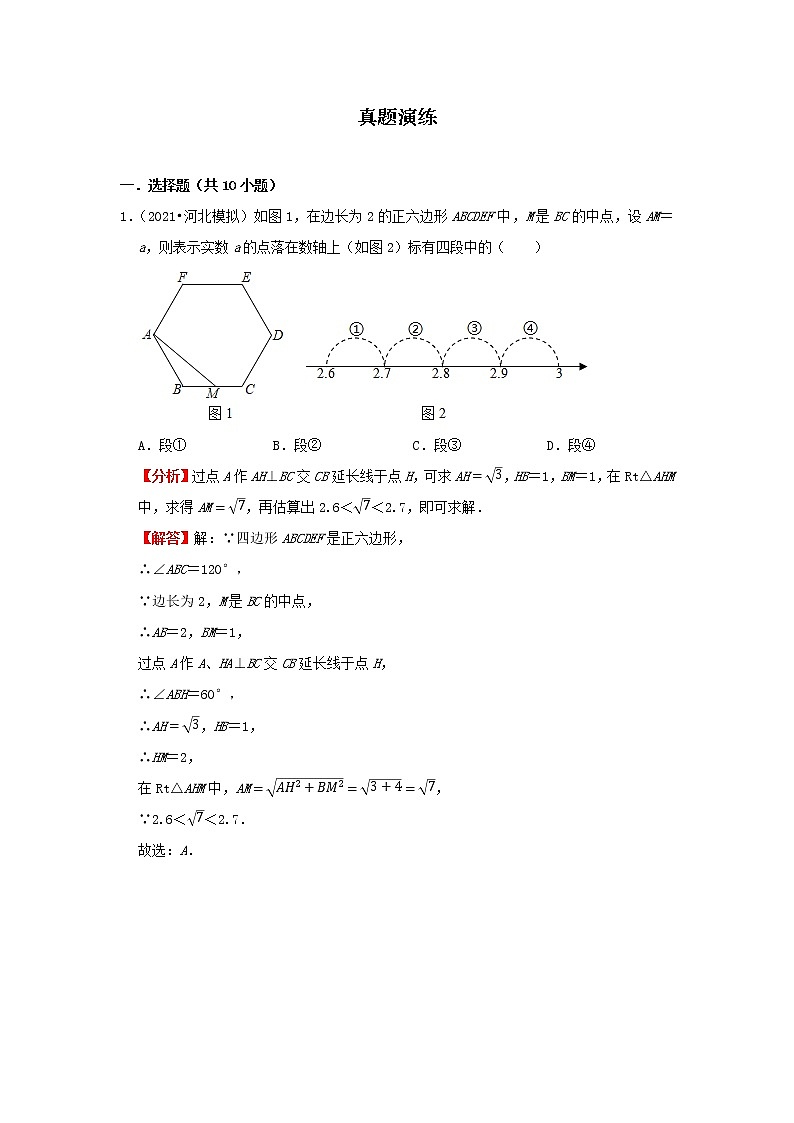
1.(2021•河北模拟)如图1,在边长为2的正六边形ABCDEF中,M是BC的中点,设AM=a,则表示实数a的点落在数轴上(如图2)标有四段中的( )
A.段①B.段②C.段③D.段④
【分析】过点A作AH⊥BC交CB延长线于点H,可求AH=3,HB=1,BM=1,在Rt△AHM中,求得AM=7,再估算出2.6<7<2.7,即可求解.
【解答】解:∵四边形ABCDEF是正六边形,
∴∠ABC=120°,
∵边长为2,M是BC的中点,
∴AB=2,BM=1,
过点A作A、HA⊥BC交CB延长线于点H,
∴∠ABH=60°,
∴AH=3,HB=1,
∴HM=2,
在Rt△AHM中,AM=AH2+BM2=3+4=7,
∵2.6<7<2.7.
故选:A.
2.(2021•唐山一模)已知:如图,正方形面积为8,其边长是x,则关于x的结论中正确的是( )
A.正方形的对角线长是4B.8的平方根是x
C.x是有理数D.x不能在数轴上表示
【分析】根据算术平方根和平方根的意义,无理数的意义,实数与数轴的关系,可得答案.
【解答】解:由题意,得
x=8,
A、对角线长=2x=4,故A符合题意;
B、8的平方根是±8,不等于x,故B不符合题意;
C、x是无理数,故C不符合题意;
D、x可以在数轴上表示,故D不符合题意;
故选:A.
3.(2021•河北模拟)若–▢是正无理数,则▢可以是( )
A.−3B.−227C.0D.3.14
【分析】无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
【解答】解:A、﹣(−3)=3是正无理数,若–▢是正无理数,则▢可以是−3,故此选项符合题意;
B、−227是有理数,故此选项不符合题意;
C、0是有理数,故此选项不符合题意;
D、3.14是有理数,故此选项不符合题意.
故选:A.
4.(2021•路南区三模)如图,数轴上点N所对应的实数为n,则下列实数中所对应的点在数轴上位于﹣1和0之间的是( )
A.1﹣nB.n﹣2C.2﹣nD.n+2
【分析】将点N向右平移2个单位长度即可.
【解答】解:∵﹣3<n<﹣2,
∴﹣1<n+2<0,
故选:D.
5.(2021•迁西县模拟)如图,数轴上点C所表示的数是( )
A.13B.22C.3.6D.3.7
【分析】利用数轴表示数得到OA=3,利用基本作图得到AB=2,再利用勾股定理计算出OB,从而得到OC的长,然后利用数轴表示数的方法得到C点表示的数.
【解答】解:∵OA=3,AB=3﹣1=2,
∴OB=13,
∴OC=OB=13,
∴点C表示的数是13,
故选:A.
6.(2021•河北)若33取1.442,计算33−333−9833的结果是( )
A.﹣100B.﹣144.2C.144.2D.﹣0.01442
【分析】根据实数的运算法则进行计算可得答案.
【解答】解:∵33取1.442,
∴原式=33×(1﹣3﹣98)
≈1.442×(﹣100)
=﹣144.2.
故选:B.
7.(2021•竞秀区一模)以下关于8的说法,错误的是( )
A.8是无理数
B.8=±22
C.2<8<3
D.能够在数轴上找到表示8的点
【分析】根据无理数的定义,算术平方根的定义,无理数的估算,实数与数轴上的点是一一对应关系分别判断即可.
【解答】解:A选项,8=22,所以8是无理数,故该选项正确,不符合题意;
B选项,8=22,一个正数的算术平方根只有一个,故该选项错误,符合题意;
C选项,∵4<8<9,∴2<8<3,故该选项正确,不符合题意;
D选项,边长为2的正方形的对角线=22+22=8,用圆规以O为圆心,8为半径在数轴的正半轴上截取即可,故该选项正确,不符合题意;
故选:B.
8.(2021•裕华区校级模拟)8的值是( )
A.2B.22C.4D.2
【分析】根据算术平方根的定义即可求解.
【解答】解:8的值是22.
故选:B.
9.(2021•定兴县一模)下列四个数:3,﹣0.5,32,−6中,绝对值最大的数是( )
A.3B.﹣0.5C.32D.−6
【分析】根据实数的大小比较解答即可.
【解答】解:下列四个数:3,﹣0.5,32,−6中,绝对值最大的数是3,
故选:A.
10.(2021•石家庄模拟)已知5≤a≤7,4≤b≤6,则a+b的整数部分可以是( )
A.9B.10C.11D.12
【分析】根据估算无理数的大小的方法即可得a+b的整数部分.
【解答】解:∵5≤a≤7,4≤b≤6,
∴25≤a≤49,16≤b≤36,
∴41≤a+b≤85,
则a+b的整数部分可以是6,7,8,9.
故选:A.
二.填空题(共5小题)
11.(2021•河北模拟)若a+2b=2+1,则a2+4ab+4b2= 3 .
【分析】根据完全平方公式、算术平方根、实数的乘方解决此题.
【解答】解:∵a+2b=2+1,
∴(a+2b)2=(2+1)2.
∴a2+4ab+4b2=3.
故答案为:3.
12.(2021•桥东区二模)计算:22−4= 2 .
【分析】直接利用二次根式的性质和有理数的乘方运算法则分别化简,再利用有理数的加减运算法则计算得出答案.
【解答】解:原式=4﹣2
=2.
故答案为:2.
13.(2021•衡水模拟)如果a+2+|b−3|=0,那么ab= ﹣8 .
【分析】根据非负数的性质列式求出a、b的值,然后代入代数式进行计算即可得解.
【解答】解:根据题意得,a+2=0,b﹣3=0,
解得a=﹣2,b=3,
所以,ab=(﹣2)3=﹣8.
故答案为:﹣8.
14.(2021•安次区二模)计算:(15)−1−4= 3 .
【分析】直接利用负整数指数幂的性质以及二次根式的性质分别代入得出答案.
【解答】解:原式=5﹣2
=3.
故答案为:3
15.(2021•长安区二模)已知a=3,则a的值为 9 .
【分析】直接根据算术平方根的定义求解.
【解答】解:∵32=9,
∴9=3,
故答案为:9.
三.解答题(共3小题)
16.(2021•丰润区一模)计算:|−2|+(π+3)0+2cs30°−(13)−1+12.
【分析】由去绝对值、零指数幂、特殊角三角函数、负整数指数幂、平方根运算法则,分别化简、计算即可.
【解答】解:原式=2+1+2×32−3+23
=2+1+3−3+23
=33.
17.(2021•桥西区校级模拟)比较x2+y2与2xy的大小.尝试:用“<”,“=”或“>”填空.
①当x=2,y=2时;x2+y2 = 2xy;
②当x=1,y=3时,x2+y2 > 2xy;
③当x=y=4时,x2+y2 = 2xy;
验证:若x,y取任意实数,x2+y2与2xy有怎样的大小关系?试说明理由;
应用:当xy=1时,请直接写出x2+4y2的最小值.
【分析】①代入求值,再比较即可;
②代入求值,再比较即可;
③代入求值,再比较即可;
验证:将(x﹣y)2≥0变形即可得答案;
应用:利用x2+y2≥2xy可直接得到结果.
【解答】解:①x=2,y=2时,x2+y2=8,2xy=8,
∴x2+y2=2xy,
故答案为:=;
②x=1,y=3时,x2+y2=10,2xy=6,
∴x2+y2>2xy,
故答案为:>;
③x=y=4时,x2+y2=32,2xy=32,
∴x2+y2=2xy,
故答案为:=;
验证:x2+y2≥2xy,理由如下:
∵(x﹣y)2≥0,
∴x2﹣2xy+y2≥0,
∴x2+y2≥2xy;
应用:由验证知:x2+4y2≥2×x•2y
即x2+4y2≥4xy,
∵xy=1,
∴x2+4y2≥4,
∴x2+4y2的最小值是4.
18.(2021•玉田县二模)如图,数轴上有A、B、C三个点,它们所表示的数分别为a、b、c三个数,其中b<0,且b的倒数是它本身,且a、c满足(c﹣4)2+|a+3|=0.
(1)计算:a2﹣2a−c的值;
(2)若将数轴折叠,使得点A与点B重合,求与点C重合的点表示的数.
【分析】(1)利用非负数的性质求出a与c的值,代入原式计算即可求出值;
(2)根据a,b的值,确定出中点坐标,进而求出与C重合的点即可.
【解答】解:(1)∵(c﹣4)2+|a+3|=0,
∴c﹣4=0,a+3=0,
解得:a=﹣3,c=4,
则原式=a2﹣2a−c=(﹣3)2﹣2×(﹣3)−4=9﹣(﹣6)﹣2=13;
(2)∵b<0,且b的倒数是它本身,
∴b=﹣1,
∵a=﹣3,
∴﹣3和﹣1重合,﹣3和﹣1的中点为﹣2,
∵c=4,
∴与点C重合的点表示的数是﹣8;
故答案为:(1)13;(2)﹣8.
相关试卷
这是一份考点02实数运算(解析版)-2022年数学中考一轮复习考点透析(北京版),共11页。试卷主要包含了平方根,算术平方根,立方根,平方根和立方根的性质,比大,比小的整数是,下列命题中,真命题是,下列实数中,在2和3之间的是等内容,欢迎下载使用。
这是一份考点01实数及其运算(解析版)-2022年数学中考一轮复习考点透析(苏科版),共8页。试卷主要包含了1010010001…等;,836×107D.2,1836×108,,9×103B.2,2×103 .,08×106 人.等内容,欢迎下载使用。
这是一份考点01实数的有关概念(解析版)-2022年数学中考一轮复习考点透析(青岛版),共10页。试卷主要包含了 有理数的分类,101001000……,数轴,相反数,倒数,绝对值,科学记数法,近似数等内容,欢迎下载使用。









