

所属成套资源:苏科版2022年数学中考一轮复习考点透析
考点23视图与投影(解析版)-2022年数学中考一轮复习考点透析(苏科版)
展开
这是一份考点23视图与投影(解析版)-2022年数学中考一轮复习考点透析(苏科版),共10页。试卷主要包含了投影,视图等内容,欢迎下载使用。
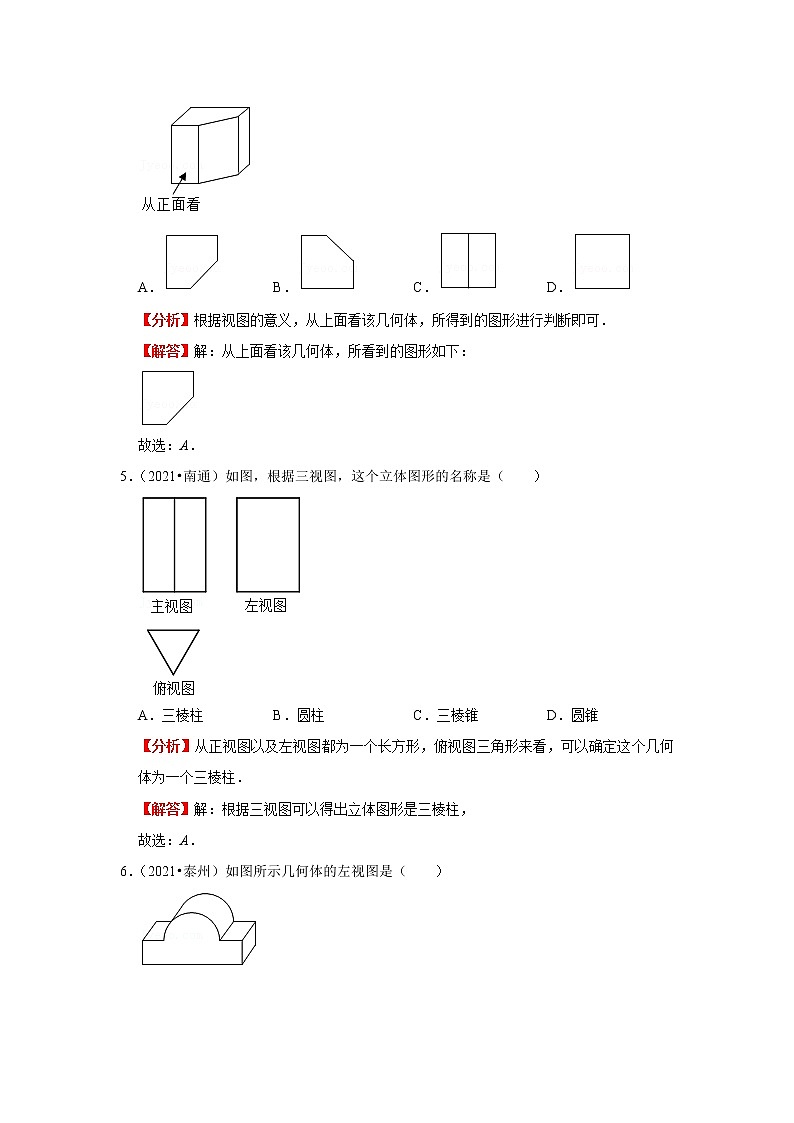
考点23视图与投影考点总结1、投影(1)投影:用光线照射物体,在某个平面上得到的影子叫做物体的投影。(2)平行投影:由平行光线形成的投影是平行投影。(3)中心投影:由同一点发出的光线形成的投影叫做中心投影。(4)正投影:投影线垂直于投影面产生的投影叫做正投影。2、视图(1) 视图:从某一方向观察一个 物体时,所看到的平面图形叫做物体的一个视图。视图可以看作物体在某一方向光线下的正投影。(2)主视图、俯视图、左视图对一个物体在三个 投影面内同时进行正投影,在正面内得到的由前向后观察物体的视图,叫做主视图;在水平面内得到的由上向下观察物体的视图 ,叫 做俯视图;在侧面内得到的由左向右观察物体的视图,叫做左视图。主视图与俯视图的长对正;主视图与左视图的高平齐;左视图与俯视图的宽相等。 真题演练一.选择题(共10小题)1.(2021•东台市模拟)下列四个立体图形中,主视图与其它三个不同的是( )A. B. C. D.【分析】根据图中的主视图解答即可.【解答】解:选项A、B、D的主视图的底层两个小正方形,上层左边一个小正方形,选项C的主视图的底层两个小正方形,上层是两个小正方形,故选:C.2.(2021•西宁)某几何体的三视图如图所示,则此几何体是( )A.圆锥 B.长方体 C.圆柱 D.四棱柱【分析】根据主视图和左视图确定该几何体是柱体还是锥体,然后根据俯视图确定答案即可.【解答】解:∵主视图和左视图均为矩形,∴该几何体为柱体,∵俯视图为圆,∴该几何体为圆柱,故选:C.3.(2021•镇江)如图所示,该几何体的俯视图是( )A.正方形 B.长方形 C.三角形 D.圆【分析】根据俯视图的定义,从上面看该几何体,所得到的图形进行判断即可.【解答】解:从上面看该几何体,所看到的图形是三角形.故选:C.4.(2021•淮安)如图所示的几何体的俯视图是( )A. B. C. D.【分析】根据视图的意义,从上面看该几何体,所得到的图形进行判断即可.【解答】解:从上面看该几何体,所看到的图形如下:故选:A.5.(2021•南通)如图,根据三视图,这个立体图形的名称是( )A.三棱柱 B.圆柱 C.三棱锥 D.圆锥【分析】从正视图以及左视图都为一个长方形,俯视图三角形来看,可以确定这个几何体为一个三棱柱.【解答】解:根据三视图可以得出立体图形是三棱柱,故选:A.6.(2021•泰州)如图所示几何体的左视图是( )A. B. C. D.【分析】根据左视图是从左面看到的图形判定则可.【解答】解:从左边看,是一列两个矩形.故选:C.7.(2021•常州)如图是某几何体的三视图,该几何体是( )A.正方体 B.圆锥 C.圆柱 D.球【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.【解答】解:一个几何体的三视图都是圆,这个几何体是球.故选:D.8.(2021•盐城)如图是由4个小正方形体组合成的几何体,该几何体的主视图是( )A. B. C. D.【分析】根据主视图的意义画出相应的图形,再进行判断即可.【解答】解:该组合体的主视图如下:故选:A.9.(2021•南京)如图,正方形纸板的一条对角线垂直于地面,纸板上方的灯(看作一个点)与这条对角线所确定的平面垂直于纸板.在灯光照射下,正方形纸板在地面上形成的影子的形状可以是( )A. B. C. D.【分析】根据正方形纸板的一条对角线垂直于地面,纸板上方的灯(看作一个点)与这条对角线所确定的平面垂直于纸板,则在地面上的投影关于对角线对称,因为灯在纸板上方,所以上方投影比下方投影要长.【解答】解:根据正方形纸板的一条对角线垂直于地面,纸板上方的灯(看作一个点)与这条对角线所确定的平面垂直于纸板,∴在地面上的投影关于对角线对称,∵灯在纸板上方,∴上方投影比下方投影要长,故选:D.10.(2021•苏州)如图,圆锥的主视图是( )A. B. C. D.【分析】找到从正面看所得到的图形即可.【解答】解:圆锥的主视图是一个等腰三角形,故选:A.二.填空题(共5小题)11.(2021•扬州)如图是某圆柱体果罐,它的主视图是边长为10cm的正方形,该果罐侧面积为 100π cm2.【分析】此几何体为圆柱,那么侧面积=底面周长×高.【解答】解:由题意得圆柱的底面直径为10cm,高为10cm,∴侧面积=10π×10=100π(cm2).故答案为:100π.12.(2021•泰兴市二模)某几何体的三视图如图所示,则这个几何体的表面积为 2108 .【分析】根据三视图得出几何体,进而利用矩形的面积公式解答即可.【解答】解:由图可知,这个几何体有七个面组成,如图所示:这个几何体的表面积为28×15+2×20×16+2(16+10)×8+15×16+15×10+10×15+15×20=420+640+208+240+150+150+300=2108,故答案为:2108.13.(2021•邗江区二模)如图是由6个大小相同的小正方体拼成的几何体,若去掉最左面的小正方体,则视图不发生改变的是 左视图 .(填主视图、左视图或俯视图)【分析】根据从正面看得到的图形是主视图,从左边看得到的图形是左视图,从上边看得到的图形是俯视图,可得答案.【解答】解:若去掉最左面的小正方体,其左视图不变,即左视图依然还是三层,底层两个正方形,第二层有一个,顶层有一个正方形.故答案为:左视图.14.(2021•泰州模拟)小明用彩纸给爸爸做一顶生日帽,其左视图和俯视图如图所示,其中AB=24cm,AC=36cm,则至少需用彩纸 432π cm2(接口处重叠面积不计).【分析】生日帽可看作一个无底面的圆锥体,根据左视图和俯视图,可知底面圆的直径为24cm,母线长36cm,根据圆锥的侧面积公式列式计算即可.【解答】解:由题意可得,所需彩纸至少需要π×12×36=432π(cm2),故答案为:432π.15.(2021•南通模拟)已知几何体三视图如图所示,则这个几何体的侧面积为 20π .【分析】俯视图为圆的只有圆锥,圆柱,球,根据主视图和左视图都是三角形可得到此几何体为圆锥,那么侧面积=底面周长×母线长÷2.【解答】解:此几何体为圆锥;∵直径为8,母线长为,∴侧面积=8π×5÷2=20π.故答案为20π.三.解答题(共2小题)16.(2021•徐州模拟)某公司设计的木制护栏如图2,护栏俯视图的一部分如图1,m是左侧主柱,两侧主柱之间有11根长方体栏杆,栏杆的截面是5cm的正方形(图中a1,a2,…a11),每两根栏杆之间的距离为12.5cm,根据有关标准要求,栏杆间距不得大于11cm,在不增加材料的前提下,能否通过改变安装方案,使栏杆间距符合要求?说明理由.(1.41,1.73,2.24)【分析】由题意得,两主柱之间的距离为12.5×12+11×5=205(cm),将栏杆对角线和护栏平行安装即可.【解答】解:能通过改变安装方案,使栏杆间距符合要求,理由如下:如图,将栏杆对角线和护栏平行安装,两主柱之间的距离为12.5×12+11×5=205cm,栏杆的对角线长是55×1.41=7.05(cm),∴这样安装每两根栏杆之间的距离为10.62(cm)<11cm,∴能通过改变安装方案,使栏杆间距符合要求.17.(2020•邗江区校级一模)双十一购物狂欢节,天猫“某玩具旗舰店”对乐高积木系列玩具将推出买一送一活动.根据积木数量的不同,厂家会订制不同型号的外包装盒.所有外包装盒均为双层上盖的长方体纸箱(上盖纸板面积刚好等于底面面积的2倍,如图1).长方体纸箱的长为a厘米,宽为b厘米,高为c厘米.(1)请用含有a,b,c的代数式表示制作长方体纸箱需要 (2ac+2bc+3ab) 平方厘米纸板;(2)如图2为若干包装好的同一型号玩具堆成几何体的三视图,则组成这个几何体的玩具个数最少为 9 个;(3)由于旗舰店在双十一期间推出买一送一的活动,现要将两个同一型号的乐高积木包装在同一个大长方体的外包装盒内(如图1),已知单个乐高积木的长方体纸盒长和高相等,且宽小于长.如图3所示,现有甲,乙两种摆放方式,请分别计算甲,乙两种摆放方式所需外包装盒的纸板面积(包装盒上盖朝上),并比较哪一种方式所需纸板面积更少,说明理由.【分析】(1)长方体的表面积+上盖的面积,可解答;(2)主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形;(3)分别根据长方体的表面积公式+上盖的面积可得所需纸板面积,并比较大小即可.【解答】解:(1)制作长方体纸箱需要(2ac+2bc+3ab)平方厘米纸板;故答案为:(2ac+2bc+3ab);(2)根据三视图知,则组成这个几何体的玩具个数最少的分布情况如下图所示:所以组成这个几何体的玩具个数最少为9个,故答案为:9;(3)如图3,由题意得:a=c,a>b,甲:2(ac+2bc+2ab)+2ab,乙:2(2ab+2ac+bc)+2ab,∵a>b,∴ac>bc,∴ac﹣bc>0,∵甲所需纸板面积﹣乙所需纸板面积=2(ac+2bc﹣2ac﹣bc)=2(bc﹣ac)<0,∴甲种摆放方式所需外包装盒的纸板面积更少.
相关试卷
这是一份初中数学中考复习 考点33 视图与投影(解析版),共16页。
这是一份考点25投影与视图(解析版)-2022年数学中考一轮复习考点透析(北京版),共14页。试卷主要包含了投影,三视图,解答题等内容,欢迎下载使用。
这是一份考点25统计(解析版)-2022年数学中考一轮复习考点透析(苏科版),共13页。试卷主要包含了调查方式,总体,统计图,平均数,众数,方差与标准差,频数与频率等内容,欢迎下载使用。









