初中数学北师大版八年级下册1 等腰三角形教学ppt课件

这是一份初中数学北师大版八年级下册1 等腰三角形教学ppt课件，文件包含11等腰三角形3教学课件pptx、11等腰三角形3课后练习docx、11等腰三角形3学案设计docx、11等腰三角形3教学设计docx等4份课件配套教学资源，其中PPT共17页， 欢迎下载使用。
1.理解等腰三角形的判定定理，并会运用其进行简单的证明．2.了解反证法的基本证明思路，并能简单应用。
1、等腰三角形都有哪些性质呢？
2、请你把定理“等腰三角形的两个底角相等”的题设与结论反过来说一下.
如果一个三角形有两个角相等，那么这两个角所对的边也相等.
例1：已知：如图，在△ABC中，∠B＝∠C. 求证：AB=AC.
证明：作BC 边上的高 AD. 则∠ADB＝∠ADC＝90 ° ，在△ABD和 △ACD中，∵∠B＝∠C，∠ADB＝∠ADC，AD=AD，∴△ABD ≌△ACD（AAS），∴ AB=AC .
证明：作∠BAC的平分线AD.在△ABD和 △ACD中，∵∠B＝∠C，∠BAD＝∠CAD，AD=AD，∴△ABD≌△ACD（AAS），∴ AB=AC .
想一想：作BC边上的中线行吗?
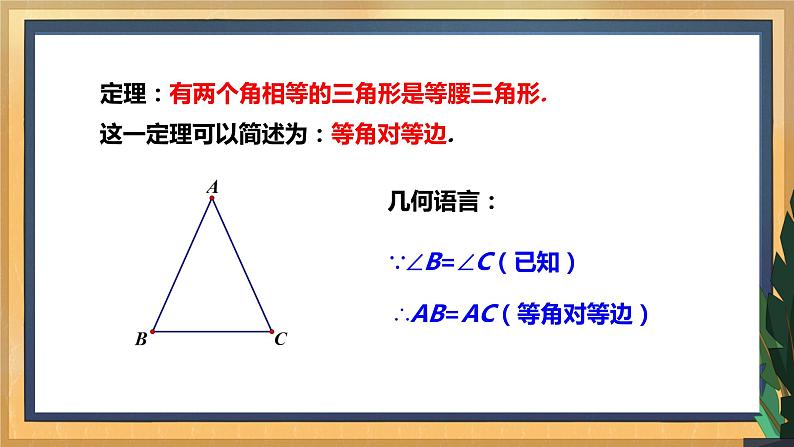
定理：有两个角相等的三角形是等腰三角形.
这一定理可以简述为：等角对等边.
∴AB=AC（等角对等边）
想一想 小明认为，在一个三角形中，如果两个角不相等，那么这两个角所对的边也不相等．你认为小明这个结论成立吗？如果成立，你能证明它吗？
证明：如图，在△ABC中，已知∠B≠∠C，此时AB与AC要么相等，要么不相等．假设AB＝AC，那么根据 “等边对等角”定理可得∠B＝∠C，这与已知条件∠B≠∠C相矛盾，因此AB≠AC．
先假设命题的结论不成立，然后推导出与定义、基本事实、已有定理或已知条件相矛盾的结果从而证明命题的结论一定成立．这种证明方法称为反证法．
（1）假设命题的结论不成立；（2）从这个假设出发，应用正确的推理方法，得出与定义、基本事实、已有定理或已知条件相矛盾的结果;（3）由矛盾的结果判定假设不正确，从而肯定命题的结论正确.
例2 用反证法证明：一个三角形中不能有两个角是直角．已知：△ABC,求证：∠A，∠B，∠C中不能有两个角是直角
证明：假设∠A，∠B，∠C中有两个角是直角，不妨设∠A和∠B是直角，即∠A＝90°，∠B＝90°．于是∠A+∠B+∠C=90°+90°+∠C＞180°．这与三角形内角和定理相矛盾，因此“∠A和∠B是直角”的假设不成立．所以，一个三角形中不能有两个角是直角．
1．下列命题是假命题的是（ ）A．有两个内角是70°与40°的三角形是等腰三角形B．一个外角的平分线平行于一边的三角形是等腰三角形C．有两个内角不相等的三角形不是等腰三角形D．有两个顶点不同的外角相等的三角形是等腰三角形
2．如图，△ABC中，AB=AC，∠A=50°，点D在△ABC内部，且∠DBC=∠DCA，则∠BDC的度数是（ ）A．130° 　　 B．65° 　　 C．120° 　　D．115°3．在等腰三角形中，已知两底角之和等于顶角的2倍，那么这个三角形是（ ）A．直角三角形 　　 　 B．钝角三角形C．等边三角形 　　 　D．是锐角三角形但不是等边三角形
4．在△ABC中，AB=2 cm，∠B=50°，若AC=2 cm，则∠A=_____，∠C=____；如果∠C=50°，则AC=___ _．5．底角等于顶角的一半的等腰三角形是 角形．6．如图，已知：在△ABC中，AB=AC=4 cm，∠ABC=15°，BD⊥AC于点D，则BD=______．
7.求证：如果三角形一个外角的平分线平行于三角形的一边，那么这个三角形是等腰三角形．已知：如图，∠CAE是△ABC的外角，∠1=∠2，AD∥BC求证：AB=AC
证明：∵AD∥BC，∴∠1=∠B，∠2=∠C．∵∠1=∠2，∴∠B=∠C，∴AB=AC．
8.求证：在一个平面内，过直线l外一点P只能作出一条直线垂直于l ．
证明：假设过点P可以作两条直线垂直于直线 如图，那么∠ PAB＝ ∠PBA＝ 90°．于是 ∠P＋∠ PAB＋∠ PBA＞180°． 即△PAB的内角和大于180° ，这与定理“三角形内角和等于180°”相矛盾，故假设不成立．
1．等腰三角形的判定 如果一个三角形有两个角相等，那么这两个角所对的边也相等（简写成“等角对等边”）2．反证法 在证明时，先假设命题的结论不成立，然后推导出与定义、基本事实、已有定理或已知条件相矛盾的结果从而证明命题的结论一定成立．这种证明方法称为反证法．