













北师大版八年级下册2 直角三角形说课课件ppt
展开1、我们学过三角形全等的判定方法有哪几种?
边边边(SSS)、边角边(SAS)、角边角(ASA)、角角边(AAS)
2、两边及其中一边的对角对应相等的两个三角形全等吗?
3、两边相等及其中一边的对角是直角的两个三角形全等吗?
“斜边、直角边”(或“HL”)定理:
如果在两个直角三角形中,已知斜边和一条直角边分别对应相等,那么这两个直角三角形全等吗?
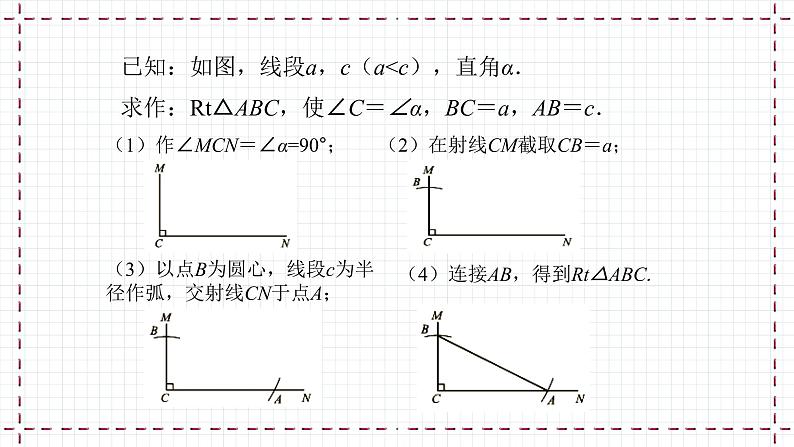
已知一条直角边和斜边,求作一个直角三角形.
已知:如图,线段a,c(a
(1)作∠MCN=∠α=90°;
(2)在射线CM截取CB=a;
(3)以点B为圆心,线段c为半径作弧,交射线CN于点A;
(4)连接AB,得到Rt△ABC.
思考:通过刚才的画图,你有什么发现?
斜边和一条直角边分别对应相等的两个直角三角形全等.
你能证明这个命题是真命题吗?
已知:如图,在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,AB=A′B′,AC=A′C′.
求证:△ABC≌△A′B′C′.
在Rt△ABC中,∵∠C=90°,∴BC2=AB2-AC2(勾股定理).同理,B′C′2=A'B'2-A'C'2(勾股定理).∵AB=A′B′,AC=A′C′,∴BC=B'C'.∴△ABC≌△A′B′C' (SSS)
定理 斜边和一条直角边分别对应相等的两个直角三角形全等
简述为“斜边、直角边”或“HL”
∵在△ABC和△A′B′C′中,∠C=∠C′=90°,
AC=A′C′,AB=A′B′,∴Rt△ABC≌Rt△A′B′C′(HL)
例 如图,有两个长度相等的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠C和∠F的大小有什么关系?
解:根据题意,可知∠BAC=∠EDF=90°,BC=EF,AC=DF,∴Rt△ABC≌Rt△DEF(HL)。∴∠B=∠DEF。∵∠DEF+∠F=90°,∴∠B+∠F=90°。
1.如图,已知∠ACB=∠BDA=90°,要使△ACB≌△BDA,还需要什么条件?把它们分别写出来.
2.已知:如图,D是△ABC的BC边的中点,DE⊥AB,DF⊥AB,垂足分别为E,F,且DE=DF。求证:△ABC是等腰三角形。
这节课大家通过自学和小组合作,相信每个同学都有所收获我掌握的定理: ;我探索的发现: ;我学会的方法: ;我还懂得了: .
1.判断下列命题的真假,并说明理由:(1)两个锐角对应相等的两个直角三角形全等; (2)斜边及一锐角对应相等的两个直角三角形全等; (3)两条直角边对应相等的两个直角三角形全等;
(4)一条直角边和另一条直角边上的中线对应相等的两个直角三角形全等.
2.在△ABC≌△A'B'C'中,CD,C'D'分别是高,并且AC=A'C',CD=C'D'.∠ACB=∠A'C'B'.求证:△ABC≌△A'B'C'.
3.已知:如图,AB=CD,DE⊥AC,BF⊥AC,垂足分别为E,F,且DE=BF.求证:(1)AE=CF;(2)AB∥CD.
说一说直角三角形全等的判定方法?
斜边和一条直角边分别相等的两个直角三角形全等. 简述为“斜边、直角边”或“HL”
必做题:习题1.6 第2题.选做题:习题1.6 第3、5题.
初中数学北师大版八年级下册2 直角三角形完美版备课ppt课件: 这是一份初中数学北师大版八年级下册<a href="/sx/tb_c94876_t3/?tag_id=26" target="_blank">2 直角三角形完美版备课ppt课件</a>,文件包含精选备课北师大版数学八年级下册12直角三角形2课件pptx、精选备课北师大版数学八年级下册12直角三角形2教案doc、精选备课北师大版数学八年级下册12直角三角形2练习doc、精选备课北师大版数学八年级下册12直角三角形2学案doc等4份课件配套教学资源,其中PPT共18页, 欢迎下载使用。
北师大版八年级上册2 一定是直角三角形吗优质课课件ppt: 这是一份北师大版八年级上册2 一定是直角三角形吗优质课课件ppt,文件包含12一定是直角三角形吗pptx、第一章勾股定理12一定是直角三角形吗教学详案docx、12一定是直角三角形吗学案+练习docx等3份课件配套教学资源,其中PPT共25页, 欢迎下载使用。
初中数学北师大版七年级上册1.2 展开与折叠获奖ppt课件: 这是一份初中数学北师大版七年级上册1.2 展开与折叠获奖ppt课件,文件包含2展开与折叠第2课时pptx、2展开与折叠第2课时doc等2份课件配套教学资源,其中PPT共11页, 欢迎下载使用。













