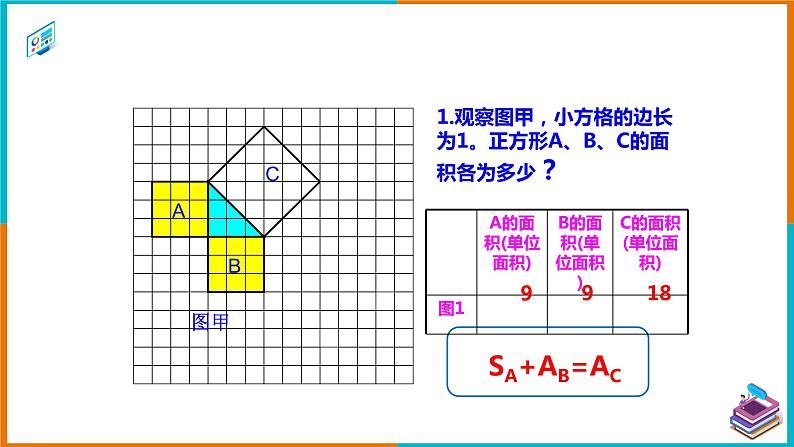
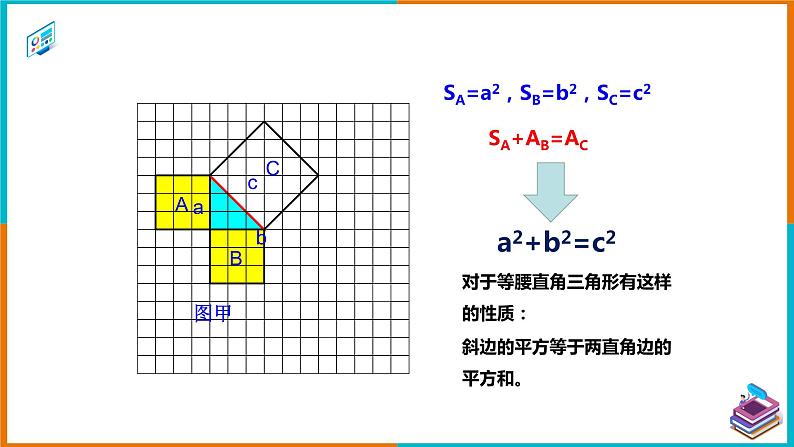
2021学年17.1 勾股定理练习题ppt课件

17.1.1 勾股定理 练习

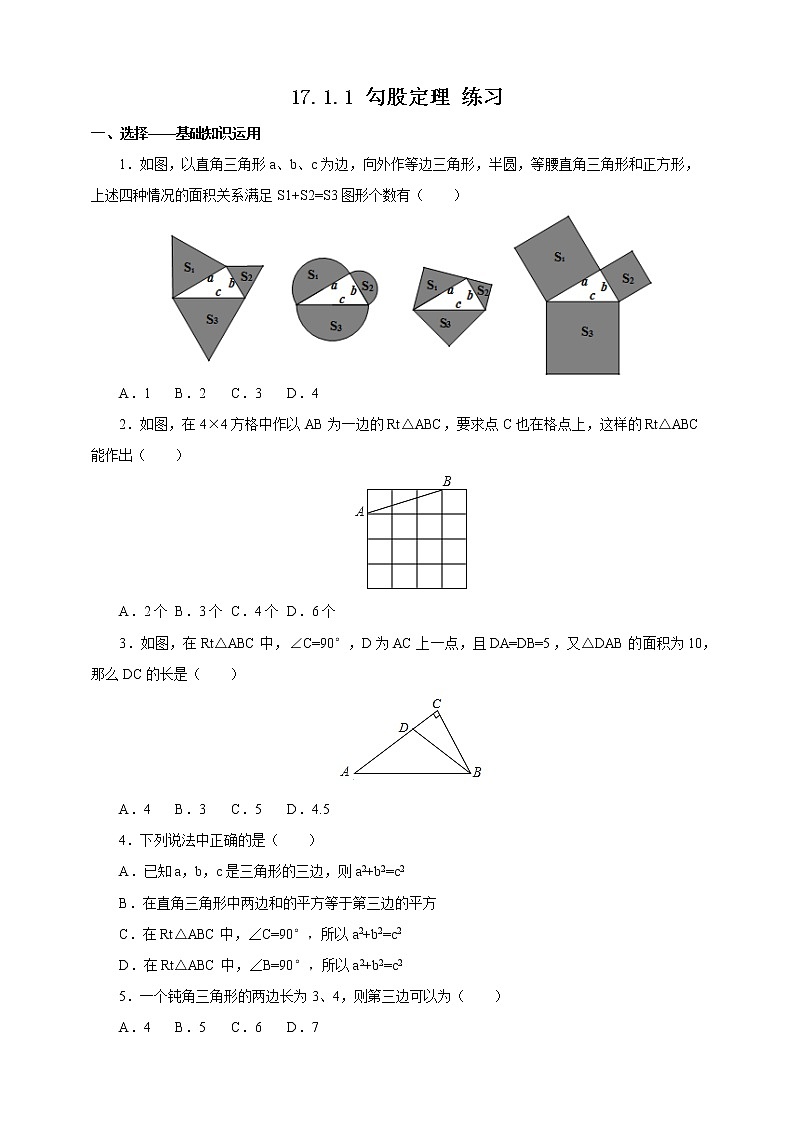
一、选择——基础知识运用

1．如图，以直角三角形a、b、c为边，向外作等边三角形，半圆，等腰直角三角形和正方形，上述四种情况的面积关系满足S1+S2=S3图形个数有（　　）

A．1 B．2 C．3 D．4

2．如图，在4×4方格中作以AB为一边的Rt△ABC，要求点C也在格点上，这样的Rt△ABC能作出（　　）

A．2个 B．3个 C．4个 D．6个

3．如图，在Rt△ABC中，∠C=90°，D为AC上一点，且DA=DB=5，又△DAB的面积为10，那么DC的长是（　　）

A．4 B．3 C．5 D．4.5

4．下列说法中正确的是（　　）

A．已知a，b，c是三角形的三边，则a2+b2=c2

B．在直角三角形中两边和的平方等于第三边的平方

C．在Rt△ABC中，∠C=90°，所以a2+b2=c2

D．在Rt△ABC中，∠B=90°，所以a2+b2=c2

5．一个钝角三角形的两边长为3、4，则第三边可以为（　　）

A．4 B．5 C．6 D．7

6．如图所示，三个正方形中两个的面积分别为S1=169，S2=144，则S3=（　　）

A．50    B．25    C．100    D．30

二、解答——知识提高运用

7．在四边形ABCD中（见图），线段BC长5，∠ABC为直角，∠BCD为135°，AC=AD，而且点A到边CD的垂线段AE的长为12，线段ED的长为5，求四边形ABCD的面积。

8．画一个直角三角形，分别以它的三条边为边向外作等边三角形，要求：

（1）画出图形；

（2）探究这三个等边三角形面积之间的关系，并说明理由。

9．已知△ABC是边长为2的等边三角形，△ACD是一个含有30°角的直角三角形，现将△ABC和△ACD拼成一个凸四边形ABCD．

（1）画出四边形ABCD；

（2）求出四边形ABCD的对角线BD的长。

10．如图所示．从锐角三角形ABC的顶点B向对边作垂线BE．其中AE=3√3，AB=5√3，∠EBC=30°，求BC。

11．设计师要用四条线段CA，AB，BD，DC首尾相接组成如图所示的两个直角三角形图案，∠C与∠D为直角，已知其中三条线段的长度分别为1cm，9cm，5cm，第四条长为xcm，试求出所有符合条件的x的值。

参考答案

一、选择——基础知识运用

1．【答案】D

【解析】（1）S1=a2，S2=b2，S3=c2，

∵a2+b2=c2，

∴a2+b2=c2，

∴S1+S2=S3．

（2）S1=a2，S2=b2，S3=c2，

∵a2+b2=c2，

∴a2+b2=c2，

∴S1+S2=S3．

（3）S1=a2，S2=b2，S3=c2，

∵a2+b2=c2，

∴a2+b2=c2，

∴S1+S2=S3．

（4）S1=a2，S2=b2，S3=c2，

∵a2+b2=c2，

∴S1+S2=S3．

综上，可得

面积关系满足S1+S2=S3图形有4个。

故选：D。

2．【答案】D

【解析】

当AB是斜边时，则第三个顶点所在的位置有：C、D，E，H四个；

当AB是直角边，A是直角顶点时，第三个顶点是F点；

当AB是直角边，B是直角顶点时，第三个顶点是G。

因而共有6个满足条件的顶点。

故选D。

3．【答案】B

【解析】∵在Rt△ABC中，∠C=90°，

∴BC⊥AC，即BC是△DAB的高，

∵△DAB的面积为10，DA=5，

∴DA•BC=10，

∴BC=4，

∴CD===3。

故选B。

4．【答案】C

【解析】在直角三角形中只有斜边的平方等于其他两边的平方的和，且斜边对角为直角。

A、不确定c是斜边，故本命题错误，即A选项错误；

B、不确定第三边是否是斜边，故本命题错误，即B选项错误；

C、∠C=90°，所以其对边为斜边，故本命题正确，即C选项正确；

D、∠B=90°，所以斜边为b，所以a2+c2=b2，故本命题错误，即D选项错误；

故选 C。

5．【答案】C

【解析】设第三边为c，

若这个三角形为直角三角形，则第三边为=5，

∵钝角大于直角，

∴c＞5，

∵三角形第三边小于其余两边和，

∴c＜7，

故选C。

6．【答案】C

【解析】根据图形及勾股定理得：S1=S2+S3，

∵S1=169，S2=144，

∴S3=S1-S2=169-144=25．

故选C。

二、解答——知识提高运用

7．【答案】90

【解析】

∵AC=AD，且AE⊥CD，∴E为CD的中点，

即CE=DE=5，∴△ACD的面积S=•CD•AE=60，

且AC==13，

∴在直角△ABC中，AB==12，

∴△ABC的面积S=•BC•AB=30，

故四边形ABCD的面积为30+60=90。

答：四边形ABCD的面积为 90。

8．【答案】（1）如图1所示；

（2）如图2所示：

斜边所在等边三角形的面积是另外两个等边三角形面积之和，

即S1+S2=S3，

理由如下：

∵△ABC是直角三角形，

∴AB2+AC2=BC2，

∵S3=BC2，S1=AB2，S2=AC2，

∴S1+S2=（AB2+AC2）=AB2=S3。

9．【答案】（1）四边形ABCD分为2种情况，①AC为斜边；②AC为60°角所对直角边；③AC为30°角所对直角边．

所以，共6种图形．

（2）如图，分别求BD的长度，

在图1中，BD===；

在图2中，BD=== ；

在图3中，BD===；

在图4中，BD===；．

在图5中，BD==2；

在图6中，BD==2

答：BD的长度为；2；。

10．【答案】在直角△AEB中，AE=3，AB=5，

则BE==4，

∵∠BEC=90°，∠EBC=30°，

∴BC=2CE（直角三角形中30°角所对直角边为斜边长的一半），

∵BC2=CE2+BE2，

∴3CE2=BE2=48，

∴CE=4，BC=8．

答：BC的长为 8．。

11．【答案】显然AB是四条线段中最长的线段，分AB=x或AB=9两种情况来讨论。

把AB平移至ED（如图所示）。

①若AB=x，

当CD=9时，则x==3；

当CD=5时，则x==5；

当CD=1时，则x==．

②若AB=9，

当CD=5时，由（x+1）2+52=92，得x=2-1；

当CD=1时，由（x+5）2+12=92，得x=4-5；

当CD=x时，由x2+（1+5）2=92，得x=3。