2021学年18.1.1 平行四边形的性质多媒体教学ppt课件

这是一份2021学年18.1.1 平行四边形的性质多媒体教学ppt课件，文件包含1811平行四边形的性质课件pptx、1811平行四边形的性质教案doc、1811平行四边形的性质练习doc、1811平行四边形的性质学案doc等4份课件配套教学资源，其中PPT共44页， 欢迎下载使用。
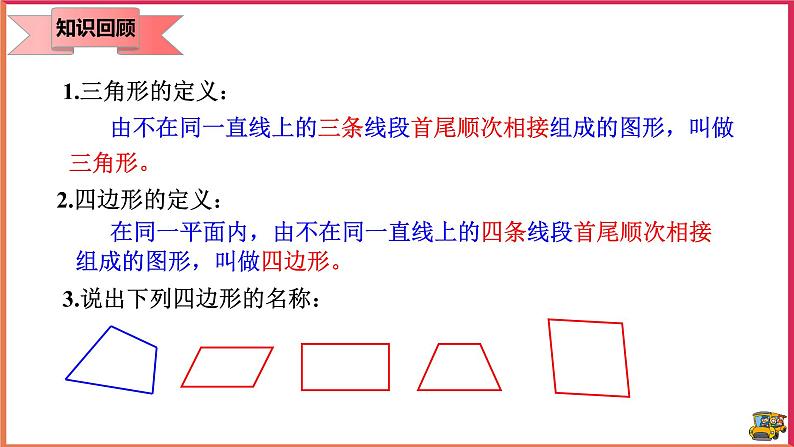
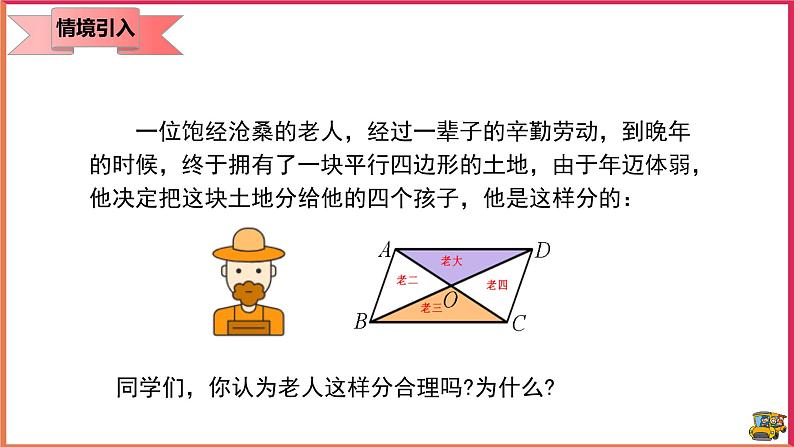
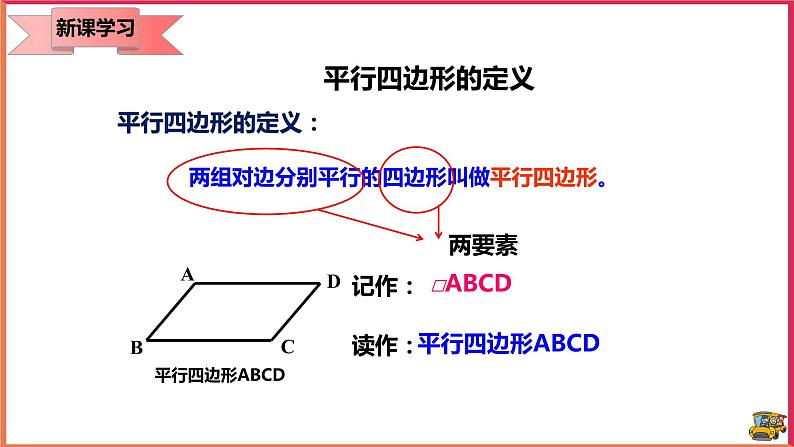
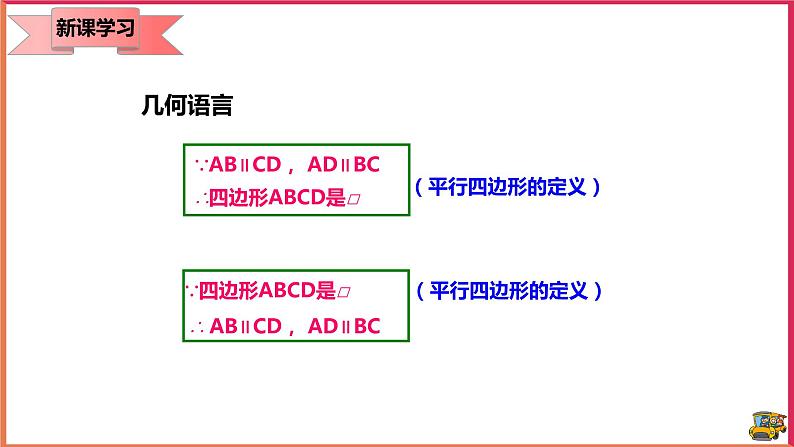
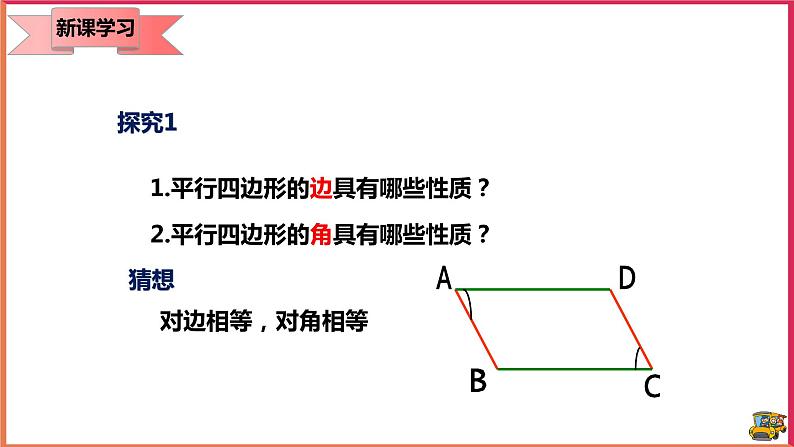
18.1.1 平行四边形的性质 教案【教学目标】1.知识与技能（1）记住平行四边形的相关概念，探究平行四边形的性质。（2）会添加辅助线证明性质，记住性质并能应用性质解决简单的计算。2.过程与方法进一步发展合情推理、演绎推理的能力，增强几何直观和几何符号意识。3.情感态度和价值观培养学生独立思考的习惯与合作交流的意识，激发学生探索数学的兴趣，体验探索成功后的快乐。【教学重点】1、探索并证明平行四边形的性质。2、应用平行四边形的性质进行简单计算、推理。【教学难点】正确利用平行四边形的性质解决问题【教学过程】一、知识回顾    1.三角形的定义：由不在同一直线上的三条线段首尾顺次相接组成的图形，叫做三角形。2.四边形的定义：    在同一平面内，由不在同一直线上的四条线段首尾顺次相接组成的图形，叫做四边形。3.说出下列四边形的名称：       二、情景导入    一位饱经沧桑的老人，经过一辈子的辛勤劳动，到晚年的时候，终于拥有了一块平行四边形的土地，由于年迈体弱，他决定把这块土地分给他的四个孩子，他是这样分的：  同学们，你认为老人这样分合理吗?为什么?三、新课教学寻找生活中的平行四边形  1．平行四边形的定义要了解平行四边形的的性质，我们就要先了解什么是平行四边形，从图形中，我们很容易总结出平行四边形的定义：有两组对边分别平行的四边形叫做平行四边形。对于一个如图所示的平行四边形，我们一般用符号□表示，如平行四边形ABCD记作：□ABCD，读作：平行四边形ABCD。对于平行四边形的定义，我们用几何语言表示：∵AB∥CD   AD∥BC∴四边形ABCD是平行四边形（平行四边形的定义）。反过来∵四边形ABCD是平行四边形（或在□ABCD中）∴AB∥CD   AD∥BC（平行四边形的定义）。2、平行四边形的性质1从定义中，我们能够看到，平行四边形的两组对边分别平行，那么它的对角有什么关系呢？对边又有其他的关系吗？猜想：对角相等，对边相等大家可以动手，按照平行四边形的定义，画出一个平行四边形，然后，用直尺量一下对边的长度，用量角器量一下对角的度数。大家能够发现什么规律吗？AB=DC，AD=BC，∠A=∠C，∠B=∠D由此，我们发现，我们的猜想是正确的，那么大家能够用自己所学的知识来证明一下这个结论吗？在证明之前，我想先让大家考虑这样一个问题，用两个全等的三角形纸片可以拼出几种形状不同的平行四边形？大家可以动手试一下。（学生动手）大家都拼的很好，从中大家有什么启示呢？平行四边形可以是由两个全等的三角形组成，因此在解决平行四边形的问题时，通常可以连结对角线转化为两个全等的三角形进行解题。由刚刚得到的结论，我们就来考虑一下如何证明平行四边形的性质吧。课件展示证明过程。了解了对边与对角的性质之后，大家来思考这样一个问题，已知平行四边形一个内角的度数，你能确定其他内角的度数吗？展示一个平行四边形，由学生回答。刚刚大家都很迅速的得出了结论，大家有什么简单的方法吗？（学生回答）这就是简单的利用了平行四边形的对角相等的性质，∠A+∠B=180°，由此来计算其他三个角的度数。平行四边形中知道一个角就可以求出另外三个角的度数。例1的讲解。学习了平行四边形之后，我们来看另外一个问题，若a // b，作 DA // HG ，分别交 b于D、H，交 a于A、G。则线段DA与HG有什么关系？（学生回答）由平行四边形的对边相等可知，DA=HG，同样的，再画一条平行线之后，得到同样的结论。由此，我们知道，两条平行线之间的平行线段相等。若a // b，DA、GH、CB垂直于 a，交a于A、G、B，交 b于D、H、C。则线段同样相等。在这里，我们看到，是点到直线的距离。由此，我们介绍这样的概念：两条平行线中，一条直线上任意一点到另一条直线的距离，叫做这两条平行线之间的距离。两条平行线之间的距离相等。【练习】1、已知一点到两条平行线的距离分别是1cm，4cm，则这两条平行线之间距离是         3或5      cm。3、平行四边形性质2研究了平行四边形的对边与对角的关系之后，我们再来看它的另外一个——对角线的性质。探究：如图，在□ ABCD中，连接AC，BD，并设它们相交于点O。OA与OC，OB与OD有什么关系？大家来看这个图形，把两张完全相同的平行四边形纸片叠合在一起,在它们的中心O 钉一个图钉，将一个平行四边形绕O旋转180°，你发现了什么？课件展示。从刚刚的实验中，我们发现，旋转之后，两个图形是完全重合的，也就是说我们的猜想是正确的。你能证明这个猜想吗？课件展示证明过程。由此，我们得到平行四边形的性质定理2：平行四边形的对角线互相平分。【典题精讲】1、如图，平行四边形ABCD中，AC=AB，求证：∠ABD=∠DAC。解：∵四边形ABCD是平行四边形，∴AC=2AO，AD∥BC，∵AC=AB，∴AO= AB，∴ =，∵ = = ，∴＝ ，∵∠CAB=∠CAB，∴△AOB∽△ABC，∴∠ABD=∠ACB，∵AD∥BC，∴∠ACB=∠DAC，∴∠ABD=∠DAC2、如图，在▱ABCD中，AE是∠BAD的平分线交DC于点E，求证：CE+BC=AB。解：∵四边形ABCD是平行四边形，∴AD=BC，AB=CD，AB∥CD，∴∠DEA=∠EAB，∵AE是∠BAD的平分线，∴∠DAE=∠EAB，∴∠DAE=∠DEA，∴DE=AD，∴DC=AD+CE，∴AB=CE+BC，即CE+BC=AB．【知识巩固】1、在平行四边形ABCD中，∠A+∠C=140°，那么∠A=   70°  ，∠D=    110°  。2、如图，在□ABCD中，E，F分别是DC，BA延长线上的点，且AE∥CF，AE，CF分别交BC，AD于点G，H，求证：EG=FH。解：∵四边形ABCD是平行四边形，∴AB∥CD，AD∥BC，∵AE∥CF，∴四边形AECF与四边形AGCH是平行四边形，∴AE=CF，AG=CH，∴AG-AE=CH-CF，∴EG=FH3、平行四边形的两邻边的比是2：5，周长为28cm，求平行四边形的各边的长．解：根据平行四边形的性质可知：邻边之和为周长的一半，设较短的边为2x，则较长的为5x，∴2x+5x=14，∴x=2，∴5x=5×2=10，2x=2×2=4，∴平行四边形的各边的长分别为10cm、4cm、10cm、4cm．4、如图，在□ABCD中，对角线AC与BD相交于点O，BD=2AB，E是OA的中点．求证：BE⊥AC。解：∵四边形ABCD是平行四边形，∴BD=2OB，∵BD=2AB，∴OB=AB，又∵E为OA的中点，∴BE⊥AC．    5、如图，平行四边形ABCD中，AC=AB，求证：∠ABD=∠DAC。解：∵四边形ABCD是平行四边形，∴AC=2AO，AD∥BC，∵AC=AB，∴AO= AB，∴ =，∵ = = ，∴＝ ，∵∠CAB=∠CAB，∴△AOB∽△ABC，∴∠ABD=∠ACB，∵AD∥BC，∴∠ACB=∠DAC，∴∠ABD=∠DAC 【达标检测】1、如图，在□ABCD中，CE⊥AB，E为垂足，如果∠BCE=35°，则∠D的度数为（　A　）A．55° B．35° C．25° D．30°2、在平行四边形ABCD中，∠A：∠B：∠C：∠D的值可能是（　D　）A．1：2：3：4         B．1：2：2：1 C．2：2：1：1         D．2：1：2：13、如图，平行四边形ABCD中，AB=6，BC=8，AC的垂直平分线交AD于E，则三角形CDE的周长是（　C　）A．6 B．8 C．14 D．16．4、如图，在□ABCD中，AE是∠BAD的平分线交DC于点E，求证：CE+BC=AB。解：∵四边形ABCD是平行四边形，∴AD=BC，AB=CD，AB∥CD，∴∠DEA=∠EAB，∵AE是∠BAD的平分线，∴∠DAE=∠EAB，∴∠DAE=∠DEA，∴DE=AD，∴DC=AD+CE，∴AB=CE+BC，即CE+BC=AB。【拓展提升】1、已知如图，E、F为□ABCD的对角线AC所在直线上的两点，AE=CF，求证：BE=DF．（用两种方法证明）解：方法①：∵四边形ABCD是平行四边形，∴AB∥DC，AB=DC。∴∠BAC=∠DCA。∴∠BAE=∠DCF，在△ABE和△CDF中，AE＝CF  ；∠BAE＝∠DCF；AB＝CD ，∴△ABE≌△CDF（SAS），∴BE=DF。方法②：连接DE、BF，连接BD交AC于O，如图所示：∵四边形ABCD是平行四边形，∴OA=OC，OB=OD，∵AE=CF，∴OE=OF，∴四边形BFDE是平行四边形，∴BE=DF。2、求证：平行四边形两条对角线的平方和等于四条边的平方和。证明：作AE⊥BC于点E，DF⊥BC交BC的延长线于F，则∠AEB=∠DFC=90°．∵四边形ABCD是平行四边形，∴AB=DC，AB∥CD，∴∠ABE=∠DCF，∴△ABE≌△DCF，∴AE=DF，BE=CF．在Rt△ACE和Rt△BDF中，由勾股定理，得AC2=AE2+EC2=AE2+（BC-BE）2，BD2=DF2+BF2=DF2+（BC+CF）2=AE2+（BC+BE）2，∴AC2+BD2=2AE2+2BC2+2BE2=2（AE2+BE2）+2BC2．又∵AE2+BE2=AB2，即：AC2+BD2=2（AB2+BC2）．∵AB=CD，AD=BC，∴AC2+BD2=AB2+BC2+CD2+AD2【课堂总结】1、平行四边形的定义：两组对边分别平行的四边形叫做平行四边形。2、平行四边形的性质：平行四边形的对边相等。平行四边形的对角相等。平行四边形的对角线互相平分。【教学反思】平行四边形的性质是本节课的重点，而探究性质更是本节课的难点，所以在这个环节里我需要把难点击破，那就需要学生进行配合，教学相长。实践出真知！我通过小组合作的方式让学生自己动手操作，结合“想一想、量一量、拼一拼”等过程，尤其是对两个全等三角形进行拼凑成平行四边形，使他们实际操作中验证性质的成立并能从中体会性质的证明思路。通过小组间的合作交流学习，进行有的放矢的探究活动，把平行四边形转化为我们熟知的三角形，由已知探未知，从中形成科学的“猜想——验证——实验”的解题思路，养成科学的学习习惯。这是从感性认识到理性认识的一个飞跃过程。