2020-2021学年2.1.1同底数幂的乘法授课ppt课件

这是一份2020-2021学年2.1.1同底数幂的乘法授课ppt课件，文件包含211同底数幂的乘法课件pptx、211同底数幂的乘法教案doc、211同底数幂的乘法学案doc、211同底数幂的乘法练习doc等4份课件配套教学资源，其中PPT共18页， 欢迎下载使用。

2³读作什么？表示什么意义？(-5)²呢？你会计算吗？
2³读作2的3次幂，表示3个2相乘，即2×2×2. (-5)²读作-5的2次幂，表示2个-5相乘，即(-5)×(-5).
2³=2×2×2=8， (-5)²=(-5)×(-5)=25.
2³读作什么？表示什么意义？(-5)² ？你会计算吗？
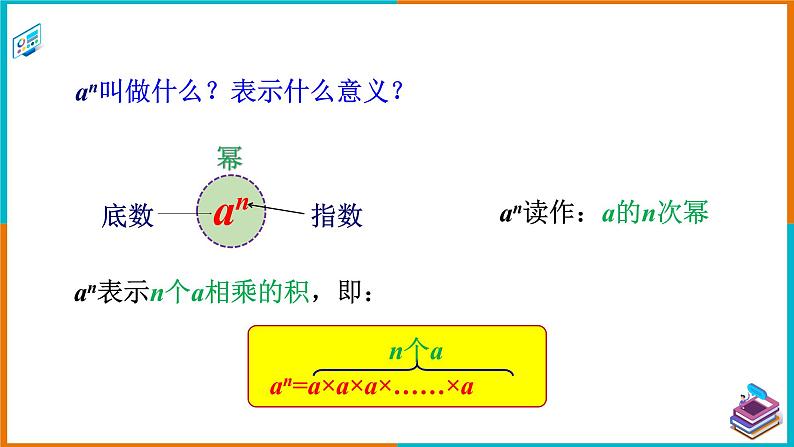
an叫做什么？表示什么意义？
an表示n个a相乘的积，即：
问题一：1.25代表什么？ 2.10×10 ×10 ×10 ×10可以写成什么形式？
25=_________________( 乘方的意义)10×10 ×10 ×10 ×10=______( 乘方的意义)
2×2 ×2 ×2 ×2
问题二：1.式子103×102的意义是什么？ 2.这个式子中的两个因式有何特点？
1.103与102的积2.底数相同
问题：一种电子计算机每秒可进行1014次运算，它工作103秒可进行多少次运算？
=（10×···× 10 ）×（ 10×10×10 ）
=（10×10×···×10）
25×22 = (2 × 2 ×2×2× 2) ×(2 × 2) =________________________=2( ) ；
合作探究：请你根据乘方的意义理解，完成下列填空.
(2)a3×a2 = (a×a×a ) ×(a×a ) =_________________= a( ) ；
(3) 5m · 5n =(5×···×5) ×(5×···×5) = 5( ).
2×2 ×2 × 2×2×2×2
思考：观察上面各题左右两边，底数、指数有什么关系？
22×24= ； a2·a4= ；a2·am= ；（m是正整数）
通过观察，你发现上述式子的指数和底数是怎样变化的？
我们把上述运算过程推广到一般情况（即am·an），即
am·an=am+n（m，n都是正整数）.
同底数幂相乘,底数不变,指数相加 即 am · an = am+n (m、n都是正整数)
条件：①乘法 ②底数相同结果：①底数不变 ②指数相加
总结：同底数幂的乘法法则：
计算：（1） 105×103； （2） x3·x4.
上面两题是 ，可利用 的乘法法则计算。
解：（1） 105×103=105+3=108.
（2） x3·x4=x3+4=x7.
计算：（1） ﹣a·a3； （2） yn·yn+1.
第⑴题负号后面a·a3是底数为a的幂相乘，注意“a”的指数为1；第⑵题指数中含有字母，结果需合并同类项。
解：（1） ﹣a·a3=﹣a1+3=﹣a4.
（2） yn·yn+1=yn+n+1=y2n+1.
下面两题能利用同底数幂的乘法法则计算吗? 如果能，怎样算？
（1） (-a)3·a2； （2） (a-b)2·(b-a)4.
不能直接利用，但变形后能用同底数幂的乘法法则计算.
解：（1） (-a)3·a2=-a3·a2=-a3+2=-a5；
（2） (a-b)2·(b-a)4=(a-b)2·(a-b)4=(a-b)2+4=(a-b)6.
温馨提示：
同底数幂相乘时，指数是相加的；底数为负数时，先用同底数幂的乘法法则计算，最后确定结果的正负；不能忽视指数为1的情况；公式中的a可为一个有理数、单项式或多项式（整体思想）
思考：当三个或三个以上的同底数幂相乘时，怎样用公式表示运算的结果呢？
am· an· ap = am+n+p （m、n、p都是正整数)
（当m、n、p都是正整数时) am· an· ap =？
【例3】计算：（1）32×33×34； （2）y·y2·y4.
解法一：（1）32×33×34=（32×33）×34=35×34=39； （2）y·y2·y4=（y·y2）·y4=y3·y4=y7.
解法二：（1）32×33×34=32+3+4=39； （2）y·y2·y4=y1+2+4=y7.