初中数学第五章 相交线与平行线综合与测试同步训练题

第五章 《相交线与平行线》单元测试卷

（时间80分钟，共100分）           

一、选择题(每题3分，共30分)

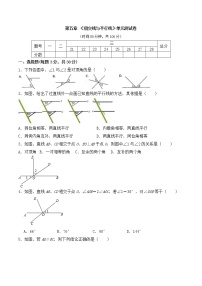
1. 如图，∠1与∠2是同位角的是 (      )

A.①③ B.②③ C.③④ D.②④

2. 如图,直线AB,CD相交于点O,作射线OE,则图中邻补角有 (　　)

A.4对 B.6对 C.7对 D.8对

3. 如图，，，，则的度数是（    ）

A．         B．    C．         D．

4．如图，直线AB、CD相交于点O，∠AOE＝2∠AOC，若∠1＝38°，则∠DOE等于（　　）

A．66° B．76° C．90° D．144°

5．如图，若AD∥BC，则下列结论正确的是（　　）

A．∠1＝∠3 B．∠2＝∠4 C．∠1＝∠2 D．∠2＝∠3

6．一学员练习驾驶汽车，两次拐弯后，行驶的方向与原来的方向相同，这两次拐弯的角度可能是

A. 第一次向左拐，第二次向右拐

B. 第一次向右拐，第二次向左拐

C. 第一次向右拐，第二次向右拐

D. 第一次向左拐，第二次向左拐

7．如图，，点在上，，，则下列结论正确的个数是（    ）

（1）；（2）；（3）；（4）

A．1个 B．2个 C．3个 D．4个

8．将一副三角板按如图放置，如果，则有是（    ）

A．15° B．30° C．45° D．60°

10.如图，，CB平分，BD平分，且，下列结论：平分；；；，其中结论正确的个数有

A. 1个 B. 2个 C. 3个 D. 4个

二、填空题(每题3分，共24分)

11．如图所示,若∠AEC=100°,则当∠D=　　　　°时,AB∥DF. 

12．如图,∠1=70°,直线a向右平移后得到直线b,则∠2-∠3=　　　　°. 

13．把“同角的补角相等”改为如果…，那么…的形式：　   　．

14．已知线段AB的长度为3厘米，现将线段AB向左平移4厘米得到线段CD，那么线段CD的长度为　   　厘米．

15．如图，计划把河水引到水池A中，可以先引AB⊥CD，垂足为B，然后沿AB开渠，则能使所开的渠最短，这样设计的依据是　   　．

16．如图，直线a，b与直线c相交，给出下列条件：①∠1＝∠2；②∠3＝∠6；③∠4+∠7＝180°；④∠5+∠3＝180°，其中能判断a∥b的是　   　（填序号）．

17．如图，AB与DE相交于点O，OC⊥AB，OF是∠AOE的角平分线，若∠COD＝36°，则∠AOF＝　   　．

18．如图，DE∥BC，EF∥AB，图中与∠BFE互补的角有　   　个．

三.解答题(共46分)

19．（6分）如图，和分别在同一直线上，分别交于点．已知．求证：．

20. （8分）如下图所示．求证：

21. （8分）已知如右图所示，，求证

22.（8分）如图，已知∠1+∠2＝180°，∠3＝∠B．

（1）试判断DE与BC的位置关系，并说明理由．

（2）若DE平分∠ADC，∠2＝3∠B，求∠1的度数．

23．（8分）图1，点E在直线AB上，点F在直线CD上，EG⊥FG．

(1)若∠BEG＋∠DFG＝90°，请判断AB与CD的位置关系，并说明理由；

(2)如图2，在(1)的结论下，当EG⊥FG保持不变，EG上有一点M，使∠MFG＝2∠DFG，则∠BEG与∠MFG存在怎样的数量关系？并说明理由；

(3)如图2，若移动点M，使∠MFG＝n∠DFG，请直接写出∠BEG与∠MFG的数量关系．

24．（8分）学校准备在升旗台的台阶上铺设一种红色的地毯（含台阶最上层），已知这种地毯的批发价为每平方米40元，升旗台的台阶宽为3米，其侧面如图所示，请你测算一下，买地毯至少需要多少元？

参考答案

一、选择题:

二、填空题:

11．80

13．解：“同角的补角相等”改为如果…，那么…的形式：如果两个角都是同一个角的补角，那么这两个角相等．

故答案为如果两个角都是同一个角的补角，那么这两个角相等．

14．解：经过平移，对应点所连的线段平行且相等，对应线段平行且相等．将线段AB向左平移4厘米得到线段CD，

则AB＝CD＝3厘米．

故答案为：3．

15．解：这样设计的依据是根据垂线段最短，

故答案为：垂线段最短．

16．解：①∵∠1＝∠2，

∴a∥b，故此选项正确；

②∠3＝∠6无法得出a∥b，故此选项错误；

③∵∠4+∠7＝180°，

∴a∥b，故此选项正确；

④∵∠5+∠3＝180°，

∴∠2+∠5＝180°，

∴a∥b，故此选项正确；

故答案为：①③④．

17．解：∵OC⊥AB，

∴∠AOC＝90°．

∵∠COD+∠AOC+∠AOE＝180°，∠COD＝36°，

∴∠AOE＝54°．

又∵OF是∠AOE的角平分线，

∴∠AOF＝∠AOE＝27°．

故答案为：27°．

18．解：∵DE∥BC，

∴∠DEF＝∠EFC，∠ADE＝∠B，

又∵EF∥AB，

∴∠B＝∠EFC，

∴∠DEF＝∠EFC＝∠ADE＝∠B，

∵∠BFE的邻补角是∠EFC，

∴与∠BFE互补的角有：∠DEF、∠EFC、∠ADE、∠B．

故答案为：4．

三.解答题:

19．【答案】

∵，

∴

∴

∴

又∵

∴

∴

∴

20 【答案】

把，，都集中在某一顶点处，证明它们可构成一周角，或把它们其中某一个角分成两部分，证明每一部分分别与另两角的和是．

证法1：

如图，过点作，交于，

因为，所以

因为，

所以

所以

因为

所以

证法2：

如图，过点作，则

因为，所以，

所以

又，∴

即

证法3：

如图，延长交延长线于．

因为，

所以，为的外角

所以

因为为是的补角，

所以

因为

∴

21. 【答案】

过作，如下图所示，

则有，

因为，

故，，即

22.解：（1）DE∥BC，理由如下：

∵∠1+∠4＝180°，∠1+∠2＝180°，

∴∠2＝∠4，

∴AB∥EF，

∴∠3＝∠5，

∵∠3＝∠B，

∴∠5＝∠B，

∴DE∥BC，

（2）∵DE平分∠ADC，

∴∠5＝∠6，

∵DE∥BC，

∴∠5＝∠B，

∵∠2＝3∠B，

∴∠2+∠5+∠6＝3∠B+∠B+∠B＝180°，

∴∠B＝36°，

∴∠2＝108°，

∵∠1+∠2＝180°，

∴∠1＝72°．

23．解：(1)AB∥CD．理由如下：如图1，延长EG交CD于点H．∴∠HGF＝∠EGF＝90°，∴∠GHF＋∠GFH＝90°．∵∠BEG＋∠DFG＝90°，∴∠BEG＝∠GHF，∴AB∥CD．

(2)∠BEG＋∠MFG＝90°．理由如下：如图2，延长EG交CD于点H．∵AB∥CD，∴∠BEG＝∠GHF．∵EG⊥FG，∴∠GHF＋∠GFH＝90°．∵∠MFG＝2∠DFG，∴∠BEG＋∠MFG＝90°．

(3)∠BEG＋∠MFG＝90°．理由如下：∵AB∥CD，∴∠BEG＝∠GHF．∵EG⊥FG，∴∠GHF＋∠GFH＝90°．∵∠MFG＝n∠DFG，∴∠BEG＋∠MFG＝90°．

24．解：利用平移线段，得地毯的长度是6.4+2.8+2.8=12（米），

∴地毯的面积是12×3=36（米2），

∴买地毯至少需要36×40=1440（元）.