初中数学2.2 切线长定理教案配套课件ppt

这是一份初中数学2.2 切线长定理教案配套课件ppt，文件包含22切线长定理课件pptx、22切线长定理练习docx、22切线长定理教案doc、22切线长定理学案docx等4份课件配套教学资源，其中PPT共21页， 欢迎下载使用。

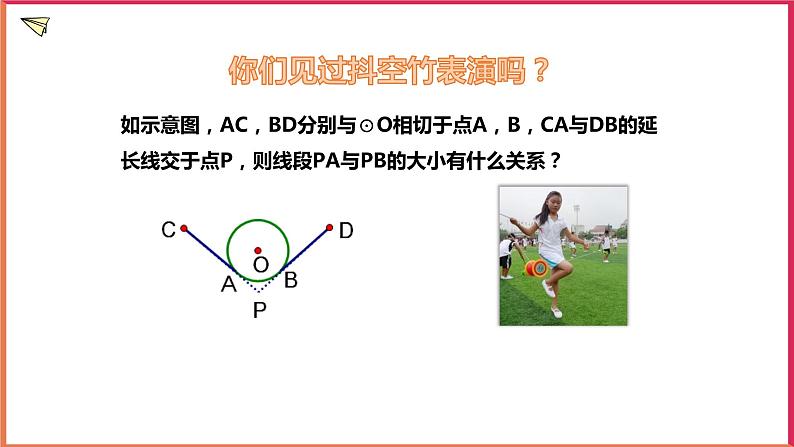
如示意图，AC，BD分别与⊙O相切于点A，B，CA与DB的延长线交于点P，则线段PA与PB的大小有什么关系？
你们见过抖空竹表演吗？
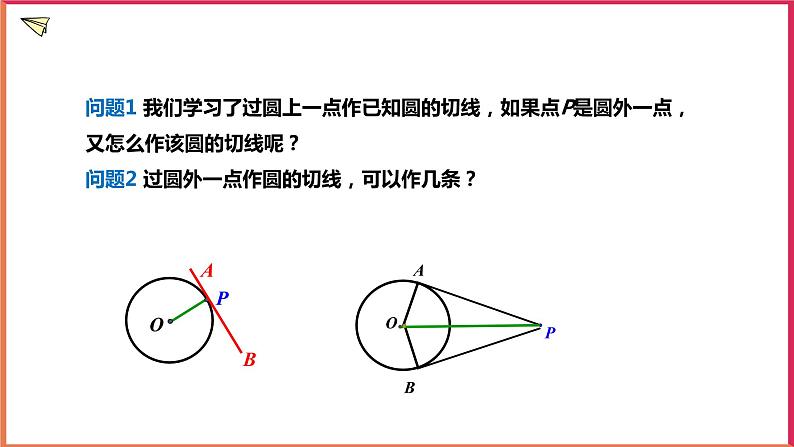
问题1 我们学习了过圆上一点作已知圆的切线，如果点P是圆外一点，又怎么作该圆的切线呢？问题2 过圆外一点作圆的切线，可以作几条？
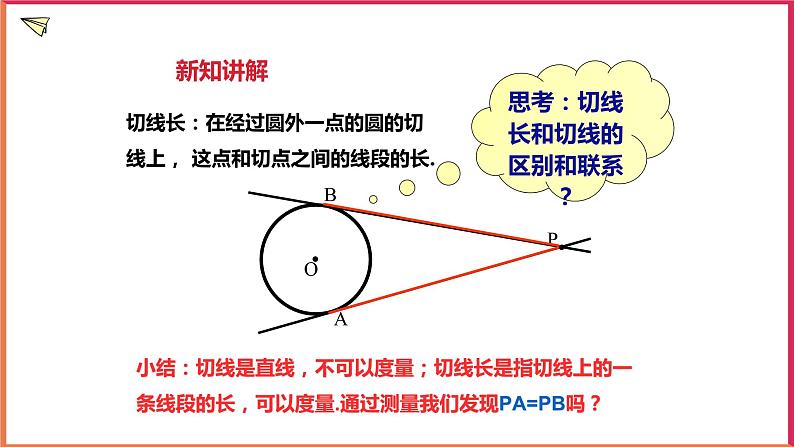
思考：切线长和切线的区别和联系？
小结：切线是直线，不可以度量；切线长是指切线上的一条线段的长，可以度量.通过测量我们发现PA=PB吗？
切线长：在经过圆外一点的圆的切线上， 这点和切点之间的线段的长.
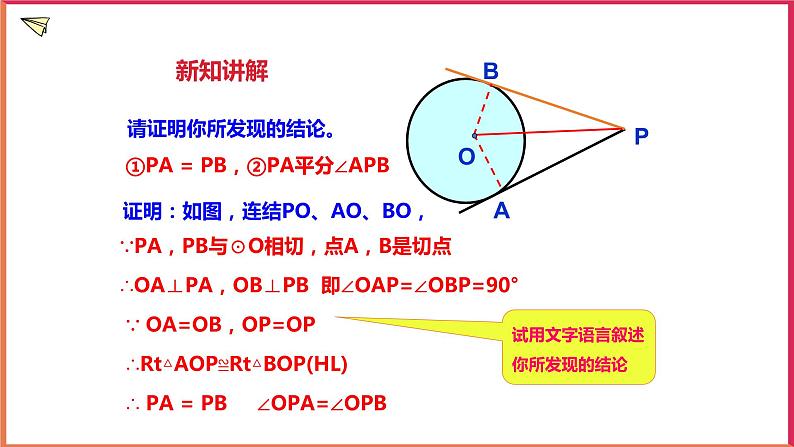
请证明你所发现的结论。
①PA = PB，②PA平分∠APB
∵PA，PB与⊙O相切，点A，B是切点∴OA⊥PA，OB⊥PB 即∠OAP=∠OBP=90° ∵ OA=OB，OP=OP ∴Rt△AOP≌Rt△BOP(HL) ∴ PA = PB ∠OPA=∠OPB
试用文字语言叙述你所发现的结论
证明：如图，连结PO、AO、BO，
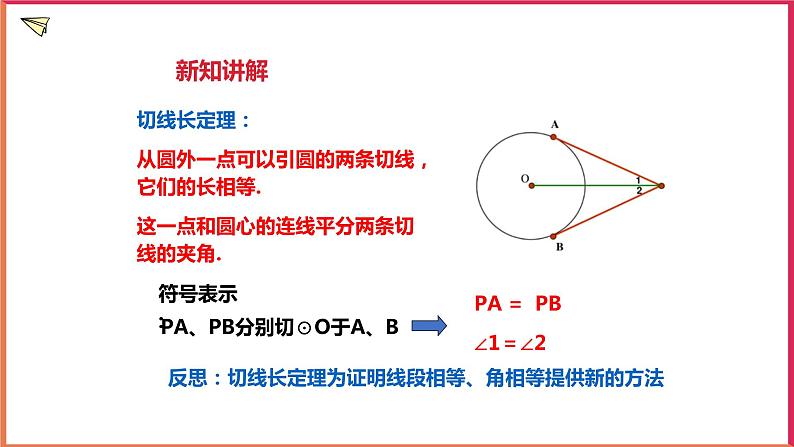
PA、PB分别切⊙O于A、B
PA = PB∠1＝∠2
切线长定理：从圆外一点可以引圆的两条切线，它们的长相等. 这一点和圆心的连线平分两条切线的夹角.
反思：切线长定理为证明线段相等、角相等提供新的方法
（2）写出图中所有相等的弧
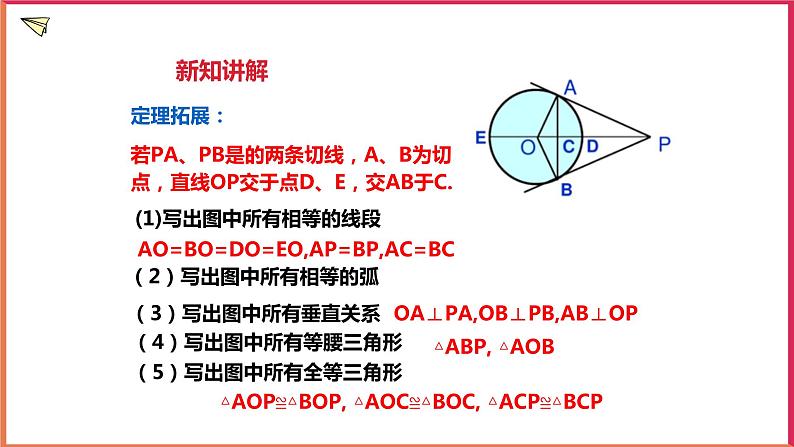
AO=BO=DO=EO,AP=BP,AC=BC
定理拓展：若PA、PB是的两条切线，A、B为切点，直线OP交于点D、E，交AB于C.
(1)写出图中所有相等的线段
（3）写出图中所有垂直关系
（4）写出图中所有等腰三角形
（5）写出图中所有全等三角形
OA⊥PA,OB⊥PB,AB⊥OP
△AOP≌△BOP, △AOC≌△BOC, △ACP≌△BCP
例1 如图，点O是 所在圆的圆心，AC，BC分别与⊙O相切于点A,B,已知∠ACB=80°.OC=102m求点C到⊙O的切线长（结果精确到1m）.
分析：对于求切线长，一般连过切点的半径，构造直角三角形，然后再解直角三角形.
∵ AC，BC分别与⊙O相切于点A,B，∴AC=BC（过圆外一点所作的圆的两条切线长相等）
答：点C到⊙O的切线长约为78 m
∴AC=OCcs40 ° =102cs40 ° ≈78(m)
在R△OAC中， ∠OAC=90 ° （为什么？）
又∵ OA＝OB，OC＝OC∴△OAC≌△OBC
解：如图,连结OA，OB
例2 如图表示皮带传动装置中一个轮子，传动皮带MA，MB分别切⊙O于点A.B延长MA,NB,相交于点P，已知∠ APB=60 °,AP=24，求两切点间的距离和 的长（精确到1）
分析：对于实际问题先抽象出几何图形，本题考查切线长，连过切点的半径，构造直角三角形，然后再解直角三角形，即可求得结果.
解：如图连结AB,OA.OB
∵MP,NP分别切⊙O于点A,B∴OA⊥AP,OB⊥BP,AP=BP(为什么？)
又∵ ∠APB=60°, ∴ △APB为等边三角形， ∴ AB=AP=24cm,
∵ OA=OB, ∴OP平分∠ APB, ∠ OPA=30°,
而∠AOB=360°-2×90°-60°=120°
答：两切点间的距离为24cm， 的长约为29cm
（1）由切线长定理 既可得到线段相等，又可以得到角相等，运用时要根据题意选用.
（2）切线长定理的基本图形要记牢，由基本图形可得到很多有用结论：
①分别连结圆心和切点，可得垂直②连结两切点，可得垂直平分③连结圆心和圆外一点，可得角相等
1、填空：如图，PA、PB分别与⊙O相切于点A、B，（1）若PB=12，PO=13，则AO= ; （2）若PO=10，AO=6，则PB= ；（3）若PA=4，AO=3，则PO= .
2.已知如图，PA、PB分别切⊙O于点A、B，∠P=60°，AP=5，则AB长为 .
分析：由切线长定理知PA=PB，根据己知条件即可判定△PAB是等边三角形，由此可求得AB的长.
解：∵PA、PB分别切 ⊙O于A、B，∴PA=PB.∵∠P=60°,∴△PAB是等边三角形；∴AB=PA=5,故答案为5.
解：由 PA,PB分别于圆O相切于点A,B，∴AO⊥PA，BO⊥PB.∴△AOP是直角三角形.在Rt△PAO中，由勾股定理得：AO²+PA²=PO²， ∵ PO=PD+AO, ∴AO²+PA²=(PD+AO)²， ∵ PA=4cm,PD=2cm，∴AO²+4²=(2+AO)²∴AO²+16=4+4AO+AO², ∴4AO=12, ∴AO=3cm答： ⊙O的半径为3cm.
3.如图，PA、PB分别与⊙O相切于点A、B，PO与⊙O相交于点D，且PA=4cm,PD=2cm.求半径OA的长.
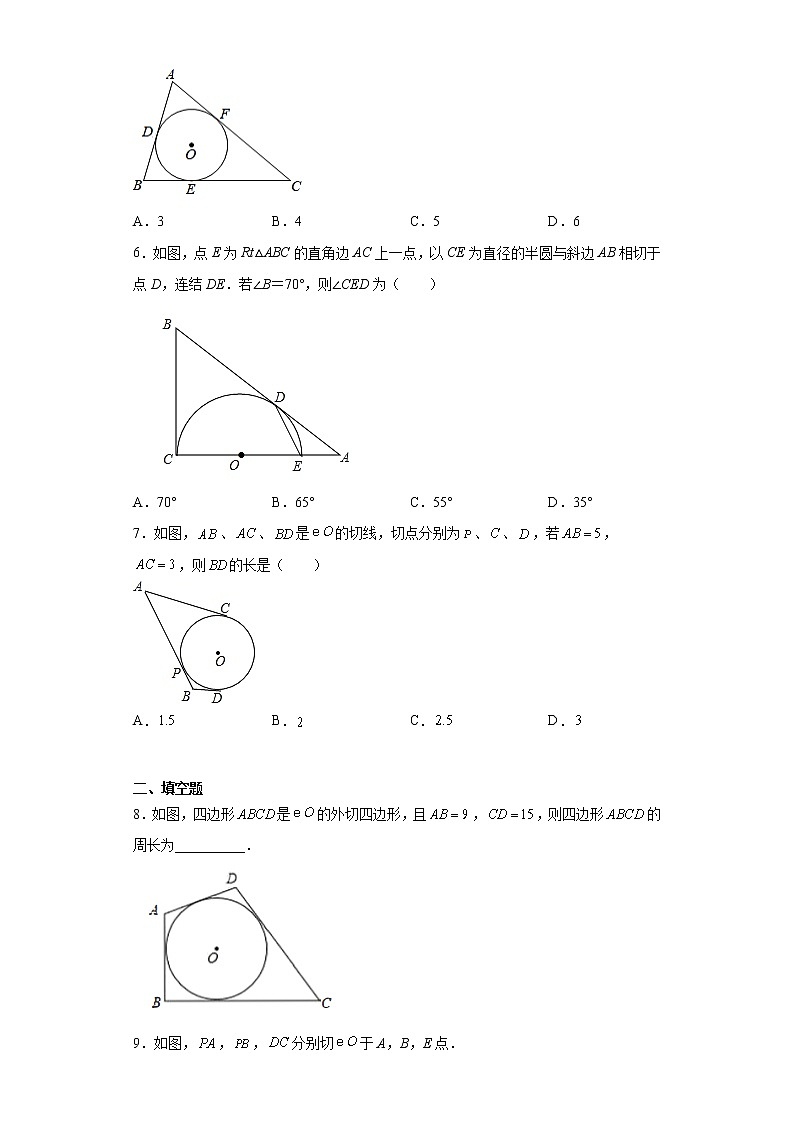
1.把直尺、三角尺和圆形螺母桉如图所示放置于桌面上，∠CAB= 60°，若量出AD=6cm，则圆形螺母的外直径是（）
【分析】设圆形螺母的圆心为O，连接OD，OE，OA，如图所示：根据切线的性质得到AO为∠ DAB的平分线，OD丄AC，又∠CAB=60°，得到∠OAE=∠OAD=0.5∠DAB=60°，根据三角函数的定义求出OD的长，即为圆的半径，进而确定出圆的直径.
∵AD，AB分别为圆O的切线，∴AO为∠DAB的平分线，OD丄AC，OD丄AC，
解：设圆形螺母的圆心为O，与AB切于E，连接OD，OE，OA，如图所示：
在Rt△AOD中，∠OAD=60°，AD=6cm，
又∠CAB=60°，∠OAE=∠OAD=0.5∠DAB=60°,
2.如图，已知AB是⊙O的直径，CD与⊙O相切于 C，BE∥CO,(1)求证:BC是∠ABE的平分线(2)若DC＝8，⊙O的半径OA＝6，求CE的长
证明：∵ DE是切线， ∴OCDE, ∵BE∥CO, ∴∠OCB=∠CBE， ∵OC=OB, ∴∠OCB=∠CBE， ∵OC=OB, ∴∠OCB=∠OBC, ∴∠CBE=∠CBO, ∴BC平分∠ABE