数学必修 第二册6.2 平面向量的运算习题

这是一份数学必修 第二册6.2 平面向量的运算习题，共11页。
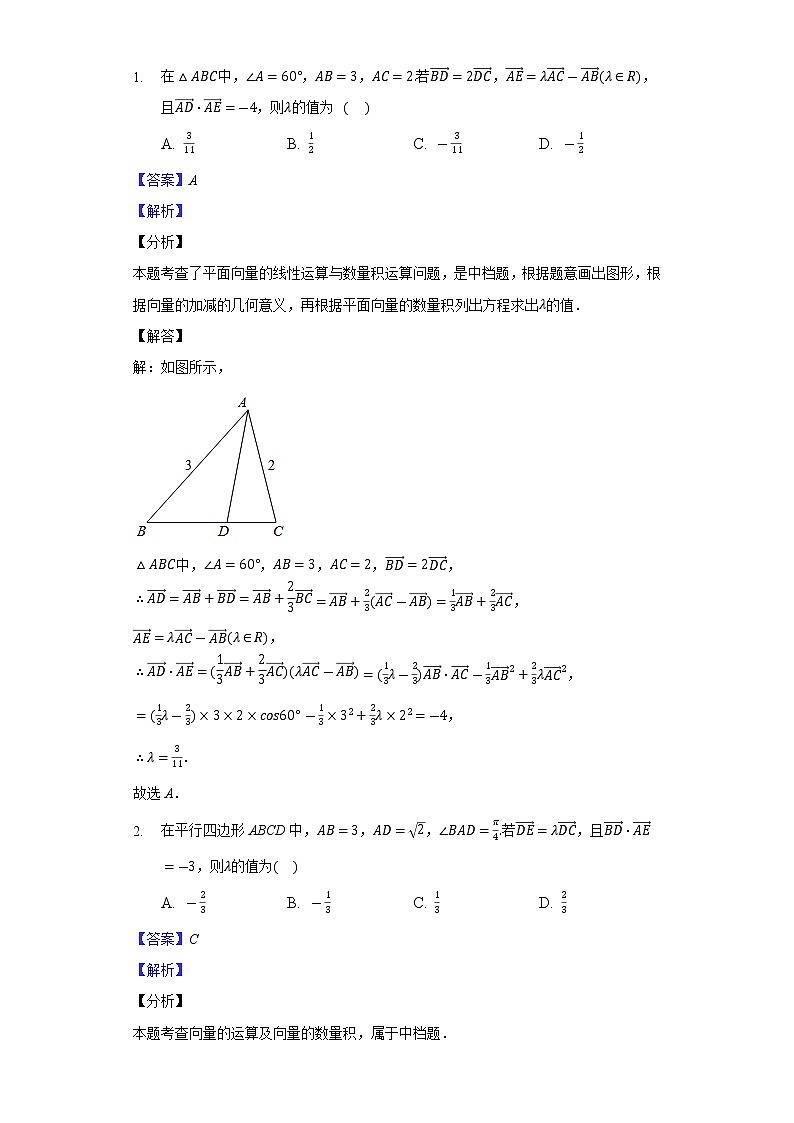
在中，，，若，，且，则的值为      A.  B.  C.  D. 【答案】A【解析】【分析】
本题考查了平面向量的线性运算与数量积运算问题，是中档题，根据题意画出图形，根据向量的加减的几何意义，再根据平面向量的数量积列出方程求出的值．
【解答】
解：如图所示，

中，，，，，
，
，
，
，
．
故选A．  在平行四边形ABCD中，，，若，且，则的值为A.  B.  C.  D. 【答案】C【解析】【分析】
本题考查向量的运算及向量的数量积，属于中档题．
结合图形可得，结合相关数据及即可求得的值．
【解答】
解：如图，，
，
因为，，．
所以
，
即．
故选C．
  已知四边形ABCD是矩形，，点E是线段AC上一点，，且，则实数的取值为A.  B.  C.  D. 【答案】B【解析】解：四边形ABCD是矩形，，
可得，
，
点E是线段AC上一点，，且，
可得，
即有，
解得，
故选：B．
由矩形可得，，再由向量的加减运算和向量数量积的性质计算可得所求值．
本题考查向量的加减运算和数量积的性质，属于基础题．
 在平行四边形ABCD中，，，，，，则A.  B.  C.  D. 【答案】B【解析】【分析】
本题考查向量的加减运算以及向量的数量积，根据向量的加减的几何意义和向量的数量积即可求出．
【解答】
解：因为
，解得．
故选B．  在菱形ABCD中，已知，点E、F满足，，若，则实数的值为A.  B. 2 C. 3 D. 4【答案】B【解析】【分析】
本题考查了向量的加法、减法、数乘运算和向量的数量积，属于中档题．
利用向量的加法、减法、数乘运算，结合题目条件得和，再利用向量的数量积，结合题目条件，计算得结论．
【解答】
解：因为在菱形ABCD中，，点E、F满足，，
所以，，
因此
，
．
又因为
所以，
因此
即，
所以，解得．
故选B．  已知的内角A，B，C的对边分别为a，b，c，且满足，，，O为的外心．若，则的值为   A.  B. 2 C.  D. 3【答案】A【解析】【分析】
本题考查向量的数量积运算，属中档题．
根据及，得到关于m，n的关系式，同理可得，由此可得m，n的值，从而得到最后结果．
【解答】
解：由题意得，
，
又，
所以，
即，即，
同理，
又，
所以，
即即，
由得．
故选A．  在中，，，，点M满足，若，则的值为________．【答案】【解析】解析：由于，，，则，因为，则，即，又，因此，因此．
 在中，已知，，，若点P满足，且，则实数的值为__________．【答案】或1【解析】【分析】
本题考查平面向量的数量积运算与线性表示的应用问题，也考查了运算推理能力，属于基础题．
根据题意，利用平面向量的线性运算，把、用、与表示出来，再求即可．
【解答】
解：中，，，，
点P满足，
，
；
又，
，
，
整理得，
解得或，
实数的值为或1．  已知矩形ABCD中，，，若点P满足，且，则的值是________．【答案】或2【解析】【分析】
本题主要考查平面向量的线性运算、数量积等，考查考生的运算求解能力．
先由题意将转化为，再由建立关于的二次方程，解之可得答案．
【解答】
解：因为，所以．
又
，
所以
，
即，所以或．
故答案为或2．  若正方形ABCD的边长为，若，则的值为______．【答案】【解析】解：正方形ABCD的边长为，作图如下：

，
，
，
解得：，
故答案为：．
作出图形，依题意得：，，于是，可解得的值．
本题考查平面向量数量积的运算，考查平面向量基本定理的应用，考查作图能力与运算能力，属于中档题．
 在等腰梯形ABCD中，，，，，若，，且，则实数的值为______．【答案】【解析】【分析】
本题考查向量在几何中的应用，属中档题根据数量积的定义把展开，
得到
．
求解．
【解答】
解：依题意得，，
．

因为，
，
因为，
所以
，
，
，
解得，
故答案为．  在中，，，，D是BC中点，E在边AC上，，，则________，的值为________．【答案】；【解析】【分析】本题考查了向量的加法、减法、数乘运算，向量的数量积，向量的夹角，考查了运算求解能力与转化化归思想，属于中档题．由，结合平面向量数量积的运算即可得；由可得，再由平面向量数量积的运算即可得．【解答】
解：因为，，，所以，由题意，，所以，所以；由可得，解得．故答案为：；．  已知菱形ABCD的边长为2，，点E、F分别在直线BC、DC上，，若，则实数的值为__________________．【答案】【解析】【分析】
本题考查平面向量数量积的运算，属于中档题．
利用向量的加减法法则以、作为基底表示出、，根据，通过向量数量积的运算，得到的方程，解得的值即可．
【解答】
解：，
所以
，
解得．
故答案为．  3．如图所示，直角坐标系中网格小正方形的边长为1，若向量，，满足，则___________.【答案】【分析】由向量的基本定理，由图知，，，结合已知条件及向量的运算性质即可求的值.【详解】若设x轴、y轴方向上单位向量分别为，∴由图知：，，，又∵，得，∴.故答案为：.6．在中，，，，点，在边上且，.（1）若，求的长；（2）若，求的值.【答案】（1）；（2）.【分析】（1）先设，，根据题意，求出，，再由向量模的计算公式，即可得出结果；（2）先由题意，得到，，再由向量数量积的运算法则，以及题中条件，得到，即可求出结果.【详解】（1）设，，则，，因此，所以，，（2）因为，所以， 同理可得，，所以，∴，即， 同除以可得，.【点睛】本题主要考查用向量的方法求线段长，考查由向量数量积求参数，熟记平面向量基本定理，以及向量数量积的运算法则即可，属于常考题型.