北师大版初中数学八年级下册期中测试卷

这是一份北师大版初中数学八年级下册期中测试卷，共20页。试卷主要包含了选择题，填空题，计算题等内容，欢迎下载使用。
 北师大版初中数学八年级下册期中测试卷考试范围：第一.二.三章；考试时间：120分钟；总分：100分学校:___________姓名：___________班级：___________考号：___________注意：本试卷包含Ⅰ、Ⅱ两卷。第Ⅰ卷为选择题，所有答案必须用2B铅笔涂在答题卡中相应的位置。第Ⅱ卷为非选择题，所有答案必须填在答题卷的相应位置。答案写在试卷上均无效，不予记分。 第I卷（选择题） 一、选择题（本大题共12小题，共36.0分）如图，是的角平分线，于点，于点，，，，则的长是A.
B.
C.
D. 如图，在中，的垂直平分线交于点，交于点，连接若，，则的周长为A.
B.
C.
D. 如图，已知，，，以，两点为圆心，大于的长为半径画圆弧，两弧相交于点，，连接与相交于点，则的周长为A.
B.
C.
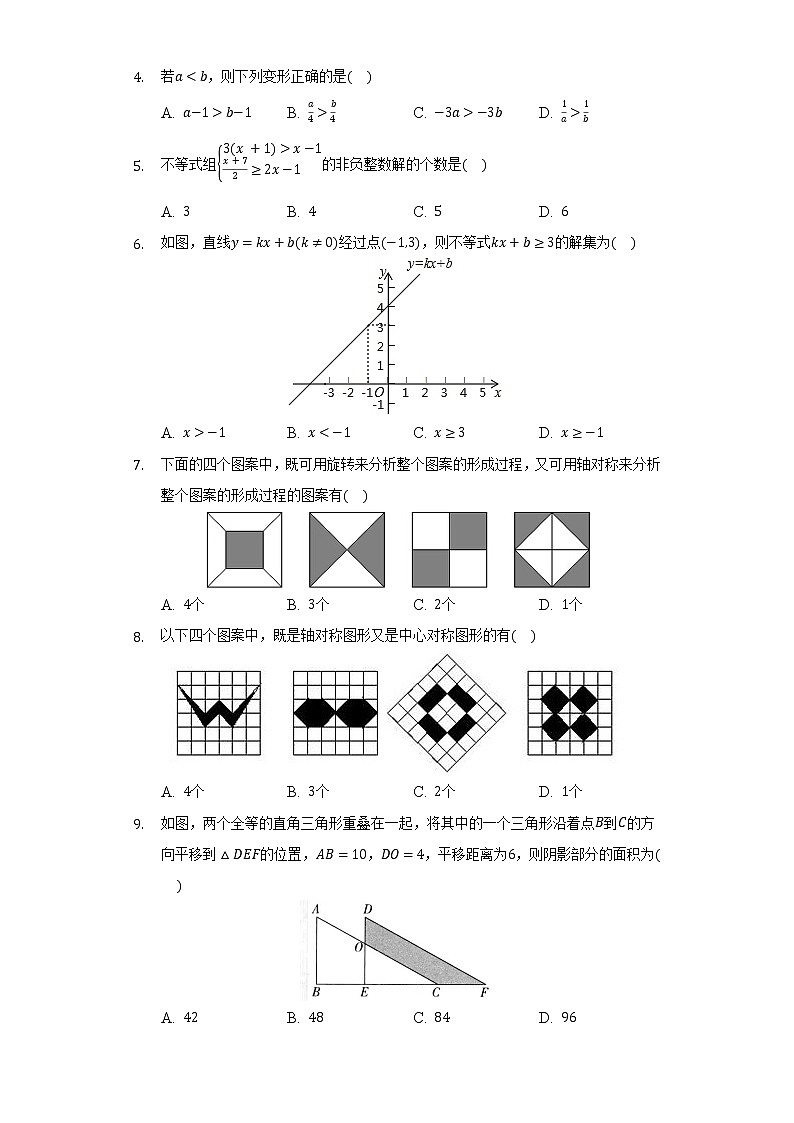
D. 若，则下列变形正确的是A.  B.  C.  D. 不等式组的非负整数解的个数是A.  B.  C.  D. 如图，直线经过点，则不等式的解集为
A.  B.  C.  D. 下面的四个图案中，既可用旋转来分析整个图案的形成过程，又可用轴对称来分析整个图案的形成过程的图案有
A. 个 B. 个 C. 个 D. 个以下四个图案中，既是轴对称图形又是中心对称图形的有
A. 个 B. 个 C. 个 D. 个如图，两个全等的直角三角形重叠在一起，将其中的一个三角形沿着点到的方向平移到的位置，，，平移距离为，则阴影部分的面积为   
A.  B.  C.  D. 现规定一种新运算，，其中、为常数，若，则不等式的解集是A.  B.  C.  D. 符号为不超过的最大整数，如，对于任意实数，下列式子中错误的是A.  B.
C.  D. 有不足个苹果分给若干个小朋友，若每个小朋友分个，则剩个苹果；若每个小朋友分个，则有一个小朋友没分到苹果，且最后一个分到苹果的小朋友分得的苹果数不足个．已知小朋友人数是偶数个，那么苹果的个数是A.  B.  C.  D. 第II卷（非选择题） 二、填空题（本大题共4小题，共12.0分）若关于的不等式组的解集为，则的值为      ．如图，长方形中，，，对角线的垂直平分线分别交，于点，，连接，则的长为________．不等式组的解集为______．直线：与直线：在同一平面直角坐标系中的图象如图所示，则关于的不等式的解集为______．
   三、计算题（本大题共8小题，共52.0分）在中，平分，是上一点，，交于交的延长线于，交的延长线于解答以下问题．
求证：是等腰三角形；
试在图中找出一对全等的三角形并给予证明；
试猜想与的大小有什么关系？并证明你的猜想．






 如图，在中，，，，动点、同时从、两点出发，分别在、边上匀速移动，它们的速度分别为，，当点到达点时，、两点同时停止运动，设点的运动时间为．
当为何值时，为等边三角形？
当为何值时，为直角三角形？






 如图，，于，交的延长线于，且．
与是否相等？请说明理由；
若，，则的长为______．
  






 解不等式组并写出它的正整数解．






 我市在创建全国文明城市过程中，决定购买，两种树苗对某路段道路进行绿化改造，已知购买种树苗棵，种树苗棵，需要元；若购买种树苗棵，种树苗棵，则需要元．求，两种树苗每棵各多少元？考虑到绿化效果和资金周转，购进种树苗不能少于棵，且用于购买这两种树苗的资金不能超过元，若购进这两种树苗共棵，则有哪几种购买方案？某包工队承包种植任务，若种好一棵种树苗可获工钱元，种好一棵种树苗可获工钱元，在第问的购买方案中，种好这棵树苗，哪一种购买方案所付的种植工钱最少？最少工钱是多少元？






 岳阳市南县大力发展农村旅游事业，全力打造“洞庭之心湿地公园”，其中罗文村的“花海、涂鸦、美食”特色游享誉三湘，游人如织．去年村民罗南洲抓住机遇，返乡创业，投入万元创办农家乐餐饮住宿，一年时间就收回投资的，其中餐饮利润是住宿利润的倍还多万元．
求去年该农家乐餐饮和住宿的利润各为多少万元；
今年罗南洲把去年的餐饮利润全部用于继续投资，增设了土特产的实体店销售和网上销售项目．他在接受记者采访时说：“我预计今年餐饮和住宿的利润比去年会有的增长，加上土特产销售的利润，到年底除收回所有投资外，还将获得不少于万元的纯利润．”请问今年土特产销售至少有多少万元的利润？






 如图，含有的直角三角板，，，将绕着点逆时针旋转，得到，使得点落在边上的点处，过点的直线，求的度数．







 如图，在正方形中，，用一块含的三角板，把角的顶点放在点，将三角板绕着点旋转，使这个角的两边与线段、分别相交于点、．
  由几个不同的位置，分别测量、、的长，从中你能发现、、的数量之 间具有怎样的关系？并证明你所得到的结论；
 设，，求与之间的函数解析式，并写出自变量的取值范围．







答案和解析 1.【答案】
 【解析】【分析】本题主要考查了角平分线的性质；利用三角形的面积求线段的大小是一种很好的方法，要注意掌握应用．
由是的平分线推出，结合三角形面积公式求出答案．【解答】解：是中的平分线，于点，交于点，
．
又，，
，
．
故选D．
   2.【答案】
 【解析】【分析】
本题考查了线段垂直平分线的性质：垂直平分线垂直且平分其所在线段；垂直平分线上任意一点，到线段两端点的距离相等．
在中，的垂直平分线交于点，交于点，连接若，，则的周长为．
【解答】
解：垂直平分，
，
的周长



．
故选：．  3.【答案】
 【解析】【分析】
本题考查了作图基本作图：熟练掌握基本作图作一条线段等于已知线段；作一个角等于已知角；作已知线段的垂直平分线；作已知角的角平分线；过一点作已知直线的垂线也考查了线段垂直平分线的性质．
利用基本作图得到垂直平分，利用线段垂直平分线的定义得到，然后利用等线段代换得到的周长．
【解答】
解：由作法得垂直平分，
，
的周长．
故选：．  4.【答案】
 【解析】【分析】
本题考查了不等式的性质，能熟记不等式的性质的内容是解此题的关键．
根据不等式的性质逐个判断即可．
【解答】
解：、，
，故本选项不符合题意；
B、，
，故本选项不符合题意；
C、，
，故本选项符合题意；
D、若，则不一定成立，比如，，但，故本选项不符合题意；
故选：．  5.【答案】
 【解析】解：，
解得：，
解得，
则不等式组的解集为．
故非负整数解为，，，，共个
故选：．
先求出不等式组的解集，在取值范围内可以找到整数解．
本题考查不等式组的解法及整数解的确定．解不等式组应遵循以下原则：同大取较大，同小取较小，大小小大中间找，大大小小解不了．
 6.【答案】
 【解析】解：观察图象知：当时，，
故选：．
结合函数的图象利用数形结合的方法确定不等式的解集即可．
本题考查了一次函数与一元一次不等式的知识，解题的关键是根据函数的图象解答，难度不大．
 7.【答案】
 【解析】【分析】
本题考查了旋转和轴对称的性质．旋转变化前后，对应线段、对应角分别相等，图形的大小、形状都不改变，两组对应点连线的交点是旋转中心；轴对称图形的对应线段、对应角相等．
图形的旋转是图形上的每一点在平面上绕某个固定点旋转固定角度的位置移动；轴对称是指如果一个图形沿一条直线折叠，直线两侧的图形能够互相重合，就是轴对称，据此解答即可．
【解答】
解：图形可以旋转得到，也可以经过轴对称，沿一条直线对折，能够完全重合；
图形可以旋转得到，也可以经过轴对称，沿一条直线对折，能够完全重合；
图形可以旋转得到，也可以经过轴对称，沿一条直线对折，能够完全重合；
图形可以旋转得到，也可以经过轴对称，沿一条直线对折，能够完全重合．
故既可用旋转来分析整个图案的形成过程，又可用轴对称来分析整个图案的形成过程的图案有个．
故选：．  8.【答案】
 【解析】【分析】
本题考查了轴对称图形和中心对称图形，掌握好中心对称图形与轴对称图形的概念是解题的关键．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，图形旋转度后与原图重合．
根据轴对称图形与中心对称图形的概念求解．
【解答】
解：图是轴对称图形不是中心对称图形；
图、、既是轴对称图形，又是中心对称图形．
故选B．
  9.【答案】
 【解析】由题意可知，，，
，
，，
，
故选B．
 10.【答案】
 【解析】【分析】
本题考查了新定义及解一元一次不等式：先去分母和括号，再移项、合并，然后把未知数的系数化为得到不等式的解集．也考查了阅读理解能力．
先根据新定义得到，解得，则不等式化为，然后通过去分母、移项可得到不等式的解集．
【解答】
解：，，
，
，
，
去分母得，
移项并合并得，
系数化为得．
故选B．  11.【答案】
 【解析】略
 12.【答案】
 【解析】【分析】
本题考查了一元一次不等式组的应用，根据各数量之间的关系，正确列出一元一次不等式组是解题的关键．
设小朋友的人数为人，则苹果的个数为个，根据“若每个小朋友分个，则有一个小朋友没分到苹果，且最后一个分到苹果的小朋友分得的苹果数不足个”，即可得出关于的一元一次不等式组，解之即可得出的取值范围，结合为偶数即可得出的值，再将其代入中即可求出结论．
【解答】
解：设小朋友的人数为人，则苹果的个数为个，
依题意，得：，
解得：．
又为偶数，
，
．
故选B．  13.【答案】
 【解析】略
 14.【答案】
 【解析】【分析】本题考查的是线段垂直平分线的性质．关键是要设所求的量为未知数利用勾股定理求解．本题首先利用线段垂直平分线的性质推出≌，再利用勾股定理即可求解．【解答】解：垂直且平分，故AE，．
所以≌．
设为．
则，．
根据勾股定理可得，
解得．
故答案为．  15.【答案】
 【解析】解：解不等式，得：，
解不等式，得：，
则不等式组的解集为，
故答案为：．
分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集．
本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
 16.【答案】
 【解析】【分析】
观察函数图象可知，当时，函数图象都在函数的图象上方，从而可得到关于的不等式的解集．
【解答】
解：由图知，当时，
所以不等式的解集为．
故答案为．  17.【答案】证明：，
，，
平分，
，
，
，
是等腰三角形．

≌．
证明：，
两直线平行，内错角相等，两直线平行，内错角相等，
又已知，
；
，
在和中，
，
≌．

，
理由：平分，
，
，
，
，
，
≌，
，
，
为等腰三角形，
，
，即．
 【解析】由平行线，可得同位角、内错角相等，即，，进而再由平分线的性质以及角之间的转化，即可得出结论；
可由两角夹一边求解≌；
在的基础上可得出线段之间的关系，通过等量代换即可．
本题主要考查了平行线的性质以及全等三角形的判定及性质和等腰三角形的判定问题，能够熟练掌握并运用．
 18.【答案】解：在中，，，
．
，
，，．
当时，为等边三角形．
即．
．
当时，为等边三角形；
若为直角三角形，
当时，，
即，
．
当时，，
即，
．
即当或时，为直角三角形．
 【解析】用含的代数式表示出、．
由于，当时，可得到关于的一次方程，求解即得结论；
分两种情况进行讨论：当时，当时．利用直角三角形中，含角的边间关系，得到关于的一次方程，求解得结论．
本题考查了含角的直角三角形、等边三角形以及分类讨论的思想方法，利用“直角三角形中，角所对的边等于斜边的一半”及“有一个角是的等腰三角形是等边三角形”，得到关于的一次方程是解决本题的关键．
 19.【答案】
 【解析】解：，
证明：，于，于，
．
在和中，
≌．
．
在与中
，
≌，
，，
．
故答案为：．
首先利用角平分线的性质求出，再根据斜边直角边证明≌，推的；
利用证明≌，推，，最后求出长．
本题考查了全等三角形的判定与性质、角平分线的性质，熟练掌握全等三角形的判定方法与性质，角平分线的性质应用是解题关键．
 20.【答案】解：不等式组的正整数解是，．
 【解析】略
 21.【答案】解：设种树苗每棵元，种树苗每棵元，
根据题意，得：，
解得：，
答：种树苗每棵元，种树苗每棵元；

设购进种树苗棵，则购进种树苗棵，
根据题意，得：，
解得：，
所以购买的方案有：
、购进种树苗棵，种树苗棵；
、购进种树苗棵，种树苗棵；

方案一的费用为元，
方案二的费用为元，
所以购进种树苗棵，种树苗棵所付工钱最少，最少工钱为元．
 【解析】设种树苗每棵元，种树苗每棵元，根据“购买种树苗棵，种树苗棵，需要元；若购买种树苗棵，种树苗棵，则需要元”列二元一次方程组求解可得；
设购进种树苗棵，则购进种树苗棵，根据“种树苗不能少于棵，且用于购买这两种树苗的资金不能超过元”列不等式组求解可得；
根据中所得方案，分别计算得出费用即可．
本题主要考查一元一次不等式组、二元一次方程组的应用，解题的关键是仔细审题，找到题目蕴含的相等或不等关系得出方程组、不等式组．
 22.【答案】解：设去年餐饮利润万元，住宿利润万元，
依题意得：，
解得：，
答：去年餐饮利润万元，住宿利润万元；
设今年土特产利润万元，
依题意得：，
解之得，，
答：今年土特产销售至少有万元的利润．
 【解析】设去年餐饮利润为万元，住宿利润为万元，根据题意列出方程组，求出方程组的解即可得到结果；
设今年土特产的利润为万元，根据题意列出不等式，求出不等式的解集即可得到结果．
此题考查了一元一次不等式的应用，以及二元一次方程组的应用，弄清题中的不等及相等关系是解本题的关键．
 23.【答案】解：中，，，
，
绕着点逆时针旋转，得到，
，
是等边三角形，
，
，
，
，
，
，
，
．
 【解析】首先根据直角的性质求出，利用旋转的性质求出是等边三角形，进而求出，再利用平行线的性质得到，结合，即可求出的度数．
本题主要考查了旋转的性质的知识，解答本题的关键是求出，利用平行线的性质即可解题，此题难度不大．
 24.【答案】解：．
理由：如图所示：延长至，使，连接，
，，，
≌，
，，
，
≌，
；

如图所示，已知，，则，，

由可知，
在中，由勾股定理，得
，即，
解得：．
 【解析】延长至，使，连接，利用旋转法证明≌，根据已知证明，可证≌，再根据全等三角形的性质可得；
由的结论，将条件集中在中，由勾股定理建立、的函数关系式．
本题考查了旋转法在证题中的运用，勾股定理在建立函数关系式中的运用．关键是通过旋转，将条件相对集中．