高中数学人教B版 (2019)必修 第一册2.2.3 一元二次不等式的解法学案

最新课程标准：从函数观点看一元二次不等式．①经历从实际情境中抽象出一元二次不等式的过程，了解一元二次不等式的现实意义．能借助一元二次函数求解一元二次不等式，并能用集合表示一元二次不等式的解集．②借助一元二次函数的图像，了解一元二次不等式与相应函数、方程的联系.

知识点　二次函数与一元二次方程、不等式的解

的对应关系

　一元二次不等式的解法：

(1)图像法：一般地，当a>0时，解形如ax2＋bx＋c>0(≥0)或ax2＋bx＋c<0(≤0)的一元二次不等式，一般可分为三步：

①确定对应方程ax2＋bx＋c＝0的解；②画出对应函数y＝ax2＋bx＋c的图像简图；③由图像得出不等式的解集．

对于a<0的一元二次不等式，可以直接采取类似a>0时的解题步骤求解；也可以先把它化成二次项系数为正的一元二次不等式，再求解．

(2)代数法：将所给不等式化为一般式后借助分解因式或配方求解，当p<q时，若(x－p)(x－q)>0，则x>q或x<p；若(x－p)(x－q)<0，则p<x<q.有口诀如下“大于取两边，小于取中间”．

[基础自测]

1．下列不等式中是一元二次不等式的是(　　)

A．a2x2＋2≥0      B.<3

C．－x2＋x－m≤0  D．x3－2x＋1>0

解析：选项A中，a2＝0时不符合；选项B是分式不等式；选项D中，最高次数为三次；只有选项C符合．

答案：C

2．不等式x(x＋1)≤0的解集为(　　)

A．[－1，＋∞)  B．[－1,0)

C．(－∞，－1]  D．[－1,0]

解析：解不等式得－1≤x≤0，故选D.

答案：D

3．函数y＝的定义域为(　　)

A．[－7,1] 

B．(－7,1)

C．(－∞，－7]∪[1，＋∞) 

D．(－∞，－7)∪(1，＋∞)

解析：由7－6x－x2>0，得x2＋6x－7<0，即(x＋7)(x－1)<0，所以－7<x<1，故选B.

答案：B

4．不等式1＋2x＋x2≤0的解集为________．

解析：不等式1＋2x＋x2≤0化为(x＋1)2≤0，解得x＝－1.

答案：{－1}

题型一　解不含参数的一元二次不等式[教材P65例1　P66例3、例4]

例1　(1)求不等式x2－x－2>0的解集．

(2)求不等式x2－6x－1≤0的解集．

(3)求不等式－x2＋2x－1<0的解集．

【解析】　(1)因为x2－x－2＝(x＋1)(x－2)，

所以原不等式等价于(x＋1)(x－2)>0，因此所求解集为(－∞，－1)∪(2，＋∞)．

(2)因为x2－6x－1＝x2－6x＋9－9－1＝(x－3)2－10，

所以原不等式可化为(x－3)2－10≤0，即(x－3)2≤10，

两边开平方得|x－3|≤，从而可知－≤x－3≤，

因此3－≤x≤3＋，所以不等式的解集为[3－，3＋]．

(3)原不等式可化为x2－2x＋1>0，

又因为x2－2x＋1＝(x－1)2，所以上述不等式可化为

(x－1)2>0.

注意到只要x≠1，上述不等式就成立，所以不等式的解集为(－∞，1)∪(1，＋∞).

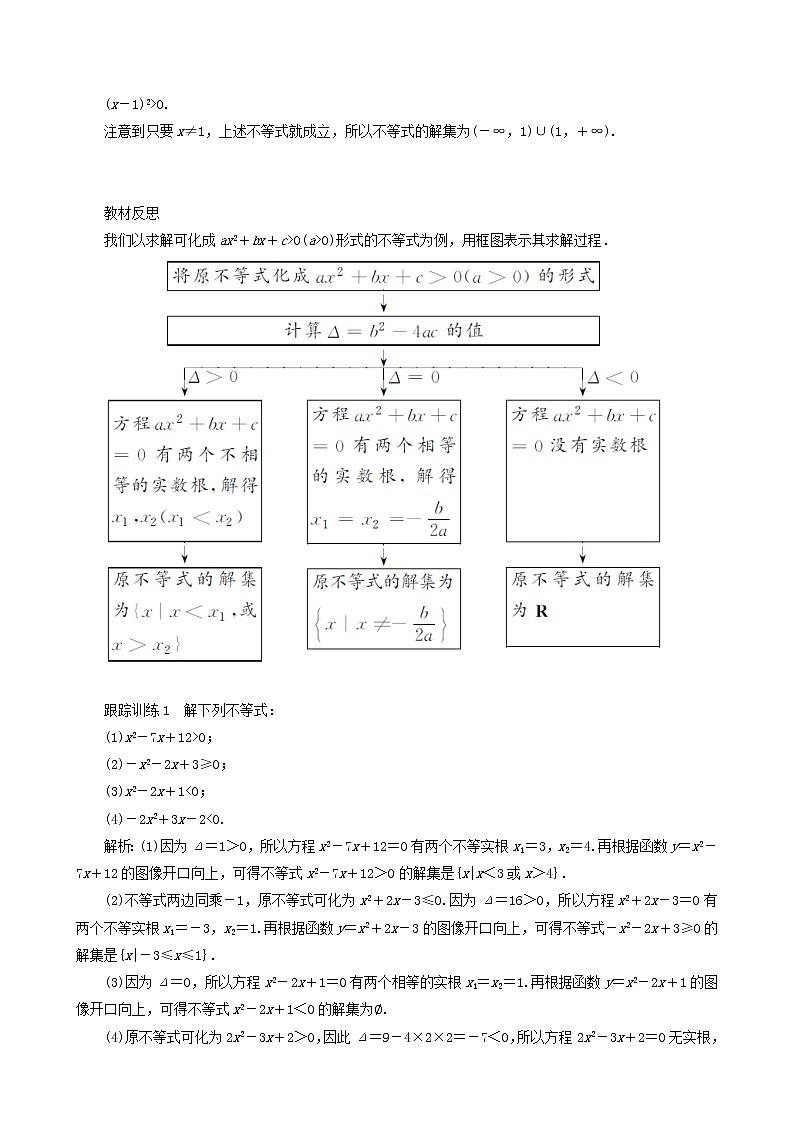
教材反思

我们以求解可化成ax2＋bx＋c>0(a>0)形式的不等式为例，用框图表示其求解过程．

跟踪训练1　解下列不等式：

(1)x2－7x＋12>0；

(2)－x2－2x＋3≥0；

(3)x2－2x＋1<0；

(4)－2x2＋3x－2<0.

解析：(1)因为Δ＝1＞0，所以方程x2－7x＋12＝0有两个不等实根x1＝3，x2＝4.再根据函数y＝x2－7x＋12的图像开口向上，可得不等式x2－7x＋12＞0的解集是{x|x＜3或x＞4}．

(2)不等式两边同乘－1，原不等式可化为x2＋2x－3≤0.因为Δ＝16＞0，所以方程x2＋2x－3＝0有两个不等实根x1＝－3，x2＝1.再根据函数y＝x2＋2x－3的图像开口向上，可得不等式－x2－2x＋3≥0的解集是{x|－3≤x≤1}．

(3)因为Δ＝0，所以方程x2－2x＋1＝0有两个相等的实根x1＝x2＝1.再根据函数y＝x2－2x＋1的图像开口向上，可得不等式x2－2x＋1＜0的解集为∅.

(4)原不等式可化为2x2－3x＋2＞0，因此Δ＝9－4×2×2＝－7＜0，所以方程2x2－3x＋2＝0无实根，又二次函数y＝2x2－3x＋2的图像开口向上，所以原不等式的解集为R.

　―→

题型二　三个“二次”之间的关系[经典例题]

例2　已知关于x的不等式ax2＋bx＋c>0的解集为{x|2<x<3}，求关于x的不等式cx2＋bx＋a<0的解集．

【解析】　方法一　由不等式ax2＋bx＋c>0的解集为{x|2<x<3}可知，a<0，且2和3是方程ax2＋bx＋c＝0的两根，由根与系数的关系可知＝－5，＝6.由a<0知c<0，＝，故不等式cx2＋bx＋a<0，即x2＋x＋>0，即x2－x＋>0，解得x<或x>，所以不等式cx2＋bx＋a<0的解集为∪.

方法二　由不等式ax2＋bx＋c>0的解集为{x|2<x<3}可知，a<0，且2和3是方程ax2＋bx＋c＝0的两根，所以ax2＋bx＋c＝a(x－2)(x－3)＝ax2－5ax＋6a⇒b＝－5a，c＝6a，故不等式cx2＋bx＋a<0，即6ax2－5ax＋a<0⇒6a<0，故原不等式的解集为∪.

　→→

→→

方法归纳

一元二次不等式与其对应的函数与方程之间存在着密切的联系，在解决具体的数学问题时，要注意三者之间的相互联系，并在一定条件下相互转换．

(1)若一元二次不等式的解集为区间的形式，则区间的端点值恰是对应一元二次方程的根，要注意解集的形式与二次项系数的联系．

(2)若一元二次不等式的解集为R或∅，则问题可转化为恒成立问题，此时可以根据二次函数图像与x轴的交点情况确定判别式的符号，进而求出参数的范围．

跟踪训练2　已知一元二次不等式x2＋px＋q<0的解集为，求不等式qx2＋px＋1>0的解集．

解析：因为x2＋px＋q<0的解集为，所以x1＝－与x2＝是方程x2＋px＋q＝0的两个实数根，

由根与系数的关系得解得

所以不等式qx2＋px＋1>0即为－x2＋x＋1>0，

整理得x2－x－6<0，解得－2<x<3.

即不等式qx2＋px＋1>0的解集为{x|－2<x<3}．

　→→→

题型三　含参数的一元二次不等式的解法[经典例题]

例3　解关于x的不等式2x2＋ax＋2>0.

【解析】　对于方程2x2＋ax＋2＝0，其判别式Δ＝a2－16＝(a＋4)(a－4)．

①当a>4或a<－4时，Δ>0，方程2x2＋ax＋2＝0的两根为x1＝(－a－)，x2＝(－a＋)．

∴原不等式的解集为

.

②当a＝4时，Δ＝0，方程有两个相等实根，x1＝x2＝－1，

∴原不等式的解集为{x|x≠－1}．

③当a＝－4时，Δ＝0，方程有两个相等实根，x1＝x2＝1，

∴原不等式的解集为{x|x≠1}．

④当－4<a<4时，Δ<0，方程无实根，∴原不等式的解集为R.

　二次项系数为2，Δ＝a2－16不是一个完全平方式，故不能确定根的个数，因此需对判别式Δ的符号进行讨论，确定根的个数.

方法归纳

含参数一元二次不等式求解步骤

(1)讨论二次项系数的符号，即相应二次函数图像的开口方向；

(2)讨论判别式的符号，即相应二次函数图像与x轴交点的个数；

(3)当Δ>0时，讨论相应一元二次方程两根的大小；

(4)最后按照系数中的参数取值范围，写出一元二次不等式的解集．

跟踪训练3　解关于x的不等式x2－(a＋a2)x＋a3>0.

解析：原不等式可变形为(x－a)·(x－a2)>0，则方程(x－a)(x－a2)＝0的两个根为x1＝a，x2＝a2，

(1)当a<0时，有a<a2，∴x<a或x>a2，此时原不等式的解集为{x|x<a或x>a2}；

(2)当0<a<1时，有a>a2，即x<a2或x>a，此时原不等式的解集为{x|x<a2或x>a}；

(3)当a>1时，有a2>a，即x<a或x>a2，此时原不等式的解集为{x|x<a或x>a2}；

(4)当a＝0时，有x≠0；∴原不等式的解集为{x|x∈R且x≠0}；

(5)当a＝1时，有x≠1，此时原不等式的解集为{x|x∈R且x≠1}；

综上可知：

当a<0或a>1时，原不等式的解集为{x|x<a或x>a2}；

当0<a<1时，原不等式的解集为{x|x<a2或x>a}；

当a＝0时，原不等式的解集为{x|x∈R且x≠0}；

当a＝1时，原不等式的解集为{x|x∈R且x≠1}．

　→→

→

题型四　一元二次不等式的实际应用[经典例题]

例4　某工厂的固定成本为3万元，该工厂每生产100台某产品的生产成本为1万元，设生产该产品x(百台)，其总成本为g(x)万元(总成本＝固定成本＋生产成本)，并且销售收入r(x)满足r(x)＝

假定该产品产销平衡，根据上述统计规律求：

(1)要使工厂有盈利，产品数量x应控制在什么范围？

(2)工厂生产多少台产品时盈利最大？

【解析】　(1)依题意得g(x)＝x＋3，设利润函数为f(x)，则

f(x)＝r(x)－g(x)，所以f(x)＝

要使工厂有盈利，则有f(x)>0，因为f(x)>0⇒或⇒

或⇒或则3＜x≤7或7＜x＜10.5，即3＜x＜10.5，所以要使工厂盈利，产品数量应控制在大于300台小于1 050台的范围内．

(2)当3＜x≤7时，f(x)＝－0.5(x－6)2＋4.5，故当x＝6时，f(x)有最大值4.5，而当x＞7时，f(x)＜10.5－7＝3.5，所以当工厂生产600台产品时盈利最大.

(1)求利润函数f(x)⇒解不等式f(x)>0⇒回答实际问题．

(2)根据第(1)题所求范围，分类讨论求函数最值⇒回答实际问题．

方法归纳

解不等式应用题的四步骤

(1)审：认真审题，把握问题中的关键量，找准不等关系．

(2)设：引进数学符号，用不等式表示不等关系．

(3)求：解不等式．

(4)答：回答实际问题．

特别提醒：确定答案时应注意变量具有的“实际含义”．

跟踪训练4　某农贸公司按每担200元收购某农产品，并按每100元纳税10元(又称征税率为10个百分点)，计划可收购a万担，政府为了鼓励收购公司多收购这种农产品，决定将征税率降低x(x≠0)个百分点，预测收购量可增加2x个百分点．

(1)写出税收y(万元)与x的函数关系式；

(2)要使此项税收在税率调节后，不少于原计划税收的83.2%，试确定x的取值范围．

解析：(1)降低税率后的税率为(10－x)%，农产品的收购量为a(1＋2x%)万担，收购总金额为200a(1＋2x%)

依题意得，y＝200a(1＋2x%)(10－x)%

＝a(100＋2x)(10－x)(0<x<10)．

(2)原计划税收为200a·10%＝20a(万元)．

依题意得，a(100＋2x)(10－x)≥20a×83.2%，

化简得x2＋40x－84≤0，

∴－42≤x≤2.

又∵0＜x＜10，∴0＜x≤2.

∴x的取值范围是{x|0＜x≤2}．

　根据题意，列出各数量之间的关系表，如下：

课时作业 12

一、选择题

1．不等式3x2－2x＋1>0的解集为(　　)

A.  B.

C．∅           D．R

解析：因为Δ＝(－2)2－4×3×1＝－8<0，所以抛物线y＝3x2－2x＋1开口向上，与x轴无交点，故3x2－2x＋1>0恒成立，即不等式3x2－2x＋1>0的解集为R.

答案：D

2．设m＋n>0，则关于x的不等式(m－x)(n＋x)>0的解集是(　　)

A．{x|x<－n或x>m}  B．{x|－n<x<m}

C．{x|x<－m或x>n}  D．{x|－m<x<n}

解析：不等式(m－x)(n＋x)>0可化为(x－m)(x＋n)<0，方程(x－m)(x＋n)＝0的两根为x1＝m，x2＝－n.由m＋n>0，得m>－n，则不等式(x－m)(x＋n)<0的解集是{x|－n<x<m}，故选B.

答案：B

3．不等式ax2＋5x＋c>0的解集为，则a，c的值分别为(　　)

A．a＝6，c＝1  B．a＝－6，c＝－1

C．a＝1，c＝1  D．a＝－1，c＝－6

解析：由题意知，方程ax2＋5x＋c＝0的两根为x1＝，x2＝，由根与系数的关系得x1＋x2＝＋＝－，x1·x2＝×＝.解得a＝－6，c＝－1.

答案：B

4．若不等式x2＋mx＋>0的解集为R，则实数m的取值范围是(　　)

A．(2，＋∞)             B．(－∞，2)

C．(－∞，0)∪(2，＋∞)  D．(0,2)

解析：由题意知原不等式对应方程的Δ<0，即m2－4×1×<0，即m2－2m<0，解得0<m<2，故答案为D.

答案：D

二、填空题

5．不等式(2x－5)(x＋3)<0的解集为________．

解析：方程(2x－5)(x＋3)＝0的两根为x1＝，x2＝－3，函数y＝(2x－5)(x＋3)的图像与x轴的交点坐标为(－3,0)和，所以不等式(2x－5)(x＋3)<0的解集为.

答案：

6．不等式<0的解集为________．

解析：原不等式可以化为(2x－1)(2x＋1)<0，

即<0，

故原不等式的解集为.

答案：

7．用一根长为100 m的绳子能围成一个面积大于600 m2的矩形吗？若“能”，当长＝________ m，宽＝________ m时，所围成的矩形的面积最大．

解析：设矩形一边的长为x m，则另一边的长为(50－x)m,0<x<50.由题意，得x(50－x)>600，即x2－50x＋600<0，解得20<x<30.所以，当矩形一边的长在(20,30)的范围内取值时，能围成一个面积大于600 m2的矩形．用S表示矩形的面积，则S＝x(50－x)＝－(x－25)2＋625(0<x<50)．当x＝25时，S取得最大值，此时50－x＝25.即当矩形的长、宽都为25 m时，所围成的矩形的面积最大．

答案：25　25

三、解答题

8．解下列不等式：

(1)x2＋2x－15>0；

(2)x2－3x＋5>0；

(3)4(2x2－2x＋1)>x(4－x)．

解析：(1)x2＋2x－15>0⇔(x＋5)(x－3)>0⇔x<－5或x>3，所以不等式的解集是{x|x<－5或x>3}．

(2)因为Δ＝(－3)2－4×1×5＝－11<0，再根据函数y＝x2－3x＋5图像的开口方向，所以原不等式的解集为R.

(3)由原不等式得8x2－8x＋4>4x－x2.

∴原不等式等价于9x2－12x＋4>0.

解方程9x2－12x＋4＝0，得x1＝x2＝.

结合二次函数y＝9x2－12x＋4的图像知，原不等式的解集为.

9．若关于x的一元二次不等式ax2＋bx＋c<0的解集为，求关于x的不等式cx2－bx＋a>0的解集．

解析：由题意知所以

代入不等式cx2－bx＋a>0中得ax2＋ax＋a>0(a<0)．

即x2＋x＋1<0，化简得x2＋5x＋6<0，

所以所求不等式的解集为{x|－3<x<－2}．

[尖子生题库]

10．解关于x的不等式x2－ax－2a2<0.

解析：方程x2－ax－2a2＝0的判断式Δ＝a2＋8a2＝9a2≥0，得方程两根x1＝2a，x2＝－a.

(1)若a>0，则－a<x<2a，此时不等式的解集为{x|－a<x<2a}；

(2)若a<0，则2a<x<－a，此时不等式的解集为{x|2a<x<－a}；

(3)若a＝0，则原不等式即为x2<0，此时解集为∅.

综上所述，原不等式的解集为：

当a>0时，{x|－a<x<2a}；

当a<0时，{x|2a<x<－a}；

当a＝0时，∅.