数学必修 第一册1.2.3 充分条件、必要条件学案

这是一份数学必修 第一册1.2.3 充分条件、必要条件学案，共8页。
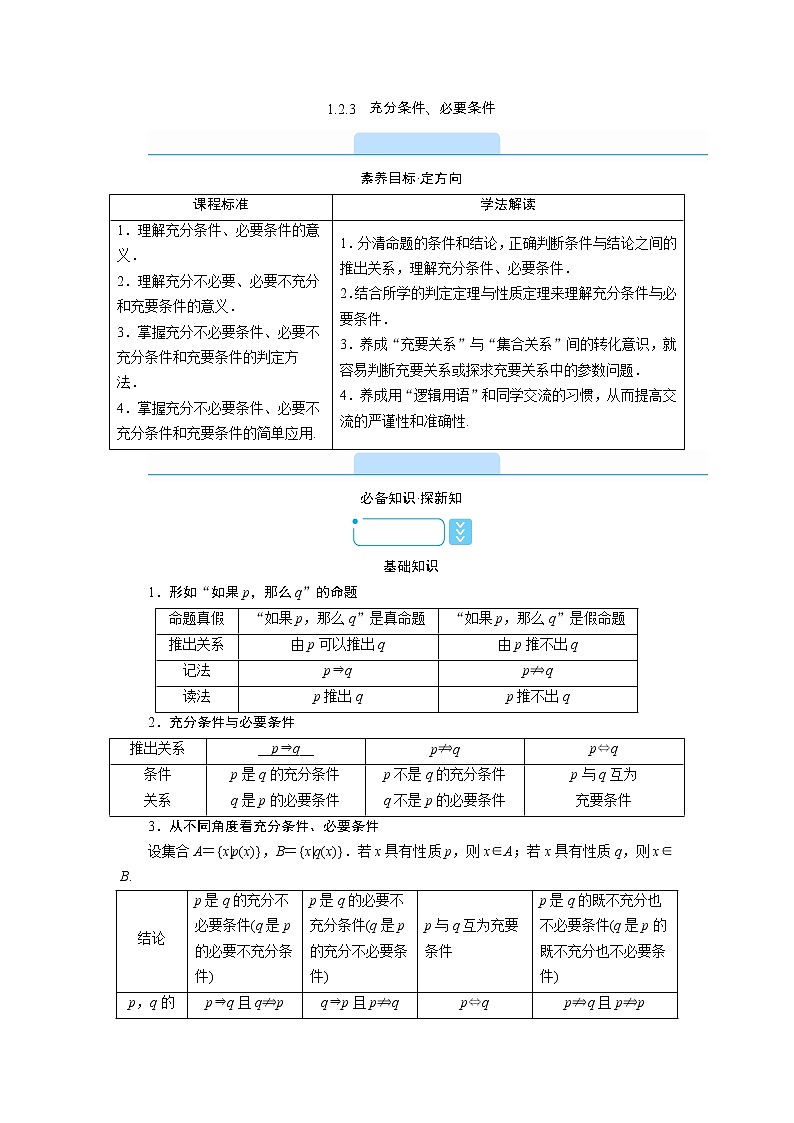
1.2.3　充分条件、必要条件

素养目标·定方向
课程标准
学法解读
1．理解充分条件、必要条件的意义．
2．理解充分不必要、必要不充分和充要条件的意义．
3．掌握充分不必要条件、必要不充分条件和充要条件的判定方法．
4．掌握充分不必要条件、必要不充分条件和充要条件的简单应用.
1．分清命题的条件和结论，正确判断条件与结论之间的推出关系，理解充分条件、必要条件．
2．结合所学的判定定理与性质定理来理解充分条件与必要条件．
3．养成“充要关系”与“集合关系”间的转化意识，就容易判断充要关系或探求充要关系中的参数问题．
4．养成用“逻辑用语”和同学交流的习惯，从而提高交流的严谨性和准确性.

必备知识·探新知

基础知识　　
1．形如“如果p，那么q”的命题
命题真假
“如果p，那么q”是真命题
“如果p，那么q”是假命题
推出关系
由p可以推出q
由p推不出q
记法
p⇒q
pq
读法
p推出q
p推不出q
2．充分条件与必要条件
推出关系
__p⇒q__
pq
p⇔q
条件
关系
p是q的充分条件
q是p的必要条件
p不是q的充分条件
q不是p的必要条件
p与q互为
充要条件
3．从不同角度看充分条件、必要条件
设集合A＝{x|p(x)}，B＝{x|q(x)}．若x具有性质p，则x∈A；若x具有性质q，则x∈B.
结论
p是q的充分不必要条件(q是p的必要不充分条件)
p是q的必要不充分条件(q是p的充分不必要条件)
p与q互为充要条件
p是q的既不充分也不必要条件(q是p的既不充分也不必要条件)
p，q的
关系
p⇒q且qp
q⇒p且pq
p⇔q
pq且pp
集合
AB
BA
A＝B
AB且BA




命题
真假
“若p，则q”是真命题，且“若q，则p”是假命题
“若p，则q”是假命题，且“若q，则p”是真命题
“若p，则q”是真命题，且“若q，则p”是真命题
“若p，则q”是假命题，且“若q，则p”是假命题
思考：用定义法判断充分条件和必要条件的一般步骤是什么？
提示：(1)判定“若p，则q”的真假．
(2)尝试从条件推结论，若条件能推出结论，则条件为充分条件，否则就不是充分条件．
(3)尝试从结论推条件，若结论能推出条件，则条件为必要条件，否则就不是必要条件．

基础自测　　
1．“a＋b