




初中数学人教版七年级下册6.1 平方根图文课件ppt
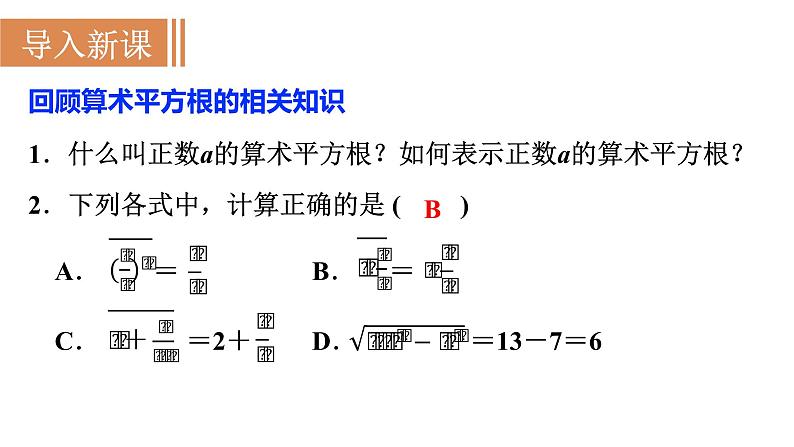
展开回顾算术平方根的相关知识
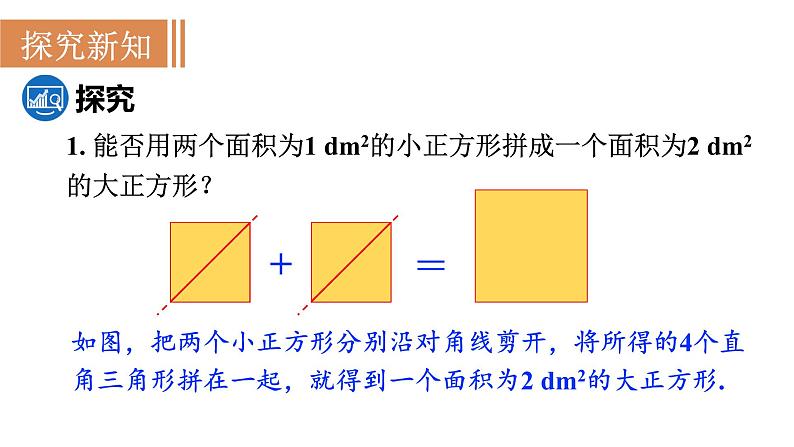
1. 能否用两个面积为1 dm2的小正方形拼成一个面积为2 dm2的大正方形?
如图,把两个小正方形分别沿对角线剪开,将所得的4个直角三角形拼在一起,就得到一个面积为2 dm2的大正方形.
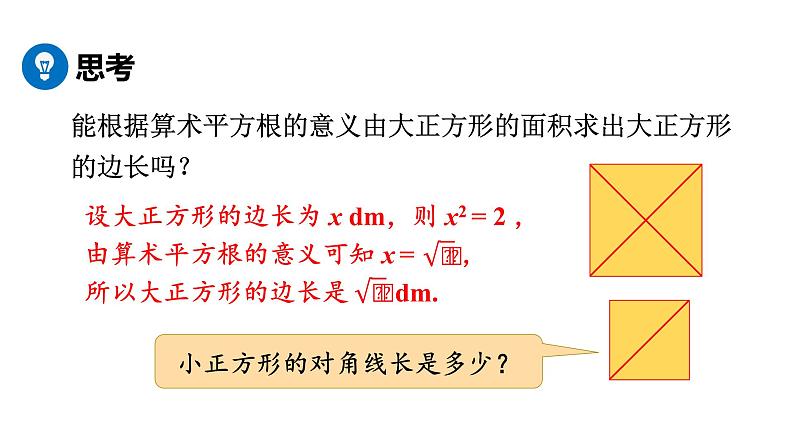
能根据算术平方根的意义由大正方形的面积求出大正方形的边长吗?
设大正方形的边长为 x dm,则 x2 = 2 ,由算术平方根的意义可知 x = , 所以大正方形的边长是 dm.
2. 有多大呢?能不能得到 的更精确的范围?
思考:你是怎样判断出 大于 1 而小于 2 的?
因为12 = 1,22 = 4,而 1 < 2 < 4,所以 1 < < 2.
①∵1.42 = 1.96,1.52 = 2.25,而 1.96 < 2 < 2.25, ∴1.4 < < 1.5.②∵1.412 = 1.9881,1.422 = 2.0164, 而 1.9881 < 2 < 2.0164, ∴1.41 < < 1.42.③∵1.4142 = 1.999396,1.4152 = 2.002225, 而 1.999396 < 2 < 2.002225, ∴1.414 < < 1.415.
用夹逼法求一个数的算术平方根的近似值
估算:在确定一个正数的算术平方根时,可以通过每次增加一位小数计算平方与被开方数比较大小,如此进行下去,在精确度范围内逐步确定出正数的算术平方根的取值范围,这种方法叫做夹逼法.
①∵12=1,22=4,∴1< <2.②∵1.72=2.89,1.82=3.24,∴1.7< <1.8.③∵1.732=2.9929,1.742=3.0276, ∴1.73< <1.74.④∵1.7322=2.999824,1.7332=3.003289, ∴1.732< <1.733, ∴ ≈1.73.
估计一个有理数的算术平方根的近似值,必须先判断这个有理数位于哪两个数的平方之间.比较数的大小,先估计其算术平方根的近似值.
例3 小丽想用一块面积为400 cm2的正方形纸片,沿着边的方向裁出一块面积为300 cm2的长方形纸片,使它的长宽之比为3:2.她不知能否裁得出来,正在发愁.你能帮小丽算出她能用这块纸片裁出符合要求的纸片吗?
解:由题意知正方形纸片的边长为20 cm.
设长方形的长为3x cm,则宽为2x cm,则有
3x·2x=300, x2=50, x= .
∵50>49, ∴ >7, ∴3 >21,
∴小丽不能裁出符合要求的纸片.
∴长方形的长为 3x=3 .
1.实数 的值在( ) A.0 和 1 之间 B.1 和 2 之间 C.2 和 3 之间 D.3 和 4 之间2.与 1 + 最接近的整数是( ) A.1 B.2 C.3 D.4
用计算器求一个数的算术平方根
在估计有理数的算术平方根的过程中,为方便计算,可借助计算器求一个正有理数a的算术平方根(或其近似数).
注意:不同的计算器的按键方式可能有所差别!
利用计算器计算下表中的算术平方根,并将计算结果填在表中,你发现了什么规律?你能说出其中的道理吗?
规律:被开方数的小数点向右每移动____位,它的算术平方根的小数点就向右移动____位;被开方数的小数点向左每移动____位,它的算术平方根的小数点就向左移动____位.
被开方数的小数点向左或向右移动 2n 位时立方根的小数点就相应的向左或向右移动 n 位(n 为正整数).
显示:1.732 050 808
解:∵1 < < 2,∴3 < 2+ < 4, ∴a = 2 + – 3 = – 1, ∵1 < < 2,∴3 < 5 – < 4, ∴b = 5 – – 3 = 2 – , ∴a + b = – 1 + 2 – = 1.
初中数学人教版七年级下册6.1 平方根获奖ppt课件: 这是一份初中数学人教版七年级下册<a href="/sx/tb_c77684_t3/?tag_id=26" target="_blank">6.1 平方根获奖ppt课件</a>,共32页。PPT课件主要包含了a2+1,温故知新,素养目标,课堂导入,新知探究,x22,探究2,你发现了什么规律,探究3,跟踪练习等内容,欢迎下载使用。
初中数学人教版七年级下册6.1 平方根优质ppt课件: 这是一份初中数学人教版七年级下册6.1 平方根优质ppt课件,共23页。PPT课件主要包含了CONTENTS,学习目标,知识回顾,算术平方根,新课导入,探究新知,课堂小结,课堂练习等内容,欢迎下载使用。
初中数学人教版七年级下册6.1 平方根完美版ppt课件: 这是一份初中数学人教版七年级下册6.1 平方根完美版ppt课件,共32页。PPT课件主要包含了学习目标,新课教学,a2+1,x22,小试牛刀,确定整数部分为2,确定十分位为2,你发现了什么规律,课堂小结,比较大小等内容,欢迎下载使用。













